👨🏫🥰🥳需要机械臂相关资源的同学可以在我的CSDN主页中寻找哦🤖😽🦄
指南目录📖:
🎉🎉机械臂速成小指南(零点五):机械臂相关资源🎉🎉
机械臂速成小指南(零):指南主要内容及分析方法
机械臂速成小指南(一):机械臂发展概况
机械臂速成小指南(二):机械臂的应用
机械臂速成小指南(三):机械臂的机械结构
机械臂速成小指南(四):机械臂关键部件之减速机
机械臂速成小指南(五):末端执行器
机械臂速成小指南(六):步进电机驱动器
机械臂速成小指南(七):机械臂位姿的描述方法
机械臂速成小指南(八):运动学建模(标准DH法)
机械臂速成小指南(九):正运动学分析
机械臂速成小指南(十):可达工作空间
机械臂速成小指南(十一):坐标系的标准命名
机械臂速成小指南(十二):逆运动学分析
机械臂速成小指南(十三):轨迹规划概述
机械臂速成小指南(十四):多项式插值轨迹规划
机械臂速成小指南(十五):线性规划
机械臂速成小指南(十六):带抛物线过渡的线性规划
机械臂速成小指南(十七):直线规划
机械臂速成小指南(十八):圆弧规划
机械臂速成小指南(十九):机械臂的电路板抓取实验
机械臂速成小指南(二十):机械臂的位姿重复性实验
机械臂速成小指南(二十一):几何雅可比矩阵
机械臂速成小指南(二十二):机械臂逆运动学的数值解方法
机械臂速成小指南(二十三):Paul方法求解机械臂运动学逆解(含matlab代码)
🦾🌏🪐以下为正文🦾🌏🪐
六自由度机械臂上位机python代码(带详细注释,含正逆运动学及轨迹规划代码)
在第八章中,我们已经得到了所使用机械臂的DH参数,如下表所示:
| 连杆编号 |  |
 |
 |
 |
关节变量范围 |
| 1 | 64.2 | -90 | 169.77 | θ1 | (-170,+170) |
| 2 | 305 | 0 | 0 | θ2 | (-132,0) |
| 3 | 0 | 90 | 0 | θ3 | (1,141) |
| 4 | 0 | -90 | -222.63 | θ4 | (-165,+ 165) |
| 5 | 0 | 90 | 0 | θ5 | (-105,+105) |
| 6 | 0 | 0 | -36.25 | θ6 | (-155,+155) |
在确定机械臂的DH参数后,使用齐次变换矩阵描述各坐标系之间的旋转、平移关系,并利用齐次变换矩阵构建机械臂的正运动学方程,以此对六自由度机械臂展开正运动学分析。
一、构建机械臂的正运动学方程
从坐标系i到坐标系i-1 的齐次变换矩阵 是一个仅与关节变量
是一个仅与关节变量 有关的函数,本文记为
有关的函数,本文记为 。下面列出推导
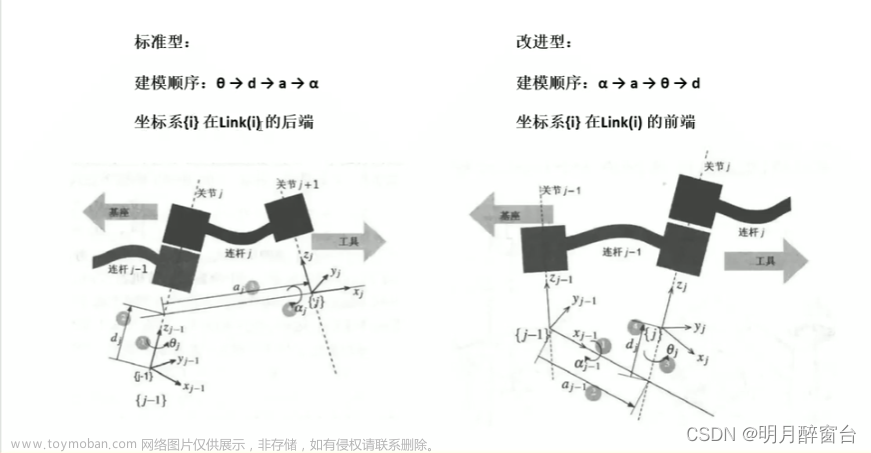
。下面列出推导 的过程,以坐标系i与坐标系i-1 为例,坐标变换坐标系的旋转、平移过程如下图所示。
的过程,以坐标系i与坐标系i-1 为例,坐标变换坐标系的旋转、平移过程如下图所示。

首先,设一坐标系k 与坐标系i-1 排列一致,然后将坐标系k 沿轴zi-1 平移di
平移di 并绕轴zi-1
并绕轴zi-1 旋转θi
旋转θi 。此时坐标系k 已与坐标系
。此时坐标系k 已与坐标系 排列一致,该过程可用齐次变换矩阵描述为
排列一致,该过程可用齐次变换矩阵描述为

式中 表示cos(n) ,
表示cos(n) , 表示sin(n) ,计算时需考虑到两个坐标系的x 轴之间初始的夹角θ 。
表示sin(n) ,计算时需考虑到两个坐标系的x 轴之间初始的夹角θ 。
接着,将坐标系k 沿轴xi' 平移
平移 并绕其旋转
并绕其旋转 ,这使得坐标系与坐标系i 排列一致,该过程可用齐次变换矩阵描述为
,这使得坐标系与坐标系i 排列一致,该过程可用齐次变换矩阵描述为

从坐标系i 到坐标系i-1 的齐次变换矩阵可通过右乘单一变换矩阵 及
及 得出,为
得出,为

根据上式可得出表示各坐标系间相对位置和方向的齐次变换矩阵,将其看作各关节的齐次变换矩阵,计算结果如下表所示。
| 关节编号 | 齐次变换矩阵 |
| 1 |  |
| 2 |  |
| 3 |  |
| 4 |  |
| 5 |  |
| 6 |  |
由于坐标系0与基坐标系重合,又由于坐标系6即为工具坐标系,所以有

则用于表示工具坐标系相对于基坐标系的正运动学方程可以由上表中6个齐次变换矩阵右乘得出,为

前三个关节组成拟人臂,则其正运动学方程表示为

其中, 及
及 分别表示sin(qj+…+qk) 和cos(qj+…+qk) 。
分别表示sin(qj+…+qk) 和cos(qj+…+qk) 。
后三个关节组成球形腕,同理可得,球型腕的正运动学方程可表示为

进而可以得出机械臂的正运动学方程为:

其中, 为关节变量组成的向量,向量q的空间称为关节空间。
为关节变量组成的向量,向量q的空间称为关节空间。
经计算,末端执行器的位置表示为

同理,可得到末端执行器的姿态表示为



最终,末端执行器的RPY角可表示为关于关节变量的超越函数,即



至此,机械臂的正运动学公式求解完毕,当我们将关节变量代入公式即可得到末端执行器的位姿。
二、正运动学方程求解的编程实现
由于正运动学方程运算量较大,为提高运算速度,我们选择使用上位机完成运算。使用Python编写机械臂正运动方程求解函数CalcFwdKin(),输入参数为6个关节变量,输出为末端执行器的位置与姿态。
机械臂的正运动学方程是关节变量的超越函数,求解过程中存在大量的三角函数计算及矩阵运算,因此我们引入Python自带的math标准库,该模块提供了许多对浮点数的数学运算函数。

在求解正运动学方程的过程中使用math.sin()、math.cos()及math.atan2()完成三角函数的计算;使用math.sqrt()求取平方根;通过math.degrees()及math.radians()完成弧度与角度之间的转换。
要使用 math 函数必须先导入:
import math 文章来源:https://www.toymoban.com/news/detail-417671.html
文章来源:https://www.toymoban.com/news/detail-417671.html
效果如下图所示: 文章来源地址https://www.toymoban.com/news/detail-417671.html
文章来源地址https://www.toymoban.com/news/detail-417671.html
############## DH TABLE ################
############## DH 参数表 ###############
C13 = C4
C14 = C5
C15 = C6
C16 = C7
C17 = C8
C18 = C9
D13 = math.radians(DHr1)
D14 = math.radians(DHr2)
D15 = math.radians(DHr3)
D16 = math.radians(DHr4)
D17 = math.radians(DHr5)
D18 = math.radians(DHr6)
E13 = DHd1
E14 = DHd2
E15 = DHd3
E16 = DHd4
E17 = DHd5
E18 = DHd6
F13 = DHa1
F14 = DHa2
F15 = DHa3
F16 = DHa4
F17 = DHa5
F18 = DHa6
## WORK FRAME INPUT
H13 = float(UFxEntryField.get())
H14 = float(UFyEntryField.get())
H15 = float(UFzEntryField.get())
H16 = float(UFrxEntryField.get())
H17 = float(UFryEntryField.get())
H18 = float(UFrzEntryField.get())
## TOOL FRAME INPUT
J13 = float(TFxEntryField.get())
J14 = float(TFyEntryField.get())
J15 = float(TFzEntryField.get())
J16 = float(TFrxEntryField.get())
J17 = float(TFryEntryField.get())
J18 = float(TFrzEntryField.get())
## WORK FRAME TABLE
B21 = math.cos(math.radians(H18))*math.cos(math.radians(H17))
B22 = math.sin(math.radians(H18))*math.cos(math.radians(H17))
B23 = -math.sin(math.radians(H18))
B24 = 0
C21 = -math.sin(math.radians(H18))*math.cos(math.radians(H16))+math.cos(math.radians(H18))*math.sin(math.radians(H17))*math.sin(math.radians(H16))
C22 = math.cos(math.radians(H18))*math.cos(math.radians(H16))+math.sin(math.radians(H18))*math.sin(math.radians(H17))*math.sin(math.radians(H16))
C23 = math.cos(math.radians(H17))*math.sin(math.radians(H16))
C24 = 0
D21 = math.sin(math.radians(H18))*math.sin(math.radians(H16))+math.cos(math.radians(H18))*math.sin(math.radians(H17))*math.cos(math.radians(H16))
D22 = -math.cos(math.radians(H18))*math.sin(math.radians(H16))+math.sin(math.radians(H18))*math.sin(math.radians(H17))*math.cos(math.radians(H16))
D23 = math.cos(math.radians(H17))*math.cos(math.radians(H16))
D24 = 0
E21 = H13
E22 = H14
E23 = H15
E24 = 1
## J1 FRAME
B27 = math.cos(C13)
B28 = math.sin(C13)
B29 = 0
B30 = 0
C27 = -math.sin(C13)*math.cos(D13)
C28 = math.cos(C13)*math.cos(D13)
C29 = math.sin(D13)
C30 = 0
D27 = math.sin(C13)*math.sin(D13)
D28 = -math.cos(C13)*math.sin(D13)
D29 = math.cos(D13)
D30 = 0
E27 = F13*math.cos(C13)
E28 = F13*math.sin(C13)
E29 = E13
E30 = 1
## J2 FRAME
B33 = math.cos(C14)
B34 = math.sin(C14)
B35 = 0
B36 = 0
C33 = -math.sin(C14)*math.cos(D14)
C34 = math.cos(C14)*math.cos(D14)
C35 = math.sin(D14)
C36 = 0
D33 = math.sin(C14)*math.sin(D14)
D34 = -math.cos(C14)*math.sin(D14)
D35 = math.cos(D14)
D36 = 0
E33 = F14*math.cos(C14)
E34 = F14*math.sin(C14)
E35 = E14
E36 = 1
## J3 FRAME
B39 = math.cos(C15)
B40 = math.sin(C15)
B41 = 0
B42 = 0
C39 = -math.sin(C15)*math.cos(D15)
C40 = math.cos(C15)*math.cos(D15)
C41 = math.sin(D15)
C42 = 0
D39 = math.sin(C15)*math.sin(D15)
D40 = -math.cos(C15)*math.sin(D15)
D41 = math.cos(D15)
D42 = 0
E39 = F15*math.cos(C15)
E40 = F15*math.sin(C15)
E41 = 0
E42 = 1
## J4 FRAME
B45 = math.cos(C16)
B46 = math.sin(C16)
B47 = 0
B48 = 0
C45 = -math.sin(C16)*math.cos(D16)
C46 = math.cos(C16)*math.cos(D16)
C47 = math.sin(D16)
C48 = 0
D45 = math.sin(C16)*math.sin(D16)
D46 = -math.cos(C16)*math.sin(D16)
D47 = math.cos(D16)
D48 = 0
E45 = F16*math.cos(C16)
E46 = F16*math.sin(C16)
E47 = E16
E48 = 1
## J5 FRAME
B51 = math.cos(C17)
B52 = math.sin(C17)
B53 = 0
B54 = 0
C51 = -math.sin(C17)*math.cos(D17)
C52 = math.cos(C17)*math.cos(D17)
C53 = math.sin(D17)
C54 = 0
D51 = math.sin(C17)*math.sin(D17)
D52 = -math.cos(C17)*math.sin(D17)
D53 = math.cos(D17)
D54 = 0
E51 = F17*math.cos(C17)
E52 = F17*math.sin(C17)
E53 = E17
E54 = 1
## J6 FRAME
B57 = math.cos(C18)
B58 = math.sin(C18)
B59 = 0
B60 = 0
C57 = -math.sin(C18)*math.cos(D18)
C58 = math.cos(C18)*math.cos(D18)
C59 = math.sin(D18)
C60 = 0
D57 = math.sin(C18)*math.sin(D18)
D58 = -math.cos(C18)*math.sin(D18)
D59 = math.cos(D18)
D60 = 0
E57 = F18*math.cos(C18)
E58 = F18*math.sin(C18)
E59 = E18
E60 = 1
###################### TOOL FRAME ###########################
###################### 工具坐标系 ############################
B63 = math.cos(math.radians(J18))*math.cos(math.radians(J17))
B64 = math.sin(math.radians(J18))*math.cos(math.radians(J17))
B65 = -math.sin(math.radians(J18))
B66 = 0
C63 = -math.sin(math.radians(J18))*math.cos(math.radians(J16))+math.cos(math.radians(J18))*math.sin(math.radians(J17))*math.sin(math.radians(J16))
C64 = math.cos(math.radians(J18))*math.cos(math.radians(J16))+math.sin(math.radians(J18))*math.sin(math.radians(J17))*math.sin(math.radians(J16))
C65 = math.cos(math.radians(J17))*math.sin(math.radians(J16))
C66 = 0
D63 = math.sin(math.radians(J18))*math.sin(math.radians(J16))+math.cos(math.radians(J18))*math.sin(math.radians(J17))*math.cos(math.radians(J16))
D64 = -math.cos(math.radians(J18))*math.sin(math.radians(J16))+math.sin(math.radians(J18))*math.sin(math.radians(J17))*math.cos(math.radians(J16))
D65 = math.cos(math.radians(J17))*math.cos(math.radians(J16))
D66 = 0
E63 = J13
E64 = J14
E65 = J15
E66 = 1
## WF*J1
G24 = (B21*B27)+(C21*B28)+(D21*B29)+(E21*B30)
G25 = (B22*B27)+(C22*B28)+(D22*B29)+(E22*B30)
G26 = (B23*B27)+(C23*B28)+(D23*B29)+(E23*B30)
G27 = (B24*B27)+(C24*B28)+(D24*B29)+(E24*B30)
H24 = (B21*C27)+(C21*C28)+(D21*C29)+(E21*C30)
H25 = (B22*C27)+(C22*C28)+(D22*C29)+(E22*C30)
H26 = (B23*C27)+(C23*C28)+(D23*C29)+(E23*C30)
H27 = (B24*C27)+(C24*C28)+(D24*C29)+(E24*C30)
I24 = (B21*D27)+(C21*D28)+(D21*D29)+(E21*D30)
I25 = (B22*D27)+(C22*D28)+(D22*D29)+(E22*D30)
I26 = (B23*D27)+(C23*D28)+(D23*D29)+(E23*D30)
I27 = (B24*D27)+(C24*D28)+(D24*D29)+(E24*D30)
J24 = (B21*E27)+(C21*E28)+(D21*E29)+(E21*E30)
J25 = (B22*E27)+(C22*E28)+(D22*E29)+(E22*E30)
J26 = (B23*E27)+(C23*E28)+(D23*E29)+(E23*E30)
J27 = (B24*E27)+(C24*E28)+(D24*E29)+(E24*E30)
## (WF*J1)*J2
G30 = (G24*B33)+(H24*B34)+(I24*B35)+(J24*B36)
G31 = (G25*B33)+(H25*B34)+(I25*B35)+(J25*B36)
G32 = (G26*B33)+(H26*B34)+(I26*B35)+(J26*B36)
G33 = (G27*B33)+(H27*B34)+(I27*B35)+(J27*B36)
H30 = (G24*C33)+(H24*C34)+(I24*C35)+(J24*C36)
H31 = (G25*C33)+(H25*C34)+(I25*C35)+(J25*C36)
H32 = (G26*C33)+(H26*C34)+(I26*C35)+(J26*C36)
H33 = (G27*C33)+(H27*C34)+(I27*C35)+(J27*C36)
I30 = (G24*D33)+(H24*D34)+(I24*D35)+(J24*D36)
I31 = (G25*D33)+(H25*D34)+(I25*D35)+(J25*D36)
I32 = (G26*D33)+(H26*D34)+(I26*D35)+(J26*D36)
I33 = (G27*D33)+(H27*D34)+(I27*D35)+(J27*D36)
J30 = (G24*E33)+(H24*E34)+(I24*E35)+(J24*E36)
J31 = (G25*E33)+(H25*E34)+(I25*E35)+(J25*E36)
J32 = (G26*E33)+(H26*E34)+(I26*E35)+(J26*E36)
J33 = (G27*E33)+(H27*E34)+(I27*E35)+(J27*E36)
## (WF*J1*J2)*J3
G36 = (G30*B39)+(H30*B40)+(I30*B41)+(J30*B42)
G37 = (G31*B39)+(H31*B40)+(I31*B41)+(J31*B42)
G38 = (G32*B39)+(H32*B40)+(I32*B41)+(J32*B42)
G39 = (G33*B39)+(H33*B40)+(I33*B41)+(J33*B42)
H36 = (G30*C39)+(H30*C40)+(I30*C41)+(J30*C42)
H37 = (G31*C39)+(H31*C40)+(I31*C41)+(J31*C42)
H38 = (G32*C39)+(H32*C40)+(I32*C41)+(J32*C42)
H39 = (G33*C39)+(H33*C40)+(I33*C41)+(J33*C42)
I36 = (G30*D39)+(H30*D40)+(I30*D41)+(J30*D42)
I37 = (G31*D39)+(H31*D40)+(I31*D41)+(J31*D42)
I38 = (G32*D39)+(H32*D40)+(I32*D41)+(J32*D42)
I39 = (G33*D39)+(H33*D40)+(I33*D41)+(J33*D42)
J36 = (G30*E39)+(H30*E40)+(I30*E41)+(J30*E42)
J37 = (G31*E39)+(H31*E40)+(I31*E41)+(J31*E42)
J38 = (G32*E39)+(H32*E40)+(I32*E41)+(J32*E42)
J39 = (G33*E39)+(H33*E40)+(I33*E41)+(J33*E42)
## (WF*J1*J2*J3)*J4
G42 = (G36*B45)+(H36*B46)+(I36*B47)+(J36*B48)
G43 = (G37*B45)+(H37*B46)+(I37*B47)+(J37*B48)
G44 = (G38*B45)+(H38*B46)+(I38*B47)+(J38*B48)
G45 = (G39*B45)+(H39*B46)+(I39*B47)+(J39*B48)
H42 = (G36*C45)+(H36*C46)+(I36*C47)+(J36*C48)
H43 = (G37*C45)+(H37*C46)+(I37*C47)+(J37*C48)
H44 = (G38*C45)+(H38*C46)+(I38*C47)+(J38*C48)
H45 = (G39*C45)+(H39*C46)+(I39*C47)+(J39*C48)
I42 = (G36*D45)+(H36*D46)+(I36*D47)+(J36*D48)
I43 = (G37*D45)+(H37*D46)+(I37*D47)+(J37*D48)
I44 = (G38*D45)+(H38*D46)+(I38*D47)+(J38*D48)
I45 = (G39*D45)+(H39*D46)+(I39*D47)+(J39*D48)
J42 = (G36*E45)+(H36*E46)+(I36*E47)+(J36*E48)
J43 = (G37*E45)+(H37*E46)+(I37*E47)+(J37*E48)
J44 = (G38*E45)+(H38*E46)+(I38*E47)+(J38*E48)
J45 = (G39*E45)+(H39*E46)+(I39*E47)+(J39*E48)
## (WF*J1*J2*J3*J4)*J5
G48 = (G42*B51)+(H42*B52)+(I42*B53)+(J42*B54)
G49 = (G43*B51)+(H43*B52)+(I43*B53)+(J43*B54)
G50 = (G44*B51)+(H44*B52)+(I44*B53)+(J44*B54)
G51 = (G45*B51)+(H45*B52)+(I45*B53)+(J45*B54)
H48 = (G42*C51)+(H42*C52)+(I42*C53)+(J42*C54)
H49 = (G43*C51)+(H43*C52)+(I43*C53)+(J43*C54)
H50 = (G44*C51)+(H44*C52)+(I44*C53)+(J44*C54)
H51 = (G45*C51)+(H45*C52)+(I45*C53)+(J45*C54)
I48 = (G42*D51)+(H42*D52)+(I42*D53)+(J42*D54)
I49 = (G43*D51)+(H43*D52)+(I43*D53)+(J43*D54)
I50 = (G44*D51)+(H44*D52)+(I44*D53)+(J44*D54)
I51 = (G45*D51)+(H45*D52)+(I45*D53)+(J45*D54)
J48 = (G42*E51)+(H42*E52)+(I42*E53)+(J42*E54)
J49 = (G43*E51)+(H43*E52)+(I43*E53)+(J43*E54)
J50 = (G44*E51)+(H44*E52)+(I44*E53)+(J44*E54)
J51 = (G45*E51)+(H45*E52)+(I45*E53)+(J45*E54)
## (WF*J1*J2*J3*J4*J5)*J6
G54 = (G48*B57)+(H48*B58)+(I48*B59)+(J48*B60)
G55 = (G49*B57)+(H49*B58)+(I49*B59)+(J49*B60)
G56 = (G50*B57)+(H50*B58)+(I50*B59)+(J50*B60)
G57 = (G51*B57)+(H51*B58)+(I51*B59)+(J51*B60)
H54 = (G48*C57)+(H48*C58)+(I48*C59)+(J48*C60)
H55 = (G49*C57)+(H49*C58)+(I49*C59)+(J49*C60)
H56 = (G50*C57)+(H50*C58)+(I50*C59)+(J50*C60)
H57 = (G51*C57)+(H51*C58)+(I51*C59)+(J51*C60)
I54 = (G48*D57)+(H48*D58)+(I48*D59)+(J48*D60)
I55 = (G49*D57)+(H49*D58)+(I49*D59)+(J49*D60)
I56 = (G50*D57)+(H50*D58)+(I50*D59)+(J50*D60)
I57 = (G51*D57)+(H51*D58)+(I51*D59)+(J51*D60)
J54 = (G48*E57)+(H48*E58)+(I48*E59)+(J48*E60)
J55 = (G49*E57)+(H49*E58)+(I49*E59)+(J49*E60)
J56 = (G50*E57)+(H50*E58)+(I50*E59)+(J50*E60)
J57 = (G51*E57)+(H51*E58)+(I51*E59)+(J51*E60)
## (WF*J1*J2*J3*J4*J5*J6)*TF
G60 = (G54*B63)+(H54*B64)+(I54*B65)+(J54*B66)
G61 = (G55*B63)+(H55*B64)+(I55*B65)+(J55*B66)
G62 = (G56*B63)+(H56*B64)+(I56*B65)+(J56*B66)
G63 = (G57*B63)+(H57*B64)+(I57*B65)+(J57*B66)
H60 = (G54*C63)+(H54*C64)+(I54*C65)+(J54*C66)
H61 = (G55*C63)+(H55*C64)+(I55*C65)+(J55*C66)
H62 = (G56*C63)+(H56*C64)+(I56*C65)+(J56*C66)
H63 = (G57*C63)+(H57*C64)+(I57*C65)+(J57*C66)
I60 = (G54*D63)+(H54*D64)+(I54*D65)+(J54*D66)
I61 = (G55*D63)+(H55*D64)+(I55*D65)+(J55*D66)
I62 = (G56*D63)+(H56*D64)+(I56*D65)+(J56*D66)
I63 = (G57*D63)+(H57*D64)+(I57*D65)+(J57*D66)
J60 = (G54*E63)+(H54*E64)+(I54*E65)+(J54*E66)
J61 = (G55*E63)+(H55*E64)+(I55*E65)+(J55*E66)
J62 = (G56*E63)+(H56*E64)+(I56*E65)+(J56*E66)
J63 = (G57*E63)+(H57*E64)+(I57*E65)+(J57*E66)到了这里,关于机械臂速成小指南(九):正运动学分析的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!