OI 数论中的上界估计与时间复杂度证明-Toy模板网

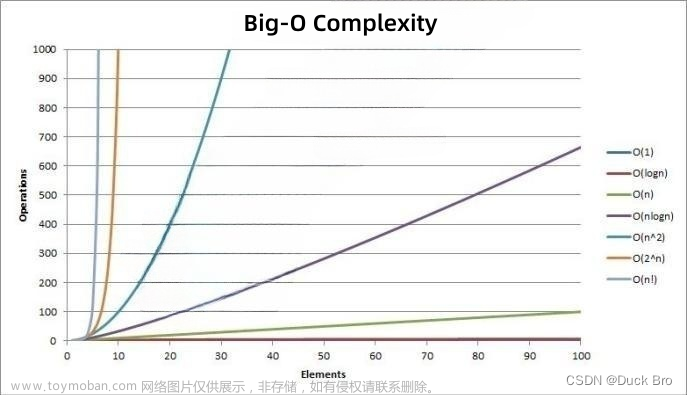
这篇具有很好参考价值的文章主要介绍了OI 数论中的上界估计与时间复杂度证明。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

预备

0.1 渐进符号

其实不少高等数学 / 数学分析教材在讲解无穷小的比较时已经相当严谨地介绍过大 O、小 O 记号，然而各种历史习惯记法的符号滥用（abuse of notation）^[1] 直到现在都让笔者头疼. These notations seem to be innocent, but can be catastrophic without careful manipulation. For example,

$n = O (n^{2}) \land n^{2} = O (n^{2}) ⟹ n = n^{2}$

Knuth 在《具体数学》里举出的例子^[2]. “ $=$ ” 隐含的对称性使其在 $g (x) = O (f (x))$ 中格格不入. 事实上，将 $O (f (x))$ 看作“阶不高于 $f (x)$ 的所有函数的集合”是比“某个阶不高于 $f (x)$ 的函数”更严谨的理解. 因此，本文将使用 $f (x) \in O (g (x))$ （有时也记为 $O (f (x)) \subset O (g (x))$ ）的集合论符号代替传统的 $f (x) = O (g (x))$ 记法.
$n^{2} \sin n \in O (n^{2}) ⟹ \sum_{i = 1}^{n} i^{2} \sin i \in \sum_{i = 1}^{n} O (i^{2}) \subset O (\sum_{i = 1}^{n} i^{2}) \subset O (n^{3})$ 或更一般的， $g (x) \in O (f (x)) ⟹ \sum_{P (n, i)} g (i) \in \sum_{P (n, i)} O (f (i)) \subset O (\sum_{P (n, i)} f (i))$

没看出有啥问题，对吧？笔者在写作此文时犯了同样的错误. 请注意，大 O 记号的作用对象是函数， $f (i)$ 是什么？它只是个函数值，是确定的数——这是因为 $i$ 也是求和枚举中确定的数，而不是 $n$ 这种真正代表变元的记号. 所以 $O (f (i))$ 是什么？它什么也不是.

这种错误的出现是在所难免的，我们太习惯用 $x$ 、 $x^{3} + 5 x^{2} + x$ 这种变元都不明确的记号来表示函数了^[1]. 写成 $f (x)$ 也不严谨，因为只有 $f$ 才应代表函数本身， $f (x)$ 只能是函数值. 这样我们就可以放心地写下 $O (f)$ ，不用担心把变元与确定值弄混了.

然而大家还是喜欢写 $O (n^{2})$ 和 $O (e^{n^{2}})$ ，而不是奇怪的 $O ({id}^{2})$ 和 $O (\exp \circ {id}^{2})$ . 所以，我们大概只能沿用这种不太严谨的记号，并时刻提醒自己加倍小心了. （形如 $x \mapsto e^{x^{2}}$ 的 $λ$ 风格“匿名函数”记号可能更好？）

但上述命题从结论上是正确的. 正确的推导过程应为 $\sum_{P (n, i)} g (i) \leq \sum_{P (n, i)} C f (i) \leq C \sum_{P (n, i)} f (i) \in O (\sum_{P (n, i)} f (i))$

第一步是直接由大 O 记号的定义得到的结果.

Wikipedia^[3] 中有一张详尽的表格介绍了各种渐进符号的定义，OI Wiki^[4] 上也有极好的讲解，尚不熟练的读者可以参考. 有兴趣仔细研究的读者可以参考《具体数学》第九章^[2]、Wikipedia 及其 reference（个人推荐 Knuth 关于 $O$ 、 $Ω$ 、 $Θ$ 的短文^[5]）. 本文除用 “ $\in$ ” 和“ $\subset$ ”替代 “ $=$ ” 外，完全使用 Knuth 提议的记号体系.

0.2 调和数 H(n) / 调和级数

调和级数的部分和 $H (n)$ 定义为 $H (n) = \sum_{i = 1}^{n} \frac{1}{i}$ 通过一些与 $e$ 有关的数列放缩可以证明 $lim_{n \to \infty} (H (n) - \log n) = c$ ，其中 $c \approx 0.577$ 是 Euler 常数. 因此 $n H (n) \sim n \log n \in Θ (\log n)$ .

0.3 自然数等幂和 Pp(n) / p - 级数

$p$ - 级数可视为调和级数的推广. 其部分和定义为 $P_{p} (n) = \sum_{i = 1}^{n} i^{- p}$

$p$ - 级数具有如下性质：

当 $p > 1$ 时， $p$ - 级数收敛；
当 $p = 1$ 时， $p$ - 级数是调和级数；
当 $- \infty < p < 1$ 时，我们指出 $P_{p} (n) \sim \frac{1}{1 - p} n^{1 - p} \in Θ (n^{1 - p})$

$- \infty < p < 1$ 时 $p$ - 级数的渐进估计可以从连续幂函数积分的角度理解. 证明这渐进性，离散情况下，可对 $n^{p}$ 差分后前缀和 + 二项式定理得到高次项系数，或可用离散微积分理论得到精确表示（参见《具体数学》^[6]）；连续情况下，Lagrange 中值定理应为较简单的估计方法. 这里从略. 总之，我们得到： $P_{p} (n) \in {\begin{cases} Θ (n^{1 - p}) & p < 1 \\ Θ (n \log n) & p = 1 \\ Θ (1) & p > 1 \end{cases}$

1 约数函数 σz(n)

约数函数（Divisor Function，也可称为除数函数、因数函数）是与 $n$ 的因子有关的一类函数，定义如下：

Definition 1 (约数函数) $σ_{z} (n) = \sum_{d ∣ n} d^{z}$

当 $z = 0$ 时， $σ_{0} (n)$ 被称为约数个数函数（number-of-divisors function），常被记为 $d (n)$ 或 $τ (n)$ . 当 $z = 1$ 时， $σ_{1} (n)$ 被称为约数和函数（sum-of-divisors function），常直接记为 $σ (n)$ .

Example 1 估计 $σ_{0} (n)$ 的渐进上界.

也就是估计 $n$ 的因子的数量. 一个广为人知的上界是 $2 \sqrt{n}$ ，因为 $n$ 的所有小于 $\sqrt{n}$ 的因子 $d$ 均与另一因子 $\frac{n}{d}$ 一一对应.

事实上进一步可以证明 $σ_{0} (n) \in o (n^{ϵ}) \forall ϵ > 0$ ^[7]，虽然这在 OI 中并不实用.

Example 2 估计 $\hat{σ_{0}} (n) = \sum_{i = 1}^{n} σ_{0} (i)$ 的渐进上界.

即估计 $1$ 到 $n$ 中所有数因子个数的和. 这是一个形式上鲜为人知但其应用广为人知的例子. 变换求和顺序，容易得到

$\hat{σ_{0}} (n) = \sum_{i = 1}^{n} σ_{0} (i) = \sum_{i = 1}^{n} \sum_{d ∣ i} 1 = \sum_{d = 1}^{n} ⌊ \frac{n}{d} ⌋ \leq \sum_{d = 1}^{n} \frac{n}{d} = n H (n) \in O (n \log n)$

显然，这比 $O (n \sqrt{n})$ 的平凡估计好上不少. 本例的思路不仅是埃氏筛（Sieve of Eratosthenes）的理论基础，也在杜教筛、快速 Mobius 变换、 $gcd$ 卷积^[8]等处出现.

进一步利用此技巧和 $p$ - 级数的估计，我们甚至能在仔细研究 $σ_{z} (n)$ 前就得到其前缀和的渐进估计：

Example 3 估计 $\hat{σ_{z}} (n) = \sum_{i = 1}^{n} σ_{z} (i)$ 的渐进上界.

$\begin{aligned} \hat{σ_{z}} (n) & = \sum_{i = 1}^{n} σ_{z} (i) = \sum_{i = 1}^{n} \sum_{d ∣ i} d^{z} = \sum_{d = 1}^{n} d^{z} ⌊ \frac{n}{d} ⌋ \\ \leq n \sum_{d = 1}^{n} d^{z - 1} = n P_{1 - z} (n) \in {\begin{cases} O (n^{z + 1}) & z > 0 \\ O (n \log n) & z = 0 \\ O (n) & z < 0 \end{cases} \end{aligned}$

遗憾的是，对此前缀和做差分并不能得到 $σ_{z} (n)$ 的优秀估计.

现在引入一个重要放缩技巧，其在后续估计中屡试不爽.

Proposition 1 $\sum_{d ∣ n} f (d) \leq \sum_{i = 1}^{n} f (⌊ \frac{n}{i} ⌋)$

显然，右式比左式多算了 $i ∤ n$ 的项，因此命题是正确的. 但我们还可以做得更好：

Proposition 2 $\sum_{d ∣ n} f (d) \leq \sum_{i = 1}^{\sqrt{n}} f (i) + f (⌊ \frac{n}{i} ⌋)$

$\sqrt{n}$ 分治. 我们其实已经在 Example 1 估计 $σ_{0} (n)$ 时用过此技巧了.

Example 4 估计 $σ_{1} (n)$ 的渐进上界.

用 Proposition 1： $σ_{1} (n) = \sum_{d ∣ n} d \leq \sum_{i = 1}^{n} ⌊ \frac{n}{i} ⌋ \leq n H (n) \in O (n \log n)$

可以证明用 Proposition 2 不会得到更优的结果.

我们发现了一个有趣的事实： $σ_{1} (n)$ 和 $\hat{σ_{0}} (n)$ 的渐进上界均为 $O (n \log n)$ .

Example 5 估计 $σ_{z} (n)$ 的渐进上界.

用 Proposition 2 和 $p$ - 级数的性质：

$\begin{aligned} σ_{z} (n) & = \sum_{d ∣ n} d^{z} \leq \sum_{i = 1}^{\sqrt{n}} i^{z} + {⌊ \frac{n}{i} ⌋}^{z} \\ \leq {\begin{cases} 2 \sum_{i = 1}^{\sqrt{n}} {⌊ \frac{n}{i} ⌋}^{z} \leq 2 n^{z} \sum_{i = 1}^{\sqrt{n}} i^{- z} & = 2 n^{z} P_{z} (\sqrt{n}) & z \geq 0 \\ 2 \sum_{i = 1}^{\sqrt{n}} i^{z} & = 2 P_{- z} (\sqrt{n}) & z < 0 \end{cases} \\ \in & {\begin{cases} 2 n^{z} O (1) & z > 1 \\ 2 n O (\log \sqrt{n}) & z = 1 \\ 2 n^{z} O (n^{\frac{1 - z}{2}}) & 0 \leq z < 1 \\ 2 O (n^{\frac{1 + z}{2}}) & - 1 < z < 0 \\ 2 O (\log \sqrt{n}) & z = - 1 \\ 2 O (1) & z < - 1 \end{cases} = {\begin{cases} O (n^{z}) & z > 1 \\ O (n \log n) & z = 1 \\ O (n^{\frac{1 + z}{2}}) & - 1 < z < 1 \\ O (\log n) & z = - 1 \\ O (1) & z < - 1 \end{cases} \end{aligned}$

我们得到了一个相当优秀的渐进上界. 值得关注的是：

当 $z = 0$ 时， $σ_{0} (n) \in O (n^{\frac{1}{2}})$ . 这与 Example 1 的结果一致.
当 $z = \frac{1}{2}$ 时， $σ_{\frac{1}{2}} (n) \in O (n^{\frac{3}{4}})$ ，即 $\sum_{d ∣ n} \sqrt{d} \in O (n^{\frac{3}{4}})$ . 洛谷 P4980 Polya 定理模板题^[9]的一种比较 trivial 的解法^[10]的时间复杂度证明就来源于此. 我们之后还会在整除分块与杜教筛中见到它.

另外，如果只使用 Proposition 1 ， $- 1 < z < 1$ 部分的渐进上界将只能估计至 $O (n)$ . 因此 Proposition 2 是更为优越的.

约数函数更复杂的上限与渐进估计可参考 Wikipedia^[7].

2 整除分块

也被称为数论分块. 求 $\sum_{i = 1}^{n} f (i) g (⌊ \frac{n}{i} ⌋)$ 我们按 $d = ⌊ \frac{n}{i} ⌋$ 分块求和： $\sum_{d} g (d) \sum_{⌊ \frac{n}{i} ⌋ = d} f (i)$ 可以证明，对一指定的 $d$ ，满足 $d = ⌊ \frac{n}{i} ⌋$ 的 $i$ 取遍一连续区间，故若 $f$ 的前缀和能 $O (1)$ 求出，块数量 $# {⌊ \frac{n}{i} ⌋}_{i = 1}^{n}$ 即该算法的时间复杂度. 注意到当 $i \leq \sqrt{n}$ 时， $⌊ \frac{n}{i} ⌋$ 最多只有 $⌊ \sqrt{n} ⌋$ 种取值，而 $i \geq \sqrt{n}$ 时， $1 \leq ⌊ \frac{n}{i} ⌋ \leq \sqrt{n}$ 表明其也最多只有 $⌊ \sqrt{n} ⌋$ 种取值. 因此整除分块的时间复杂度 $T_{1} (n) = # {⌊ \frac{n}{i} ⌋}_{i = 1}^{n} \leq 2 \sqrt{n} \in O (\sqrt{n})$

方便起见，后文记 $D (n) = {⌊ \frac{n}{i} ⌋}_{i = 1}^{n}$ .

2.1 整除分块嵌套

将 Proposition 2 加强，我们有如下通用放缩：

Proposition 3 $\sum_{d ∣ n} f (d) \leq \sum_{d \in D (n)} f (d) \leq \sum_{i = 1}^{\sqrt{n}} f (i) + f (⌊ \frac{n}{i} ⌋)$

LHS 成立的关键在于 ${d : d ∣ n} \subset D (n)$ ；而 RHS 的本质就是上述对整除分块块数量上界的估计.

注意到 Proposition 2 是 Example 5 证明的核心，而 Proposition 3 是 Proposition 2 的加强版，故仿造 Example 5 的证明，我们有

Example 6 令 $S_{z} (n) = \sum_{d \in D (n)} d^{z}$ 则前述 Example 5 中 $σ_{z} (n)$ 的上界与渐进上界也同样适用于 $S_{z} (n)$ .

现在可以对嵌套整除分块 $\sum_{i = 1}^{n} f (i) \sum_{j = 1}^{⌊ \frac{n}{i} ⌋} g (j) h (⌊ \frac{n}{i j} ⌋)$ 的时间复杂度 $T_{2}$ 做出估计了. 对 Example 6 取 $z = \frac{1}{2}$ ，立刻有 $T_{2} (n) = \sum_{d \in D (n)} T_{1} (d) \leq 2 \sum_{d \in D (n)} \sqrt{d} = 2 S_{\frac{1}{2}} (n) \leq 4 \sqrt{n} P_{\frac{1}{2}} (\sqrt{n}) \in O (n^{\frac{3}{4}})$

我们还可以进一步归纳. 假定 $\forall m \geq 0, \exists z_{m} : 0 \leq z_{m} < 1, T_{m} (n) = O (n^{z_{m}})$ ，我们有

$T_{m + 1} (n) = \sum_{d \in D (n)} T_{m} (d) \leq C \sum_{d \in D (n)} n^{z_{m}} = C S_{z_{m}} (n) \in O (n^{\frac{1 + z_{m}}{2}})$

因此 $z_{m + 1} = \frac{1 + z_{m}}{2}$ . 边界条件 $z_{0} = 0$ ，数列递推求得 $z_{m} = 1 - 2^{- m}$ ，检验满足条件. 因此 $m$ 重嵌套整除分块的时间复杂度 $T_{m} (n) \in O (n^{1 - 2^{- m}})$

3 杜教筛

杜教筛可以以低于线性的时间复杂度求解某些数论函数的前缀和. 其思路并不复杂. 设 $f$ 为一数论函数，我们希望快速求得其前缀和 $\hat{f} (n) = \sum_{i = 1}^{n} f (i)$ . 考虑数论函数 $g$ 和 $h = g * f$ ， $h (n) = \sum_{d ∣ n} g (d) f (\frac{n}{d})$ 两端做前缀和得 $\begin{aligned} \hat{h} (n) & = \sum_{i = 1}^{n} h (i) \\ = \sum_{i = 1}^{n} \sum_{d ∣ i} g (d) f (\frac{i}{d}) \\ = \sum_{d = 1}^{n} g (d) \sum_{i = 1}^{⌊ \frac{n}{d} ⌋} f (i) \\ = \sum_{d = 1}^{n} g (d) \hat{f} (⌊ \frac{n}{d} ⌋) \\ = g (1) \hat{f} (n) + \sum_{d = 2}^{n} g (d) \hat{f} (⌊ \frac{n}{d} ⌋) \end{aligned}$ 因此 $\hat{f} (n) = \frac{1}{g (1)} (\hat{h} (n) - \sum_{d = 2}^{n} g (d) \hat{f} (⌊ \frac{n}{d} ⌋))$

故若 $g$ 、 $h$ 的前缀和可 $O (1)$ 算得，根据上式整除分块即可递归地计算出 $f$ 的前缀和.

下面分析算法的复杂度. 注意到 $⌊ \frac{⌊ \frac{n}{i} ⌋}{j} ⌋ = ⌊ \frac{n}{i j} ⌋$ 故单轮递归涉及到的自变量均可表示为 $d = ⌊ \frac{n}{i} ⌋$ 的形式. 一个 $\hat{f} (d)$ 做整除分块耗时 $T_{1} (d)$ ，若采用记忆化递归，由上节分析，算法总时间复杂度为 $\sum_{d \in D (n)} T_{1} (d) = T_{2} (n) \in O (n^{\frac{3}{4}})$

但我们还可以做得更好——考虑先用 $O (K)$ 的时间复杂度线性筛出前 $K$ 个 $f (n)$ 并求前缀和，则递归求解时， $d \leq K$ 的 $\hat{f} (d)$ 就无需再向下递归了. 为分析此类时间复杂度，对 Proposition 3 做最后一点扩展：

Proposition 4 $\sum_{\begin{matrix} d ∣ n \\ d > K \end{matrix}} f (d) \leq \sum_{\begin{matrix} d \in D (n) \\ d > K \end{matrix}} f (d) \leq \sum_{K < i \leq \sqrt{n}} f (i) + \sum_{1 \leq i \leq min {⌊ \frac{n}{K} ⌋, \sqrt{n}}} f (⌊ \frac{n}{i} ⌋)$

特别的，当 $K > \sqrt{n}$ 时，有

$\sum_{\begin{matrix} d ∣ n \\ d > K \end{matrix}} f (d) \leq \sum_{\begin{matrix} d \in D (n) \\ d > K \end{matrix}} f (d) \leq \sum_{1 \leq i \leq ⌊ \frac{n}{K} ⌋} f (⌊ \frac{n}{i} ⌋)$

故用 Proposition 4 ，当 $K > \sqrt{n}$ 时，算法在递归部分的时间复杂度降低为

$\begin{aligned} {Du}_{K} (n) & = \sum_{\begin{array}{c} d \in D (n) \\ d > K \end{array}} T_{1} (d) \\ = \sum_{1 \leq i \leq ⌊ \frac{n}{K} ⌋} T_{1} (⌊ \frac{n}{i} ⌋) \\ \leq \sum_{1 \leq i \leq ⌊ \frac{n}{K} ⌋} C \sqrt{\frac{n}{i}} \\ = C \sqrt{n} \sum_{1 \leq i \leq ⌊ \frac{n}{K} ⌋} i^{- \frac{1}{2}} \\ = C \sqrt{n} P_{\frac{1}{2}} (⌊ \frac{n}{K} ⌋) \\ \in \sqrt{n} O ({(\frac{n}{K})}^{\frac{1}{2}}) \\ \subset O (n K^{- \frac{1}{2}}) \end{aligned}$

总时间复杂度 $O (K) + O (n K^{- \frac{1}{2}})$

为最小化时间复杂度，取 $K = n^{\frac{2}{3}}$ ，得到最优时间复杂度 $O (n^{\frac{2}{3}})$ .

这部分的时间复杂度证明主要参考了文章^[11].

4 Challenge

Example 7 对 $1$ 到 $n$ 间的无平方因子数计数. $n \leq 10^{18}$ .

参见蓝桥杯 2023 省赛 A 组 J 题《翻转硬币》^[12]或《完全平方数》^[13].

我们指出，无平方因子数有如下计数公式 $f (n) = \sum_{i = 1}^{n} μ^{2} (i) = \sum_{i = 1}^{⌊ \sqrt{n} ⌋} μ (i) ⌊ \frac{n}{i^{2}} ⌋$

朴素实现复杂度为 $O (\sqrt{n})$ ，考虑对 $⌊ \frac{n}{i^{2}} ⌋$ 开发一种新的整除分块算法. 现在问题有三. 一是估计 $# D_{2} (n) = # {⌊ \frac{n}{i^{2}} ⌋}_{i = 1}^{\sqrt{n}}$ 这并不困难，按 $i \leq n^{\frac{1}{3}}$ 和 $i \geq n^{\frac{1}{3}}$ 讨论即知其上界为 $O (n^{\frac{1}{3}})$ .

二是实现方案. 这里也直接给出：

ll sqrtN=sqrt(N);
ll ans=0;
for(ll l=1,r,d;l<=sqrtN;l=r+1){
    d=N/(l*l),r=sqrt(N/d);
    ans+=(S_mu(r)-S_mu(l-1))*d;
}

最后是算法时间复杂度分析. 普通的 $⌊ \frac{n}{i} ⌋$ 整除分块不会因杜教筛增加时间复杂度，但 $⌊ \frac{n}{i^{2}} ⌋$ 则需要额外的讨论. 注意到该整除分块枚举中，需做杜教筛的数的集合为 ${⌊ {(⌊ \frac{n}{d} ⌋)}^{\frac{1}{2}} ⌋}_{d \in D_{2} (n)}$ 同样类似 Proposition 3 ，我们有

Proposition 5 $\sum_{d^{2} ∣ n} f (\frac{n}{d^{2}}) \leq \sum_{d \in D_{2} (n)} f (d) \leq \sum_{i = 1}^{n^{\frac{1}{3}}} f (i) + f (⌊ \frac{n}{i^{2}} ⌋)$

因此算法递归部分时间复杂度可估计为 $\begin{aligned} \sum_{d \in D_{2} (n)} {Du}_{K} (⌊ {(⌊ \frac{n}{d} ⌋)}^{\frac{1}{2}} ⌋) & \leq \sum_{d \in D_{2} (n)} C ⌊ {(⌊ \frac{n}{d} ⌋)}^{\frac{1}{2}} ⌋ K^{- \frac{1}{2}} \\ \leq C K^{- \frac{1}{2}} (\sum_{i = 1}^{n^{\frac{1}{3}}} {(\frac{n}{\frac{n}{i^{2}}})}^{\frac{1}{2}} + \sum_{i = 1}^{n^{\frac{1}{3}}} {(\frac{n}{i})}^{\frac{1}{2}}) \\ = C K^{- \frac{1}{2}} (\sum_{i = 1}^{n^{\frac{1}{3}}} i + n^{\frac{1}{2}} \sum_{i = 1}^{n^{\frac{1}{3}}} i^{- \frac{1}{2}}) \\ \in K^{- \frac{1}{2}} (O (n^{\frac{2}{3}}) + n^{\frac{1}{2}} O (n^{\frac{1}{6}})) \\ \subset O (n^{\frac{2}{3}} K^{- \frac{1}{2}}) \end{aligned}$ 总时间复杂度为 $O (K) + O (n^{\frac{2}{3}} K^{- \frac{1}{2}})$ 取 $K = n^{\frac{4}{9}}$ ，得到最优时间复杂度 $O (n^{\frac{4}{9}})$ . 代入 $n = 10^{18}$ ，量级约为 $10^{8}$ .

这估计并不算优秀. 传言存在 $O (n^{\frac{2}{5}})$ 的估计，猜测大概优化了 ${⌊ \frac{n}{i} ⌋}_{i = 1}^{n}$ 和 ${⌊ {(⌊ \frac{n}{d} ⌋)}^{\frac{1}{2}} ⌋}_{d \in D_{2} (n)}$ 的重叠部分。笔者尚未找出其推导方式.文章来源地址https://www.toymoban.com/news/detail-417815.html

References

1. Abuse of notation - wikipedia. (n.d.). https://en.wikipedia.org/wiki/Abuse_of_notation#Function_notation.

2. Graham, R. L., Knuth, D. E., & Patashnik, O. (1994). Concrete mathematics: A foundation for computer science (second, pp. 443–449). Addison-Wesley.

3. Big o notation - wikipedia # family of bachmann–landau notations. (n.d.). https://en.wikipedia.org/wiki/Big_O_notation#Family_of_Bachmann%E2%80%93Landau_notations.

4. 复杂度 - OI wiki. (n.d.). https://oi-wiki.org/basic/complexity/#%E6%B8%90%E8%BF%9B%E7%AC%A6%E5%8F%B7%E7%9A%84%E5%AE%9A%E4%B9%89.

5. Knuth, D. E. (1976). Big omicron and big omega and big theta. SIGACT News, 8(2), 18–24. https://doi.org/10.1145/1008328.1008329

6. Graham, R. L., Knuth, D. E., & Patashnik, O. (1994). Concrete mathematics: A foundation for computer science (second, pp. 47–56). Addison-Wesley.

7. Divisor function - wikipedia # growth_rate. (n.d.). https://en.wikipedia.org/wiki/Divisor_function#Growth_rate.

8. sun123zxy. (2020). sun123zxy’s blog - 原创OI题目 GCD卷积 problem and solution. https://blog.sun123zxy.top/posts/20201206-gcdconv/.

9. P4980 【模板】pólya 定理 - 洛谷 | 计算机科学教育新生态. (n.d.). https://www.luogu.com.cn/problem/P4980.

10. sun123zxy. (2020). sun123zxy’s blog - 等价类计数：Burnside引理 & Polya定理. http://blog.sun123zxy.top/posts/20200321-burnside/#s-4.3.

11. Ander. (2022). 杜教筛. https://zhuanlan.zhihu.com/p/521699400.

12. P9238 [蓝桥杯 2023 省 a] 翻转硬币 - 洛谷 | 计算机科学教育新生态. (n.d.). https://www.luogu.com.cn/problem/P9238.

13. P4318 完全平方数 - 洛谷 | 计算机科学教育新生态. (n.d.). https://www.luogu.com.cn/problem/P4318.

到了这里，关于OI 数论中的上界估计与时间复杂度证明的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！