通过这篇博客,你将清晰的明白什么是如何区别欠拟合与过拟合。这个专栏名为白话机器学习中数学学习笔记,主要是用来分享一下我在 机器学习中的学习笔记及一些感悟,也希望对你的学习有帮助哦!感兴趣的小伙伴欢迎私信或者评论区留言!这一篇就更新一下《 白话机器学习中的数学——学习曲线:如何区别欠拟合与过拟合》
一、过拟合
前面我们聊了很多过拟合的话题,即模型学习了很多训练集特有的属性。导致模型对于训练集有很好的拟合效果,而对于未知数据的预测能力很差,模型的泛化能力很差。而反过来又有一种叫作欠拟合的状态,用英文说是 underfitting。在这种情况下模型的性能也会变差。
一个是过度训练,一个是过度不训练。所以我们追求的是恰好训练,这个度是很难把握的,需要我们不断实验去挑战参数,最终达成最优效果。
欠拟合是与过拟合相反的状态,所以它是没有拟合训练数据的状态。用直线对图中这种拥有复杂边界线的数据进行分类的情况,无论怎样做都不能很好地分类,最终的精度会很差。
出现这种情况的主要原因就是模型相对于要解决的问题来说太简单了,原因也和过拟合的情况相反。过拟合与欠拟合基本上是相反关系,原因不同,解决方案也不同。解决欠拟合的方法有很多,比如增加数据量,增加训练次数等。
二、区分过拟合与欠拟合
但是,我们只对模型进行评估,然后根据得到的模型精度就能判断模型是过拟合还是欠拟合吗?显然,只根据精度不能判断是哪种不好的拟合。那怎么样才能判断到底是过拟合还是欠拟合呢?
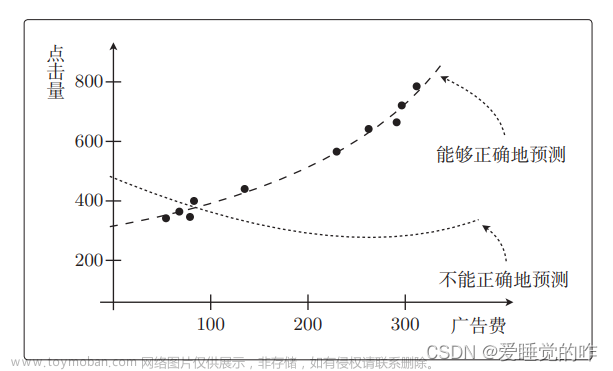
我们以数据的数量为横轴、以精度为纵轴,然后把用于训练的数据和用于测试的数据画成图来看一看就知道了。我们具体来看一个例子吧。考虑一下使用这样的 10 个训练数据进行回归的场景:
这些数据似乎用二次函数来拟合比较合适。不过这里我们先假设 fθ(x)是一次函数。接着,只随便选择
其中的 2 个数据用作训练数据。那 fθ(x)就是这样的:
在这个状态下,2 个点都完美拟合,误差为 0。那这次把 10 个数据都用来训练呢?
不过在这种情况下,误差已经无法为 0 了。这里我想说的就是如果模型过于简单,那么随着数据量的
增加,误差也会一点点变大。换句话说就是精度会一点点下降。把这种情况画在刚才所说的以数据的数量为横轴、以精度为纵轴的图上,形状大体上就是这样的:
一开始精度很高,但随着数据量的增加,精度一点点地变低了。接下来用测试数据来评估一下。假设在刚才的 10 个训练数据之外,还有测试数据。我们用这些测试数据来评估各个模型,之后用同样的方法求出精度,并画成图。训练数据较少时训练好的模型难以预测未知的数据,所以精度很低;反过来说,训练数据变多时,预测精度就会一点点地变高。用图来展示就是这样的:
三、高偏差和高方差
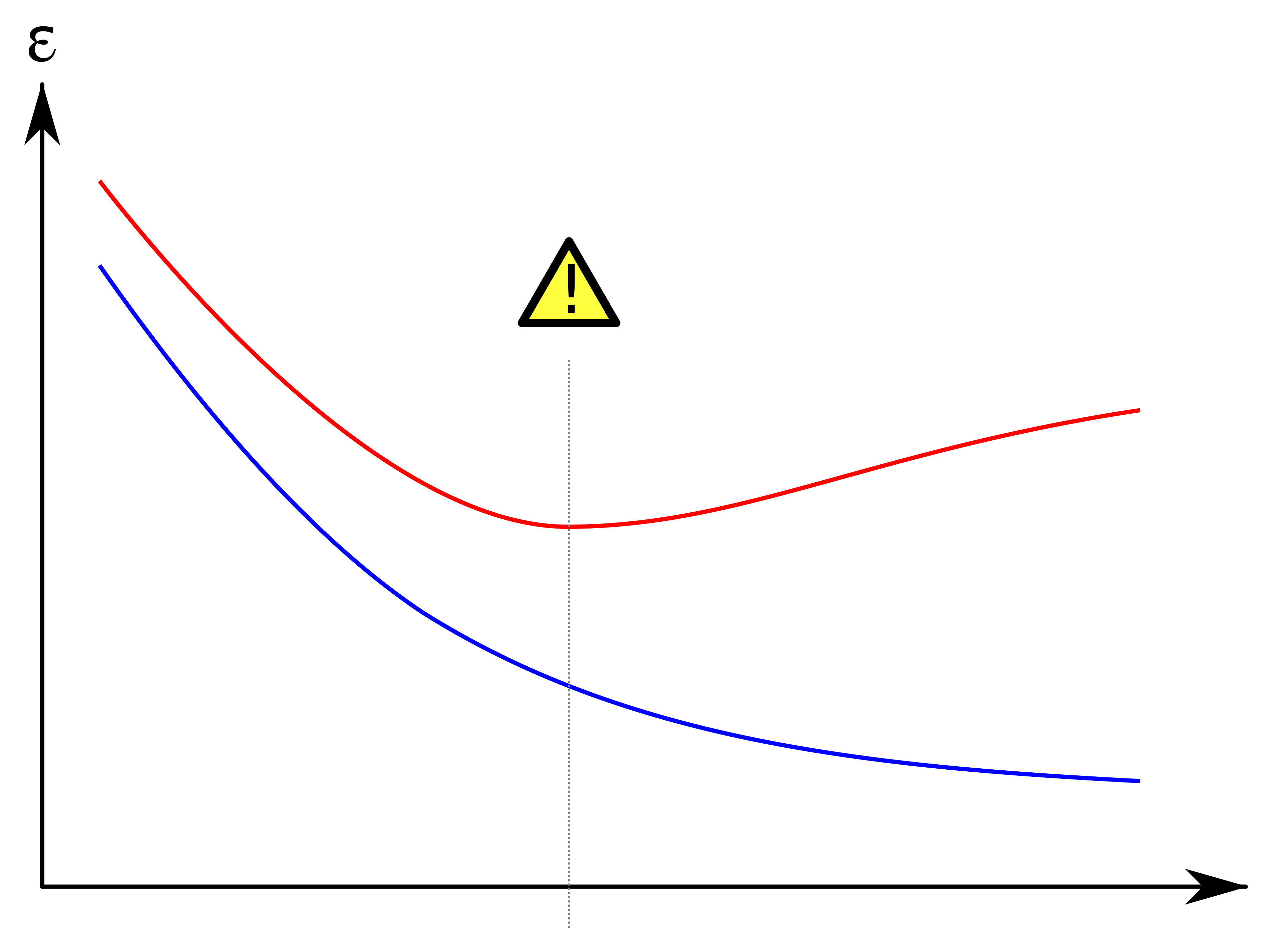
将两份数据的精度用图来展示后,如果是这种形状,就说明出现了欠拟合的状态。也有一种说法叫作高偏差,指的是一回事。这是一种即使增加数据的数量,无论是使用训练数据还是测试数据,精度也都会很差的状态。
而在过拟合的情况下,图是这样的。这也叫作高方差:
随着数据量的增加,使用训练数据时的精度一直很高,而使用测试数据时的精度一直没有上升到它的水准。也就是说,只对训练数据拟合得较好,这就是过拟合的特征。这张图中需要注意的点在这里:
这两张图分别展示了欠拟合和过拟合的特征。文章来源:https://www.toymoban.com/news/detail-418368.html
四、总结
像这样展示了数据数量和精度的图称为学习曲线。在知道模型精度低,却不知道是过拟合还是欠拟合的时候,画一下学习曲线就好了。通过学习曲线判断出是过拟合还是欠拟合之后,就可以采取相应的对策以便改进模型了。模型评估听上去很简单,但其实有很多内容。关于模型评估的指标和方法,除了今天讲的之外还有其他的,有兴趣的话大家自己研究一下哦。文章来源地址https://www.toymoban.com/news/detail-418368.html
到了这里,关于机器学习中的数学——学习曲线如何区别欠拟合与过拟合的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!