基本运算放大电路-Toy模板网

这篇具有很好参考价值的文章主要介绍了基本运算放大电路。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

我先说明。下面的内容应该很多人都看到过，但是我建议还是细看，最好自己推一下。我就是这么做的。

运算放大器工作原理综述：
　　运算放大器组成的电路五花八门，令人眼花瞭乱，在分析运算放大器工作原理时倘没有抓住核心，往往令人头大。本文收集运放电路的应用电路，希望看完后有所收获。但是在分析各个电路之前，还是先回忆一下两个运放教材里必教的技能，就是“虚短”和“虚断”。

“虚短”是指在分析运算放大器处于线性状态时，可把两输入端视为等电位，这一特性称为虚假短路，简称虚短。显然不能将两输入端真正短路。

“虚断”是指在分析运放处于线性状态时，可以把两输入端视为等效开路，这一特性称为虚假开路，简称虚断。显然不能将两输入端真正断路。
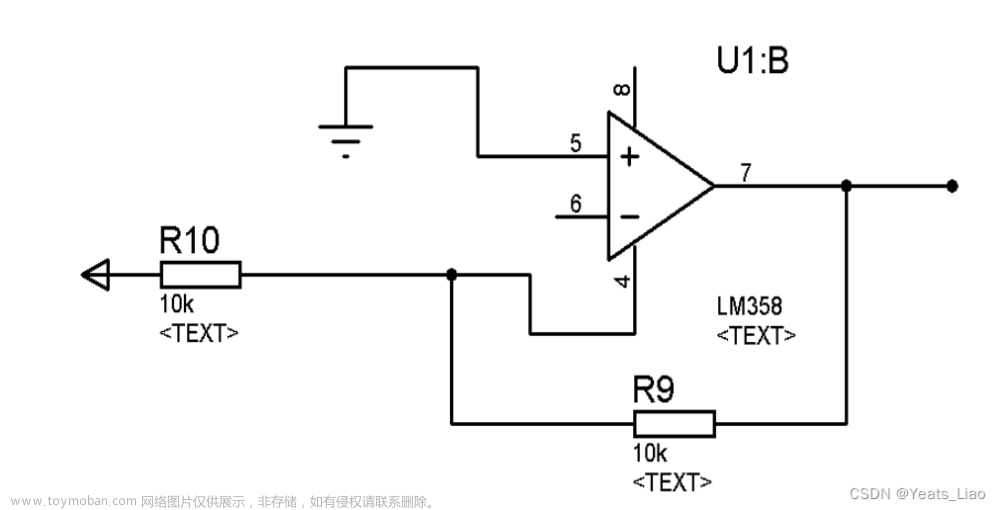
1.反向放大器
　　图一运算放大器的同向端接地=0V，反向端和同向端虚短，所以也是0V。
反向输入端输入电阻很高，虚断（可以看作是断路），反向输入端几乎没有电流注入和流出（虚断），那么R1和R2相当于是串联的，流过一个串联电路中的每一只组件的电流是相同的，即流过R1的电流和流过R2的电流是相同的。
流过R1的电流I1 = (Vi - V-)/R1
流过R2的电流I2 = (V- - Vout)/R2
V- = V+ = 0由虚短可知，同相输入端接地导致反响输入端电位也是0v。
I1 = I2 由于虚断，等效位串联，那么流过R1和R2的电流是一个电流。
求解上面的初中代数方程得：
Vout = (-R2/R1)Vi 注意看有个负号
这就是传说中的反向放大器的输入输出关系式了。

2.同相放大器
图中Vi与V-虚短，则 Vi = V-
因为虚断，反向输入端没有电流输入输出（相当于断路），通过R1和R2 的电流相等，设此电流为I，由欧姆定律得： I = Vout/(R1+R2)
Vi等于R2上的分压（虚断结合虚短可得），即：Vi = IR2
由上面的式子得到Vout=Vi(R1+R2)/R2 这就是传说中的同向放大器的公式了。（注意没有负号）
基本运算放大电路
3.反相加法器
图三中，由虚短知： V- = V+ = 0由虚断及基尔霍夫定律知，通过R2与R1的电流之和等于通过R3的电流，故 (V1 – V-)/R1 + (V2 – V-)/R2 = ( V- Vout)/R3 (R3电流假如从左到右)
又因为V-=V+=0v,所以V1/R1 + V2/R2 = -Vout/R3 如果取R1=R2=R3，则上式变为Vout=-（V1+V2）注意负号，这就是反向加法器了。
这里我说明一下( V- Vout)/R3 ，我们电流参考方向假如是下图的方向，显然我们人为规定电流的流向是从高电位到低电位（电流就像水，电压就像山，水自然是从高到低的流）。由于虚短V-的电位是0v，而电流是从V-流向Vout，那么意味着Vout的电位是低于V-的，那么Vout是一个负的电位。那么V-与Vout的电压就是V- 减去Vout。那么算出来的Vout正好就是负值。然后再除R3得到电流。
基本运算放大电路
4.同相加法器
看下图。因为虚断，运算放大器同向端没有电流流过，则流过R1和R2的电流相等。（R1和R2组成的串联电路，如果两端也有压差，自然就有电流）
同理流过R4和R3的电流也相等。（R3和R4的压差就是Vout）
故 (V1 – V+)/R1 = (V+ - V2)/R2 （这里我们给一个电流的参考方向顺时针）
同理(Vout – V-)/R3 = V-/R4
由虚短知： V+ = V-
如果R1=R2，R3=R4，
则由以上式子可以推导出
V+ = (V1 + V2)/2 V- = Vout/2 故 Vout = V1 + V2 是一个加法器。

基本运算放大电路
5减法器
图五由虚断知，通过R1的电流等于通过R2的电流。
，同理通过R4的电流等于R3的电流，
故有 (V2 – V+)/R1 = V+/R2 （假如电流是顺时针）
(V1 – V-)/R4 = (V- - Vout)/R3 （假如电流是顺时针）
如果R1=R2，则V+ = V2/2
如果R3=R4，则V- = (Vout + V1)/2
由虚短知 V+ = V-
所以 Vout=V2-V1 这就是传说中的减法器了。
基本运算放大电路
这里再补充一个分析减法运放的方法：主要应用了叠加原理

看上图
分析减法运算电路用叠加原理比较简单。分别将输入信号ui1和ui2单独作用时的电路。

显然Ui1单独作用的时候，是一个反向比例运放
U0=-（Rf/R1）xUi1 公式1
基本运算放大电路
那么Ui2单独作用的时候
上图是一个同相比例放大电路
Ui2经过R3分压，就是Up=Ui2xR3/(R2+R3) 这里的Up指的是同相的输入电压
在带入同相比例运放的公式当中
同相比例运放的公式：V0=Vix(R1+Rf)/R1
我们的Vi=Up
V0=Ui2xR3/(R2+R3)X（R1+Rf）/R1 公式2
然后我们将公式2和公式1相加就能得到最终的输出
V0=Ui2xR3/(R2+R3)X（R1+Rf）/R1-（Rf/R1）xUi1
这里就得分三种分析
一种R1=Rf R2=R3
V0=Vi2-Vi
另一种R1=R3 R2= Rf 原文并没有这个，我只是自己试了一下
这一步我写清楚一点
V0=Ui2xR3/(R2+R3)x(R1+Rf)/R1-Rf/R1xUi1=Ui2xR3/(R2+R3)x(R3+R2)/R3-R2/R3xUi1=-R2/R3xUi1+Ui2
有兴趣的推一下
第三种
R1=R2 R3=Rf
这种的过程如下
V0=-R3/R1xUi1+R3/(R1+R3)xUi2+R3/R1xR3/(R1+R3)xUi2=R3/(R1+R3)xUi2x(1+R3/R1)-R3/R1xui1 这里补充一句1+R3/R1=（R1+R3）/R1 而这个刚好跟R3/(R1+R3)的分母抵消掉，所以最终V0=R3/R1xUi2-R3/R1xUi1=-R3/R1x(Ui1-Ui2)
完美！！！建议自己推一下

6积分
　　图六电路中，由运算放大器的虚短知，反向输入端的电压与同向端相等，是0V
由虚断知，通过R1的电流与通过C1的电流相等。
通过R1的电流 i=V1/R1
通过C1的电流i=C*（dUc/dt）=-C*（dVout/dt ）（同样我们认为电流是顺时针）
想想看，反向端因为虚短是0v，那么电流是从反向端V-流向，再从C1流向Vout。显然Vout是一个负电压。所以上式字中才出现负号。
这里补充一下，I=dq/dt 电流是单位时间里，流过的电荷。
而Q=CU 想一下，电容C两端的电压，实际上就是电容两端存有的异种电荷数量的多少。那么电荷数是Q，电容式C，电压是U。
i=(dq/dt)=Cdu/dt 注意电容容值是常量
那么连立上面的式子就知道 idt=-cdVo 这里为了避免混淆，此处用Vo代替Vout
因为上面推导的结论i=V1/R1
这里我们用S代表积分号， SV1/Rdt=-SCdVo
上式中1/R是常量可以提到积分号外边，那么左侧就是1/R乘电压V1对时间t的积分再
等式右边是-C是常量提到积分号外边，再乘Vo对自己的积分CVo(这里得说一下，常数1对一个变量的积分等于该积分变量本身)。那就是-CVo
综上：-CVo=1/R1SV1dt 简化就是SV1dt=-(R1C)Vout
所以输出电压与输入电压对时间的积分成正比,这就是传说中的积分电路了
显然如果V1是个常量的话，上式就是Vo=-V1/(CR1)t。则Vout输出电压是一条从0至负电源电压按时间变化的直线。

7.微分
　　图七中由虚断知，通过电容C1和电阻R2的电流是相等的，由虚短知，运算放大器同向端与反向端电压是相等的。则： Vout = -i * R2 = -(R2C1)dV1/dt 这是一个微分电路。如果V1是一个突然加入的直流电压，则输出Vout对应一个方向与V1相反的脉冲。
　　
8.差分

首先从虚短知道
Vx=V1 Vy=V2
由虚断可以知道放大器的反向输入端没有电流流过，看作断路
让么R1, R2, R3看作是串联。
那么流过这三个电阻的电流也就是相等的
所以，I=(Vx-Vy)/R2 公式1
Vo1-Vo2=I(R1+R2+R3) =
(Vx-Vy)(R1+R2+R3)/R2 公式2
由于虚断那么流过R6和R7的电流是一样的
假设R6=R7
那么Vo2/2=Vw 公式3
同理假如R4=R5
那么Vout-Vu=Vu-Vo1
所以Vu=(Vout+Vo1)2 公式4
由于虚短Vu=Vw 公式5
结合公式345
Vu=Vw=Vo2/2=(Vout+Vo1)/2
所以Vout=Vo2-Vo1 公式6
再结合公式26
Vout=Vo2-Vo1=Vo1-Vo2=-(Vx-Vy)(R1+R2+R3)/R2 (注意负号)
最终得到：Vout=-(Vx-Vy)*(R1+R2+R3)/R2 （注意负号）
这个电路就是传说中的差分放大电路了。

9.应用
基本运算放大电路
分析一个大家接触得较多的电路。
很多控制器接受来自各种检测仪表的0到20mA或4到20mA电流，电路将此电流转换成电压后再送ADC转换成数字信号
图九就是这样一个典型电路。
如图4到20mA电流流过采样100Ω电阻R1，在R1上会产生0.4V到2V的电压差。
由虚断知，运算放大器输入端没有电流流过，则流过R3和R5的电流相等，流过R2和R4的电流相等。
所以 (V2-Vy)/R3 = Vy/R5 公式1
(V1-Vx)/R2 = (Vx-Vout)/R4 公式2
由虚短知： Vx = Vy 公式3
电流从0到20ma变化
则V1 = V2 + (0.4到2V) 公式4
由公式34代入2式得
(V2 + (0.4V到2V)-Vy)/R2 = (Vy-Vout)/R4 公式5
如果R3=R2，R4=R5
则由公式5减去公式1得
Vout = -(0.4~2)R4/R2 公式6
图九中R4/R2=22k/10k=2.2
则公式6 Vout = -(0.88到4.4)V
即是说，将420mA电流转换成了-0.88 ~ -4.4V电压，此电压可以送ADC去处理。

10.应用（由于能理有限，暂不清楚RL对电路的影响）
基本运算放大电路

电流可以转换成电压，电压也可以转换成电流。图十就是这样一个电路。上图的负反馈没有通过电阻直接反馈，而是串联了三极管Q1的发射结，大家可不要以为是一个比较器就是了。只要是放大电路，虚短虚断的规律仍然是符合的!
由虚断知，运算放大器输入端没有电流流过，

则 (Vi – V1)/R2 = (V1 – V4)/R6 ……a

同理 (V3 – V2)/R5 = V2/R4 ……b

由虚短知 V1 = V2 ……c

如果R2=R6，R4=R5，则由abc式得V3-V4=Vi

上式说明R7两端的电压和输入电压Vi相等，则通过R7的电流I=Vi/R7，如果负载RL<<100KΩ，则通过Rl和通过R7的电流基本相同。

（备注一下，这个电路提到了RL的电阻值与R1流过的电压的关系，这里我不明白，懂的朋友可以在评论区交流一下，谢谢。）

11.反向求和

基本运算放大电路
对于上图，我们先从前一级的运放开始分析
结合前文分析的电路知道，第一个运放是一个反向放大器，前文讲到过。
那么反向放大器的特点是Vo1=(-Rf1/R1)xVs1
那么显然当Rf1=R1的时候Vo1=-Vs1 注意负号
另外我们在接着看剩下的电路
基本运算放大电路
上面的电路就构成了一个反向加法器，前文也讲到过
我们这里直接使用结论
Vo=-(Vs2+V01)
又因为当Rf1=R1的时候Vo1=-Vs1 注意负号
V0=Vs1-Vs2

内容出处：
http://forum.eepw.com.cn/thread/196953/1
http://www.elecfans.com/dianzichangshi/20170515516147.html
图片来自网络文章来源地址https://www.toymoban.com/news/detail-418737.html

到了这里，关于基本运算放大电路的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！