【机器学习实战】K- 近邻算法（KNN算法）-Toy模板网

这篇具有很好参考价值的文章主要介绍了【机器学习实战】K- 近邻算法（KNN算法）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

K-近邻算法

一、概述

K-近邻算法，又称为 KNN 算法，是数据挖掘技术中原理最简单的算法。

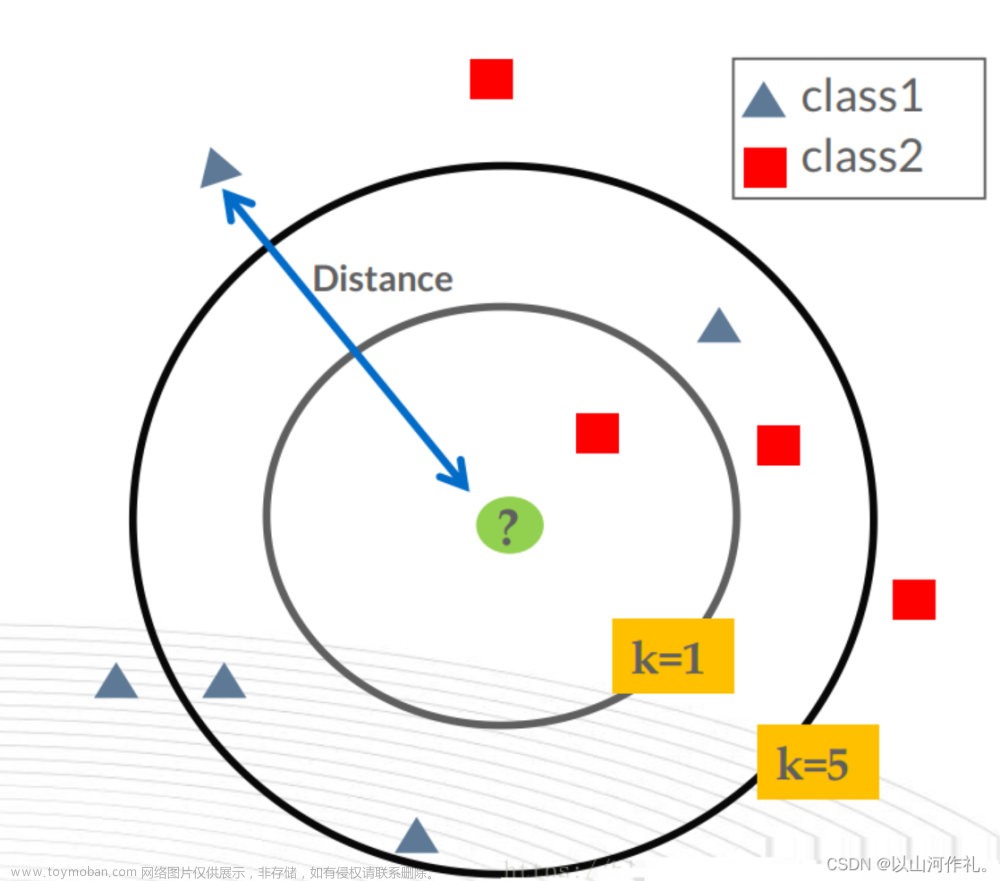
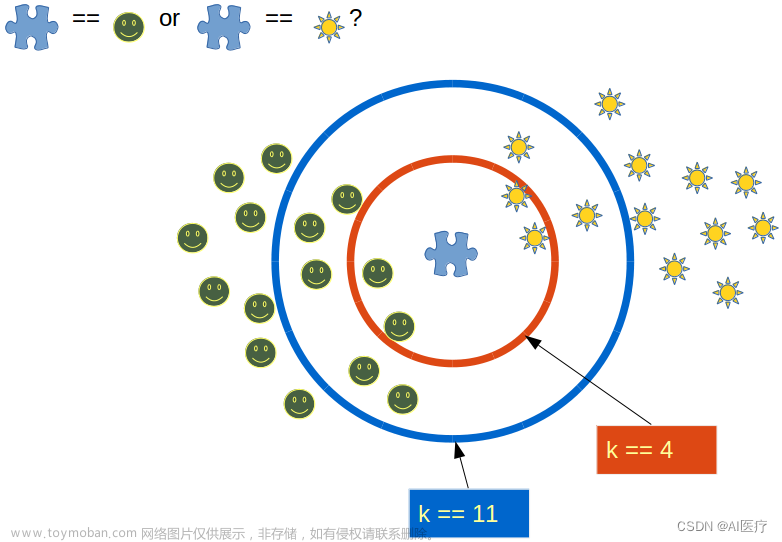
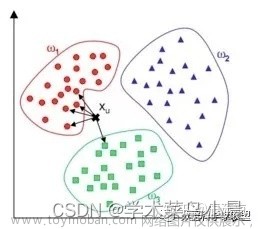
KNN 的工作原理：给定一个已知类别标签的数据训练集，输入没有标签的新数据后，在训练数据集中找到与新数据最临近的 K 个实例。如果这 K 个实例的多数属于某个类别，那么新数据就属于这个类别。

简单理解为：由那些离 X 最近的 K 个点来投票决定 X 归为哪一类

【机器学习实战】K- 近邻算法（KNN算法）

举个例子，可以用 KNN 算法来分类一部电影是爱情片还是动作片（利用打架镜头和接吻镜头来做大致判断）

【机器学习实战】K- 近邻算法（KNN算法）

这个表就是我们已有的数据集合，也就是训练样本集。

这个数据集有两个特征 - 打斗镜头数和亲吻镜头数。
除此之外，我们还知道每部电影的所属类型，即分类样本。

那么这样子我们该如何运用KNN算法来判断表中的新电影所属的电影类别呢？如下图所示

【机器学习实战】K- 近邻算法（KNN算法）从散点图中我们可以分析大致推断，这个电影很有可能是爱情片，因为它的距离和已知的三个爱情片更近一点。

KNN 算法是利用什么方法进行判断的呢？
没错，就是距离度量 ✨

在二维平面中可以使用高中就学过的距离计算公式 $【机器学习实战】K- 近邻算法（KNN算法）$

如果是多个特征拓展到 N维空间 的话，我们可以使用欧氏距离（也称欧几里得度量），如下所示：

$【机器学习实战】K- 近邻算法（KNN算法）$

通过计算可以得到训练集中所有的电影和新电影之间的距离，如下图所示

【机器学习实战】K- 近邻算法（KNN算法）

通过表中的计算结果，我们可以知道绿点标记的电影到爱情片《后来的我们》距离最近，为 29.1.但如果只靠这样来判断的话，这个算法应该叫最近邻算法。

KNN算法的步骤如下（一般 k ≤ 20）

计算已知类别数据集中的点与当前点之间的距离
按照距离递增次序排序
选取与当前距离最小的k个点
确定前k个点所在类别的出现频率
返回前k个点出现频率最高的类别作为当前点的预测类别

通过统计，当 k = 4 的时候，这四部电影的类别统计为 爱情片：动作片 = 3 ： 1 ，出现频率最高的类别是爱情片，所以在 k = 4 的时候，新电影的类别为爱情片

KNN的python实现

1.1构建已经分类好的原始数据集

import pandas as pd
rowdata={'电影名称':['无问西东','后来的我们','前任3','红海行动','唐人街探案','战狼2'],
         '打斗镜头':[1,5,12,108,112,115],
         '接吻镜头':[101,89,97,5,9,8],
         '电影类型':['爱情片','爱情片','爱情片','动作片','动作片','动作片']}
movie_data = pd.DataFrame(rowdata)
movie_data

【机器学习实战】K- 近邻算法（KNN算法）

1.2.算已知类别数据集中的点与当前点之间的距离

new_data = [24, 67]
dist = list((((movie_data.iloc[:6, 1: 3] - new_data)**2).sum(1))**0.5)  * 对行求和

1.3将距离升序排列，然后选取距离最小的k个点

k = 4
dist_l = pd.DataFrame({'dist': dist, 'labels': (movie_data.iloc[:6, 3])})
dr = dist_l.sort_values(by = 'dist')[: k]
dr

1.4 确定前k个点所在类别的出现频率

re = dr.loc[:, 'labels'].value_counts()
re.index[0]

result = []
result.append(re.index[0])
result

封装函数

import pandas as pd
"""
函数功能：KNN分类器
参数说明：
    inX：需要预测的数据集
    dataSet:已知分类标签的数据集（训练集）
    k:k-近邻算法参数，选择距离最小的k个点
返回：
result：分类结果
"""
def classify0(inX, dataSet, k):
    result = []
    dist = list((((dataSet.iloc[:6, 1: 3] - inX)**2).sum(1))**0.5)
    dist_l = pd.DataFrame({'dist': dist, 'labels': (dataSet.iloc[:6, 3])})
    dr = dist_l.sort_values(by = 'dist')[: k]
    re = dr.loc[:, 'labels'].value_counts()
    result.append(re.index[0])
    return result

小结

分类器并不会得到百分比正确的结果，除此之外，分类器的性能也会受到很多因素的影响，比如k的取值就会在很大程度上影响了分类器的预测结果，还有分类器的设置、原始数据集等等。
为了测试分类效果，我们将原始数据集分为两部分一部分用来训练算法（称为训练集），一部分用来测试算法的准确率（称为测试集）

k-近邻算法之约会网站配对效果判定

海伦一直使用在线约会网站寻找适合自己的约会对象，尽管约会网站会推荐不同的人选，但她并不是每一个都喜欢，经过一番总结，她发现曾经交往的对象可以分为三类：
1.不喜欢的人
2.魅力一般的人
3.极具魅力得人
海伦收集约会数据已经有了一段时间，她把这些数据存放在文本文件datingTestSet.txt中，其中各字段分别为：

每年飞行常客里程
玩游戏视频所占时间比
每周消费冰淇淋公升数

1.准备数据

datingTest = pd.read_table('datingTestSet.txt',header=None)
datingTest.head()

datingTest.shape

datingTest.info()

2. 分析数据

%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt

# 将不同标签用颜色区分
Colors = []
for i in range(datingTest.shape[0]):
    m = datingTest.iloc[i,-1]
    if m =='didntLike':
        Colors.append('black')
    if m =='smallDoses':
        Colors.append('orange')
    if m =='largeDoses':
        Colors.append('red')

# 绘制两两之间的散点图
plt.rcParams['font.sans-serif']=['Simhei'] #图中字体设置为黑体
pl=plt.figure(figsize=(12,8))
fig1=pl.add_subplot(221)
plt.scatter(datingTest.iloc[:,1],datingTest.iloc[:,2],marker='.',c=Colors)
plt.xlabel('玩游戏视频所占时间比')
plt.ylabel('每周消费冰淇淋公升数')
fig2=pl.add_subplot(222)
plt.scatter(datingTest.iloc[:,0],datingTest.iloc[:,1],marker='.',c=Colors)
plt.xlabel('每年飞行常客里程')
plt.ylabel('玩游戏视频所占时间比')

fig3=pl.add_subplot(223)
plt.scatter(datingTest.iloc[:,0],datingTest.iloc[:,2],marker='.',c=Colors)
plt.xlabel('每年飞行常客里程')
plt.ylabel('每周消费冰淇淋公升数')
plt.show()

【机器学习实战】K- 近邻算法（KNN算法）

3. 数据归一化

【机器学习实战】K- 近邻算法（KNN算法）

我们很容易发现，上面公式中差值最大的属性对计算结果的影响最大，也就是说每年飞行常客里程对计算结果的影响远远大于其他两个特征，原因仅仅是因为它的数值比较大，但是在海伦看来这三个特征是同等重要的，所以接下来我们要进行数值归一化的处理，使得这三个特征的权重相等。
数据归一化的处理方法有很多种，比如0-1标准化、Z-score标准化、Sigmoid压缩法等等

在这里我们使用最简单的0-1标准化，公式如下：

数据处理中0-1规范化和标准化 - 知乎 (01标准化)

def minmax(dataSet):
    minDf = dataSet.min()
    maxDf = dataSet.max()
    normSet = (dataSet - minDf)/(maxDf - minDf)
    return normSet

将我们的数据集带入函数，进行归一化处理

datingT = pd.concat([minmax(datingTest.iloc[:, :3]), datingTest.iloc[:,3]], axis=1)
datingT.head()

4. 划分训练集和测试集

通常来说，我们只提供已有数据的90%作为训练样本来训练模型，其余10%的数据用来测试模型的准确性

"""
函数功能：切分训练集和数据集
参数说明
    dataSet:原始数据集
    rate:训练集所占的比例
返回：切分好的训练集和数据集
"""
def randSplit(dataSet, rate = 0.9):
    n = dataSet.shape[0]
    m = int(n * rate)
    train = dataSet.iloc[:m, :]
    test = dataSet.iloc[m: ,:]
    test.index = range(test.shape[0])
    return train, test

train, test = randSplit(datingT)
train
test

5. 分类器针对于约会网站的测试代码

上面我们已经将原始数据进行归一化处理然后也切分了训练集和测试集，所以我们的函数的输出参数就可以是 train、test、和**k** (选择的距离最小的k个点)

"""
函数功能：KNN 算法分类器
参数说明：
    train:训练集
    test：测试集
    k：KNN参数，即距离最小的k个点
返回：预测好分类的测试集
"""
def datingClass(train, test, k):
    n = train.shape[0] - 1
    m = test.shape[0]
    result = []
    for i in range(m):
        dist = list((((train.iloc[:6, 1: 3] - test.iloc[1, :n])**2).sum(1))**5)
        dist_l = pd.DataFrame({'dist':dist, 'labels':(train.iloc[:, n])})
        dr = dist_l.sort_values(by = 'dist')[: k]
        re = dist.loc[:, 'labels'].value_counts()
        result.append(re.index[0])
    result = pd.Series(result)
    test['predict'] = result
    acc = (test.iloc[:,-1] == test.iloc[:, -2]).mean()
    print(f'模型预测准确率为{acc}')
    return test

最后，测试上述代码能否正常运行，使用上面生成的测试集和训练集导入分类器函数中，然后执行并查看分类结果

datingClass(train, test, 5)

【机器学习实战】K- 近邻算法（KNN算法）

总结文章来源地址https://www.toymoban.com/news/detail-418943.html

k近邻
算法功能	分类（核心），回归
算法类型	有监督学习 - 惰性学习，距离类模型
数据输入	包含数据标签 y，且特征空间中至少包含k 个训练样本 (k ≥ 1)
特征空间中各个特征的量纲需统一，若不统一则需要进行归一化处理
自定义的超参数 k (k ≥ 1)
模型输出	在KNN分类中，输出是标签中的某个类别
在KNN回归中，输出是对象的属性值，该值是距离输入的数据最近的k个训练样本标签的平均值