广度优先搜索算法-Toy模板网

这篇具有很好参考价值的文章主要介绍了广度优先搜索算法。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一点睛

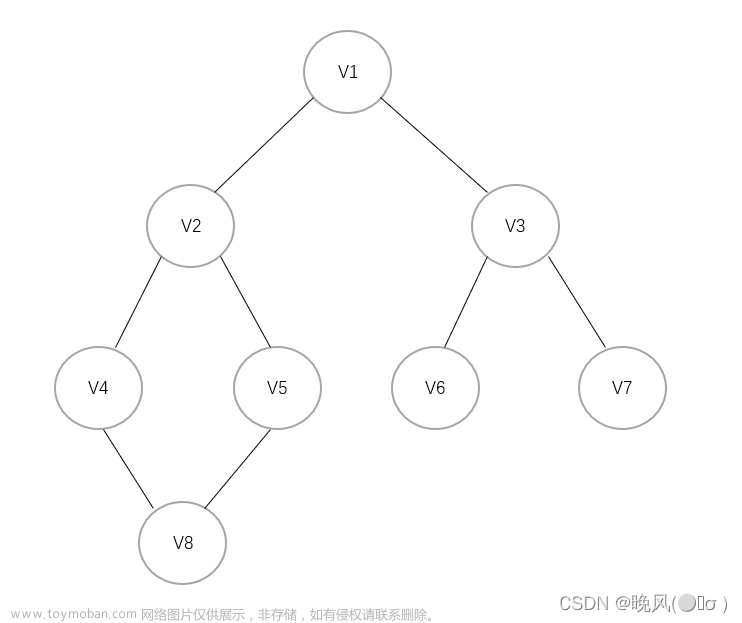
树的广度优先搜索实际上就是层次遍历。首先遍历第 1 层，然后第 2 层......同一层次按照从左到右的顺序访问，直到最后一层。一棵树如下图所示，先遍历第 1 层 A，然后遍历第 2 层的 B 和 C，再遍历第 3 层的 D、E、F，最后遍历第 4 层的 G。

二分支限界法

分支限界法通常以广度优先或最小耗费（最大效益）优先的方式搜索问题的解空间树。活节点表是关键数据结构。活节点表的实现通常有两种形式：一种是普通队列，即先进先出队列，另外一种是优先级队列，按照优先级决定哪个节点为当前扩展节点。根据活节点表不同，分支限界法分为以下两种：队列式分支限界法和优先队列分支限界法。

分支限界法的问题秘籍如下。

1 定义解空间

2 确定解空间的组织结构

3 搜索解空间

三队列式分支限界法解决背包问题算法设计

1 定义问题的解空间

背包问题属于典型的 01 背包问题，问题的解是从 n 个物品张选择一些物品，使其在不超过容量的情况下价值最大。每个物品都有且只有两种状态：要么被装入，要么不被装入。那么第 i 个物品被装入达到目标还是不被装入呢？显然还不确定。因此，可以用变量 Xi 表示第 i 个物品是否被装入背包的状态，用 0 表示不被装入，用 1 表示被装入。问题的解空间是{x1，x2，......xn}，其中 xi = 0 或 xi = 1。

2 确定解空间的组织结构

问题的解空间描述了 2 的 n 次方种可能的解，解空间树为子集树，解空间树的深度为问题的规模 n。

3 搜素解空间

对于任何一个中间节点 z，从根节点到 z 节点的分支所代表的状态已确定，从 z 到其子孙节点的分支状态待确定。也就是说，如果 z 在解空间树中所处的层次是 t，则说明从第 1 种物品到第 t-1 种物品的状态已确定，只需沿着 z 的分支扩展确定第 t 种物品的状态，前 t 种物品的状态就确定了。在前 t 中物品的状态确定后，对当前已转入背包的物品的总重量用 cw 表示，对总价值用 cp 表示。

3.1 约束条件

判断第 i 个物品被装入背包后总重量是否超出背包容量，如果超出，则为不可行解；否则为可行解。约束条件为 cw+w[i]<=W。其中 w[i] 为第 i 个物品的重量，W 为背包容量。

3.2 限界条件

已装入物品的价值高不一定就是最优的，因为还有剩余物品未确定。目前还不确定第 t+1 种物品到第 n 种物品的实际状态，因此只能用估计值。假设第 t+1 种物品到第 n 种物品都被装入背包，对第 t+1 种物品到第 n 种物品的总价值为 rp 来表示。因此 cp+rp 是所有从根出发经过中间节点 z 的可行解的价值上界。如果价值上界小于当前搜索到的最优解，则说明从中间节点 z 继续向子孙节点搜索不可能得到一个比当前更优的可行解。没有继续搜索的必要，反之，继续向 z 的子孙节点搜索。因此限界条件为 cp+rp>=bestp

3.3 搜索过程

从根节点开始，以广度优先的方式进行搜索。根节点首先成为活节点，也就是当前扩展节点。一次性生成所有孩子节点，由于在子集树中约定左子树值为“1”，因此沿着扩展节点左分支扩展，则代表装入物品；由于在子树集中约定右分支的值为“0”，因此沿着扩展节点的右分支扩展，则代表不装入物品。此时判断是否满足约束条件和限界条件，如果满足则加入队列中，反之，则舍弃。然后从队列中取出一个元素，作为当前扩展节点，直到搜索过程队列为空为止。

四图解

有一个背包和 4 个物品，每个物品的重量和价值都如下图所示，背包的容量 W=10,求在不超过背包容量的前提下，把哪些物品放入背包才能获得最大价值。

广度优先搜索算法

1 初始化

sumw 和 sumv 分别用来统计所有物品的总重量和总价值。sumw=13，sumv=18，sumw>W，因此不能全部装完，需搜索求解。初始化当前放入背包的物品价值 cp=0，当前剩余物品价值 rp=sumv=18，当前剩余容量 rw=W，当前处理物品序号为 1 且当前最优值 bestp=0。解向量 x[]=(0,0,0,0)，创建一个根节点 Node(cp,rp,rw,id)，将其标记为 A 并加入队列 q 中。cp 为装入背包的物品价值，rp 为剩余物品的总价值，rw 为剩余容量，id 为物品号，x[] 为当前解向量。

广度优先搜索算法