实现哈夫曼编码（C语言）-Toy模板网

这篇具有很好参考价值的文章主要介绍了实现哈夫曼编码（C语言）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

编译环境：Dev-C++

实现哈夫曼编码的贪心算法实现，并分析哈夫曼编码的算法复杂度。

哈夫曼编码贪心算法的原理如下：

该题目求最小编码长度，即求最优解的问题，可分成几个步骤，一般来说，每个步骤的最优解不一定是整个问题的最优解，然而对于有些问题，局部贪心可以得到全局的最优解。

贪心算法将问题的求解过程看作是一系列选择，从问题的某一个初始解出发，向给定目标推进。推进的每一阶段不是依据某一个固定的递推式，而是在每一个阶段都看上去是一个最优的决策(在一定的标准下)。不断地将问题实例归纳为更小的相似的子问题，并期望做出的局部最优的选择产生一个全局得最优解。
贪心算法适用的问题必须满足两个属性:
①贪心性质:整体的最优解可通过--系列局部最优解达到，并且每次的选择可以依赖以前做出的选择，但不能依赖于以后的选择。
②最优子结构:问题的整体最优解包含着它的子问题的最优解。

        贪心算法的基本步骤：
    ①分解:将原问题分解为若干相互独立的阶段。
    ②解决:对于每一个阶段求局部的最优解。
    ③合并:将各个阶段的解合并为原问题的解。

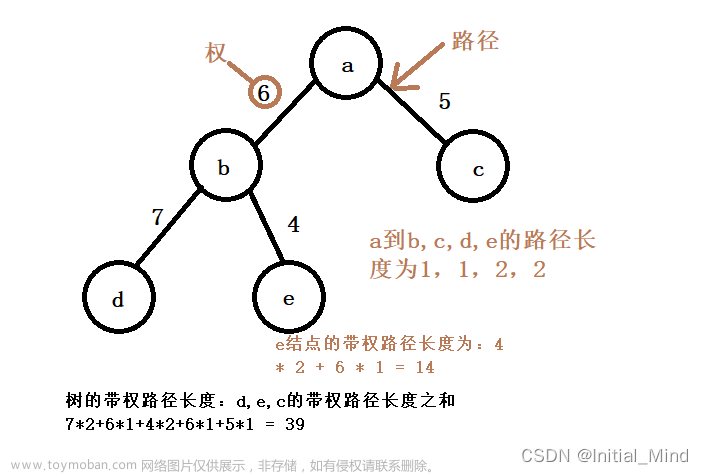
哈夫曼编码实质上是利用最优二叉树原理，求最优前缀码的长度，即平均码长或文件总长最小的前缀编码。计算公式为：

实现哈夫曼编码（C语言）

实质上是让权重越大的编码长度越短，权重越小的编码长度越长。

最优调度动态规划算法的实现步骤如下：

本实验的实现分为两步：先建立哈夫曼树，然后求叶节点的编码。

（1）首先第一步是建立哈夫曼树。

设置一个结构数组 HuffNode 保存哈夫曼树中各结点的信息。根据二叉树的性质可知，具有n个叶子结点的哈夫曼树共有 2n-1 个结点，所以数组 HuffNode 的大小设置为 2n-1 。HuffNode 结构中有 weight, lchild, rchild 和 parent 域。其中，weight 域保存结点的权值, lchild 和 rchild 分别保存该结点的左、右孩子的结点在数组 HuffNode 中的序号，从而建立起结点之间的关系。

为了判定一个结点是否已加入到要建立的哈夫曼树中，可通过 parent 域的值来确定。初始时 parent 的值为 -1。当结点加入到树中去时，该结点 parent 的值为其父结点在数组 HuffNode 中的序号，而不会是 -1 了.

（2）第二步是求叶结点的编码。

该过程实质上就是在已建立的哈夫曼树中，从叶结点开始，沿结点的双亲链域回退到根结点，每回退一步，就走过了哈夫曼树的一个分支，从而得到一位哈夫曼码值。由于一个字符的哈夫曼编码是从根结点到相应叶结点所经过的路径上各分支所组成的 0、1 序列，因此先得到的分支代码为所求编码的低位，后得到的分支代码为所求编码的高位码。

（3）算法实现的流程图

实现哈夫曼编码（C语言）

调试过程及结果

（1）遇到的问题以及解决方法

难点主要在于两个方面：

一是怎么设置哈夫曼树的结构，我一开始打算使用优先队列来做，但后来求出最短路径后无法进行编码，于是改成了数组存储树。然后遇到的困难是数据结构遗忘知识过多，忘记了一个二叉树的节点应该是2*（n-1）+1=2*n-1。浪费了一些时间，后来又去复习数据结构，最后是用数组建立了树的结构，每个节点包括左右节点，根节点，权重4个元素。

二是求叶子节点的遍历，本质上是遍历树。实际上就是一个递推的过程，不断搜寻他的父节点直到根节点（parent=0），如果位于父节点的左侧则为0，右侧则编码1。

写代码的过程中也遇到了一些小问题：

在输入叶子节点的时候，怎么把空格字符去除

想了许多办法，最开始是写了一个trim函数，先读入字符串，然后去除空格再转换为字符数组，后来发现可以直接在输入的地方加一个if语句直接做判断，舍去读入的空格字符。

（2）程序执行的结果。

实现哈夫曼编码（C语言）

复杂度分析：

时间复杂度：因为本实验是通过逐个比较来确定左子树和右子树，所以遍历一遍时间复杂度为O（n），共便利O（n-1）次，所以时间复杂度为O（n*n）。

空间复杂度：实验中申请了一个数组表示树，所以空间复杂度为O（2*n-1）。文章来源地址https://www.toymoban.com/news/detail-419146.html

源代码：

#include<stdio.h>
#include<stdlib.h>
#include<malloc.h>
#define Bit_max 100
#define Value_max 10000
#define Leaf_number_max 5 //叶节点的数量，即要编码的字符的数量(可以修改)
#define Node_number_max Leaf_number_max*2-1 //哈夫曼树总的节点的数量
using namespace std; 

char* leaf=(char *)malloc(sizeof(char)*Leaf_number_max);//叶子节点 
int* leafweight=(int *)malloc(sizeof(int)*Leaf_number_max);//叶子节点的权值 

typedef struct{
    int bit[Bit_max];//字符的哈弗曼编码
    int length;//字符的哈弗曼编码长度
}HCodeType;
/*
	因采用自底向上的编码方式，
    所以事先不知道编码的长度，就统一地设为n-1，
    从后向前填写编码，start表示编码开始的位置
*/
typedef struct{
    int bit[Bit_max];
    int start;
}tmpHCodeType;

typedef struct{
    int weight;
    int parent;
    int lchild;
    int rchild;
}HNodeType;

int n=Leaf_number_max;
HNodeType HuffNode[Node_number_max];//定义全局变量和数组自动初始化
HCodeType HuffCode[Leaf_number_max];
tmpHCodeType cd;

void Init_Input(){
	printf("The number of Leaves are : %d\n",Leaf_number_max);
	puts("The Leaves are : ");
    for(int i=0;i<Leaf_number_max;++i){
		scanf("%c",leaf+i);
		if(*(leaf+i)==' '){
			scanf("%c",leaf+i);
		}else{
			continue;
		}
    }
    puts("The weight of Leaves are : ");
	for(int i=0;i<Leaf_number_max;++i){
		scanf("%d",leafweight+i);
    }
}
void Make_HuffmanTree(){
    int m1, m2;//m1,m2为构造哈夫曼树不同过程中两个最小权值结点的权值
	int Index_1, Index_2;//Index_1,Index_2为构造哈夫曼树不同过程中两个最小权值结点在数组中的序号
    
    //初始化存放哈夫曼数组的结点
    for (int i = 0; i < 2 * n - 1; i++){
        HuffNode[i].weight = 0;
        HuffNode[i].parent = -1;
        HuffNode[i].lchild = -1;
        HuffNode[i].rchild = -1;
    }

    //初始化叶子节点的权值
    for (int i = 0; i < n; i++){
      HuffNode[i].weight=leafweight[i];
    }

    //循环构造哈夫曼树，n个叶子结点需要n-1次构建（将两棵树合并为一棵树）
    for (int i = 0; i < n - 1; i++){
        m1 = m2 = Value_max;
        Index_1 = Index_2 = 0;
        //新建立的节点的下标是原来的叶子总结点数+i即n+i
        for (int j = 0; j < n + i; j++){
            //规定左儿子的权值比右儿子小
            if (HuffNode[j].weight < m1&&HuffNode[j].parent == -1){
                m2 = m1;
                Index_2 = Index_1;
                m1 = HuffNode[j].weight;
                Index_1 = j;
            } else if (HuffNode[j].weight < m2&&HuffNode[j].parent == -1){
                m2 = HuffNode[j].weight;
                Index_2 = j;
            }
        }
        HuffNode[Index_1].parent = n + i;
        HuffNode[Index_2].parent = n + i;
        HuffNode[n + i].weight = HuffNode[Index_1].weight + HuffNode[Index_2].weight;
        HuffNode[n + i].lchild = Index_1;
        HuffNode[n + i].rchild = Index_2;
    }
}

//采用自底向上的编码方式，该节点若是左儿子，则为0，若为右儿子则为1
void HuffmanCode(){
    int c, p;
    for (int i = 0; i < n; i++){
        cd.start = n - 1;//刚开始无法确定该字符的编码长度，因此统一设为n-1
        c = i;//当前节点
        p = HuffNode[c].parent;//当前节点的父节点
        while (p != -1){
            if (HuffNode[p].lchild == c){
                cd.bit[cd.start] = 0;//如果该节点是左儿子
            }else{
                cd.bit[cd.start] = 1;//如果该节点是右儿子
            }
            --cd.start;
            c = p;
            p = HuffNode[c].parent;
        }
        int cnt=0;
        for (int j = cd.start + 1; j < n; j++){
            HuffCode[i].bit[cnt++] = cd.bit[j];
        }
        HuffCode[i].length = cnt;
    }
    //打印各个字符的哈弗曼编码
    for (int i = 0; i < n; i++){
        printf("The Huffman code of \"%c\" is : ", leaf[i]);
        for (int j = 0 ; j <HuffCode[i].length ; j++){
            printf("%d", HuffCode[i].bit[j]);
        }
       putchar('\n'); 
    }
}
int main(){
	Init_Input();
    Make_HuffmanTree();
    HuffmanCode();
    return 0;
}

到了这里，关于实现哈夫曼编码（C语言）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！