类型一：N项和求极限
1.先求和后极限：考的很少，太简单了
首先
推导过程是：
2.夹逼定理：重要的是知道什么时候用夹逼定理，就是当N个项中分母不齐（不齐的意思是有二次项有一次项等）或者分子不齐。
*3.分子次数齐，分母次数齐的同时分母比分子多一次---定积分
4.比如下面这题就是N项的分子全是0次方是整齐的，分母是两项但是全是1次是整齐的，而且分母的1次比分子的0次多一次所以应该用定积分。
5.例题2：
首先要知道反三角函数的导数：
arctanx与tanx关于y=x对称
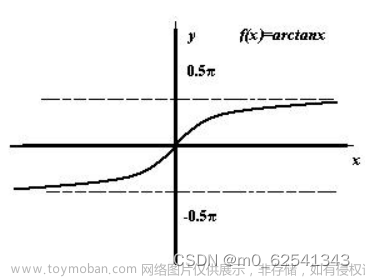
反函数的特殊值：
判断单调数列极限是否存在时的几种题型：
求单调数列（不知道递增还是递减）的极限是否存在的题型：
例题1： 
例题2:
1.证明极限存在，并且求出极限
求出极限：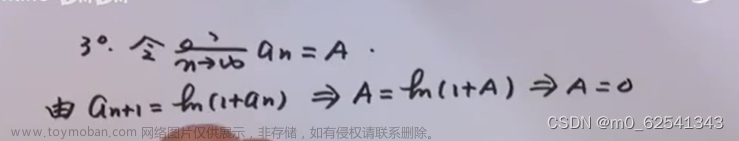
2.求出第二个式子的极限，其中用到了换元法
例题三：首先要知道
基本不等式：(a-b)²≥0,a²+b²-2ab≥0,a²+b²≥2ab.这是基本不等式推导过程。下面是变式：(√a)²+(√b)²≥2√(ab),得a+b≥2√(ab).
套用上面公式，an+1/an≥2√[an×(1/an)]=2，即an+1/an≥2，就是这么来的
极限部分最重要的题型：不定型
总共有七种类型：0/0型和1的无穷次方是最重要的两种类型
0/0型的解题方法有三种：
0/0型的解题习惯：
误区：何时使用等价无穷小----乘除使用等价无穷小是没有问题的，但是在加减的时候使用等价无穷小是需要注意的。
加减法必须在精确度够的时候使用等价无穷小，精确度不够的时候不能使用等价无穷小。如下：
下方的式子的分母因为是乘法使用等价无穷小是没问题的，但是分子是加法，使用等价无穷小后发现，分子和分母都是二阶的，所以精度是一样的，说明这次的加减使用等价无穷小是没有问题的。
再看下方的例子
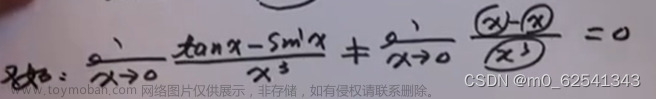
上方图片中的式子的分子是不可以用等价无穷小的，因为用完之后发现分子是一次，而分母是三次，分母的精度是很高的，而分子的精度因为是一次所以很低，所以不可以对分子的加减使用等价无穷小。
正确的做法：文章来源：https://www.toymoban.com/news/detail-419381.html
文章来源地址https://www.toymoban.com/news/detail-419381.html
到了这里，关于极限重要题型讲解（汤家凤B站笔记）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
![[3D&Halcon] 3D重要算子及简单处理点云模型求高度示例讲解](https://imgs.yssmx.com/Uploads/2024/02/776631-1.png)
