🚀write in front🚀
📜所属专栏：初阶数据结构
🛰️博客主页：睿睿的博客主页
🛰️代码仓库：🎉VS2022_C语言仓库
🎡您的点赞、关注、收藏、评论，是对我最大的激励和支持！！！
关注我，关注我，关注我，你们将会看到更多的优质内容！！
前言
在学习完二叉树以后，我们需要通过一些选择题来验收自己的学习成果。本篇博客将通过一些经典选择题带你巩固二叉树的相关性质。
例题1.
答案：A
解析：
A错误: 二叉树指最大孩子个数为2，即树的度为二的树。深度描述的为树的层数。
B正确: 对于任意的树都满足：边的条数比节点个数少1，因为每个节点都有双亲，但是根节点没有
C正确: 正确，参加二叉树性质
D正确: 二叉链一般指孩子表示法，三叉连指孩子双亲表示法，这两种方式是二叉树最常见的表示方式，虽然还有孩子兄弟表示法，该中表示方式本质也是二叉链
例题2.
答案：D
解析：
A: 树中的节点不能相交
B: 树的度为所有节点中度最大的节点的度
C: 树的深度为根节点到叶子节点的最大深度
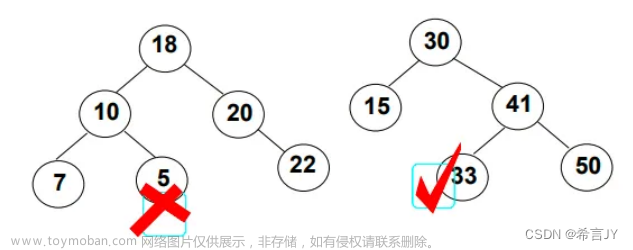
例题3.
答案：C
解析：
通过前序遍历找到子树的根，在中序遍历中找到根的位置，然后确定根左右子树的区间，即根的左侧为左子树中所有节点，根的右侧为右子树中所有节点。
故：根为： 5
5的左子树：4 7 5的右子树： 6 9 1 2
5的左子树的根为: 7 5的右子树的根为：9
7的左子树: 4 7的右：空 9的左子树：6 9的右子树：2
故这棵树的结构为：
例题4.
答案：B
解析：
由后序遍历确定子树的根，后序遍历从后向前看，最后一个元素为根，和前序遍历刚好相反，从后向前看后序遍历，应该是根，右，左，根据中序遍历确定子树的左右区间
故：根为: A
A的左子树：JGDHKB A的右子树：ELIMCF
A的左子树的根：B A的右子树的根：C
B的左子树：JGDHK B的右子树：空 C的左子树：ELIM C的右子树：F
B的左子树的根：D C的左子树根：E
D的左子树的根：G D的右子树的根：H E的右子树的根:I
故树的结构为：
例题5.
答案：C
解析：
前序确定根，中序找到根确定根的左右子树，最后还原二叉树为：
前： ABDEC 中：BDEAC
所以既不是满二叉树，也不是完全二叉树
例题6.
答案：A
解析：
最大深度： 即每次只有一个节点，次数二叉树的高度为n，为最高的高度
最小深度： 此树为完全二叉树， 如果是完全二叉树
根据二叉树性质，完全二叉树的高低为 h = log(n+1)向上取整
故选择A
例题7.
答案：D
解析：
BFS:
广度优先需要把下一步所有可能的位置全部遍历完，才会进行更深层次的遍历，广度优先一般使用队列。层序遍历就是一种广度优先遍历。
DFS：
深度优先是先遍历完一条完整的路径（从根到叶子的完整路径），才会向上层折返，再去遍历下一个路径，深度优先一般使用递归。前序遍历就是一种深度优先遍历。
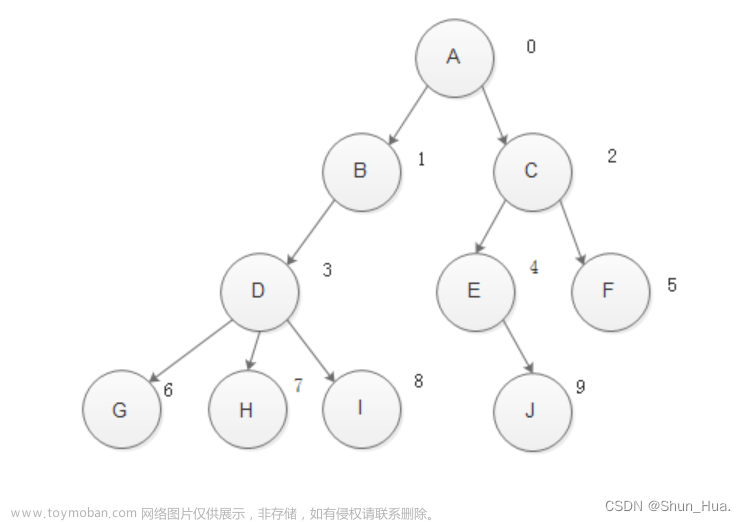
例题8.
答案：B
解析：
首先这棵二叉树的高度一定在3~4层之间:
三层：
A(B(C,D),()), A((),B(C,D)), A(B(C,()),D), A(B((),C),D),
A(B,C(D,())), A(B,C((),D))
四层：
如果为四层，就是单边树，每一层只有一个节点，除过根节点，其他节点都有两种选择，在上层节点的左边还是右边，所以2 * 2 * 2共8种
总共为14种。
例题9.
答案：C
解析：
前序遍历：根 左 右
后序遍历：左 右 根
从二叉树 前序 和 后序遍历结果规则中可以看出，如果树中每个节点只有一个孩子时，遍历结果肯定是反的
比如下面这前序和中序序列所构成的树的结构:
12345
54321
总结
更新不易，辛苦各位小伙伴们动动小手，👍三连走一走💕💕 ~ ~ ~ 你们真的对我很重要！最后，本文仍有许多不足之处，欢迎各位认真读完文章的小伙伴们随时私信交流、批评指正！
专栏订阅：
每日一题
c语言学习
算法
智力题
初阶数据结构
更新不易，辛苦各位小伙伴们动动小手，👍三连走一走💕💕 ~ ~ ~ 你们真的对我很重要！最后，本文仍有许多不足之处，欢迎各位认真读完文章的小伙伴们随时私信交流、批评指正！文章来源：https://www.toymoban.com/news/detail-419612.html
文章来源地址https://www.toymoban.com/news/detail-419612.html
到了这里，关于【数据结构】二叉树性质巩固的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
