Python数据结构与算法篇（五）-- 二分查找与二分答案-Toy模板网

这篇具有很好参考价值的文章主要介绍了Python数据结构与算法篇（五）-- 二分查找与二分答案。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

1 二分法介绍

1.1 定义

二分查找又称折半查找、二分搜索、折半搜索等，是一种在静态查找表中查找特定元素的算法。

所谓静态查找表，即只能对表内的元素做查找和读取操作，不允许插入或删除元素。

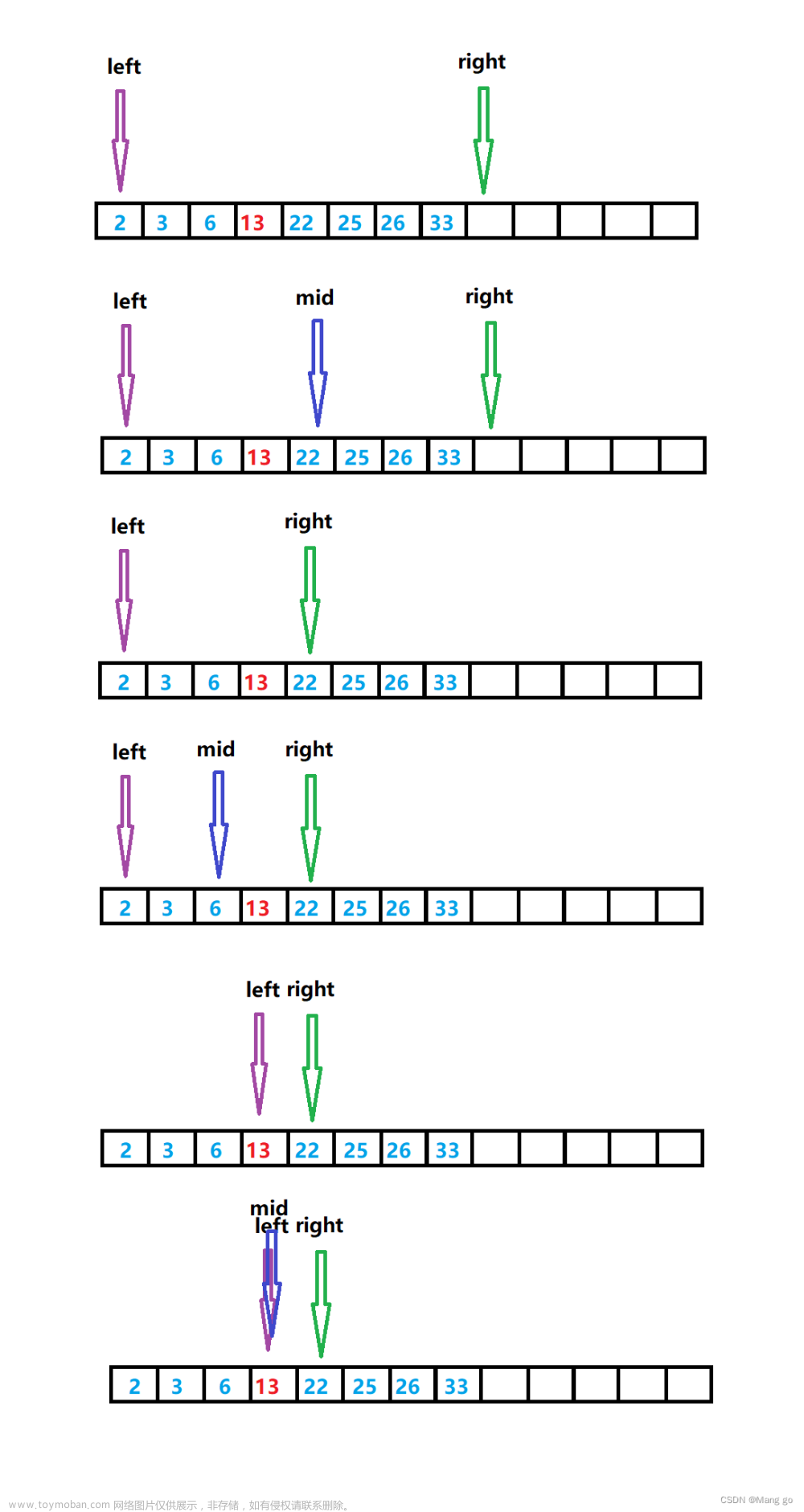
使用二分查找算法，必须保证查找表中存放的是有序序列（升序或者降序）。换句话说，存储无序序列的静态查找表，除非先对数据进行排序，否则不能使用二分查找算法。它针对的是一个有序的数据集合，查找思想有点类似分治思想。每次都通过跟区间的中间元素对比，将待查找的区间缩小为之前的一半，直到找到要查找的元素，或者区间被缩小为 0。下图对比了顺序查找和二分查找的不同：

二分查找的最基本问题是在有序数组里查找一个特定的元素，还可以应用在：

在半有序（旋转有序或者是山脉）数组里查找元素；
确定一个有范围的整数；
需要查找的目标元素满足某个特定的性质。

二分查找算法的时间复杂度可以用 $O(log_2n)$ 表示（ $n$ 为查找表中的元素数量，底数 2 可以省略）。和顺序查找算法的 $O (n)$ 相比，显然二分查找算法的效率更高，且查找表中的元素越多，二分查找算法效率高的优势就越明显。

1.2 二分法的三种写法

1. 模板一

class Solution(object):

    def search(self, nums: List[int], target: int) -> int:
        # 特殊用例判断
        n = len(nums)
        if n == 0:
            return -1
        # 在 [left, right] 区间里查找target
        left, right = 0, n - 1
        while left <= right:
            # 为了防止 left + right 整形溢出，写成如下形式
            # Python 使用 BigInteger，所以不用担心溢出，但还是推荐使用如下方式
            mid = left + (right - left) // 2

            if nums[mid] == target:
                return mid
            elif nums[mid] > target:
                # 下一轮搜索区间：[left, mid - 1]
                right = mid - 1
            else:
                # 此时：nums[mid] < target
                # 下一轮搜索区间：[mid + 1, right]
                left = mid + 1
        return -1

注意事项：

许多刚刚写的朋友，经常在写 left = mid + 1；还是写 right = mid - 1; 感到困惑，一个行之有效的思考策略是：永远去想下一轮目标元素应该在哪个区间里：
- 如果目标元素在区间 [left, mid - 1] 里，就需要设置设置 right = mid - 1；
- 如果目标元素在区间 [mid + 1, right] 里，就需要设置设置 left = mid + 1；

考虑不仔细是初学二分法容易出错的地方，这里切忌跳步，需要仔细想清楚每一行代码的含义。

二分查找算法是典型的「减治思想」的应用，我们使用二分查找将待搜索的区间逐渐缩小，以达到「缩减问题规模」的目的；
循环可以继续的条件是 while (left <= right)，特别地，当 left == right 即当待搜索区间里只有一个元素的时候，查找也必须进行下去；
mid = (left + right) // 2；在 left + right 整形溢出的时候，mid 会变成负数，回避这个问题的办法是写成 mid = left + (right - left) // 2。

2. 模板二

版本一：

def search(nums: List[int], left: int, right: int, target: int) -> int:
    while left < right:
        # 选择中位数时下取整
        mid = left + (right - left) // 2
        if check(mid):
            # 下一轮搜索区间是 [mid + 1, right]
            left = mid + 1
        else:
            # 下一轮搜索区间是 [left, mid]
            right = mid
    # 退出循环的时候，程序只剩下一个元素没有看到。
    # 视情况，是否需要单独判断 left（或者 right）这个下标的元素是否符合题意

版本二：

def search(nums: List[int], left: int, right: int, target: int) -> int:
    while left < right:
        # 选择中位数时上取整
        mid = left + (right - left + 1) // 2
        if check(mid):
            # 下一轮搜索区间是 [left, mid - 1]
            right = mid - 1
        else:
            # 下一轮搜索区间是 [mid, right]
            left = mid
    # 退出循环的时候，程序只剩下一个元素没有看到。
    # 视情况，是否需要单独判断 left（或者 right）这个下标的元素是否符合题意

理解模板代码的要点：

核心思想：虽然模板有两个，但是核心思想只有一个，那就是：把待搜索的目标元素放在最后判断，每一次循环排除掉不存在目标元素的区间，目的依然是确定下一轮搜索的区间；
特征：while (left < right):，这里使用严格小于 < 表示的临界条件是：当区间里的元素只有 2 个时，依然可以执行循环体。换句话说，退出循环的时候一定有 left == right成立，这一点在定位元素下标的时候极其有用；
在循环体中，先考虑 nums[mid] 在满足什么条件下不是目标元素，进而考虑两个区间 [left, mid - 1] 以及 [mid + 1, right] 里元素的性质，目的依然是确定下一轮搜索的区间； 注意 1： 先考虑什么时候不是解，是一个经验，在绝大多数情况下不易出错，重点还是确定下一轮搜索的区间，由于这一步不容易出错，它的反面（也就是 else 语句的部分），就不用去考虑对应的区间是什么，直接从上一个分支的反面区间得到，进而确定边界如何设置；
根据边界情况，看取中间数的时候是否需要上取整； 注意 2： 这一步也依然是根据经验，建议先不要记住结论，在使用这个思想解决问题的过程中，去思考可能产生死循环的原因，进而理解什么时候需要在括号里加 1 ，什么时候不需要；
在退出循环以后，根据情况看是否需要对下标为 left 或者 right 的元素进行单独判断，这一步叫「后处理」。在有些问题中，排除掉所有不符合要求的元素以后，剩下的那 1 个元素就一定是目标元素。如果根据问题的场景，目标元素一定在搜索区间里，那么退出循环以后，可以直接返回 left（或者 right）。

以上是这两个模板写法的所有要点，并且是高度概括的。请读者一定先抓住这个模板的核心思想，在具体使用的过程中，不断地去体会这个模板使用的细节和好处。只要把中间最难理解的部分吃透，几乎所有的二分问题就都可以使用这个模板来解决，因为「减治思想」是通用的。好处在这一小节的开篇介绍过了，需要考虑的细节最少。

学习建议：一定需要多做练习，体会这（两）个模板的使用。

注意事项：

先写分支，再决定中间数是否上取整；
在使用多了以后，就很容易记住，只要看到 left = mid ，它对应的取中位数的取法一定是 mid = left + (right - left + 1) // 2。

3. 模板三

def search(nums: List[int], left: int, right: int, target: int) -> int:
    while left + 1 < right:
        # 选择中位数时下取整
        mid = left + (right - left) // 2
        if nums[mid] == target:
            return mid
        elif nums[mid] < target:
            left = mid
        else:
            right = mid

    if nums[left] == target:
        return left
    if nums[right] == target:
        return right
    return -1

这一版代码和模板二没有本质区别，一个显著的标志是：循环可以继续的条件是 while (left + 1 < right):，这说明在退出循环的时候，一定有 left + 1 == right 成立，也就是退出循环以后，区间有 2 个元素，即 [left, right]；
这种写法的优点是：不用理解上一个版本在分支出现 left = mid 的时候中间数上取整的行为；
缺点是显而易见的：
- while (left + 1 < right): 写法相对于 while (left < right): 和 while (left <= right): 来说并不自然；
- 由于退出循环以后，区间一定有两个元素，需要思考哪一个元素才是需要找的，即「后处理」一定要做，有些时候还会有先考虑 left 还是 right 的区别。

小结：

模板一：最好理解的版本，但是在刷题的过程中，需要处理一些边界的问题，一不小心容易出错；
模板二：强烈推荐掌握的版本，应先理解思想，再通过实际应用去体会这个模板的细节，熟练使用以后就会觉得非常自然；
模板三：可以认为是模板二的避免踩坑版本，只要深刻理解了模板二，模板三就不在话下。

实际应用中，选择最好理解的版本即可。

这里有一个提示：模板二考虑的细节最少，可以用于解决一些相对复杂的问题。缺点是：学习成本较高，初学的时候比较容易陷入死循环，建议大家通过多多使用，并且尝试 debug，找到死循环的原因，进而掌握。

题解核心内容：所有模板都一样，不可以套模板，而应该仔细看题（解题的关键在认真读题），分析清楚题目要找的答案需要满足什么性质。采用两边夹的方式，每一轮把待搜索区间分成两个部分，排除掉一定不是答案的区间，最后左右指针重合的地方就是我们要找的元素。一定要分析清楚题目的意思，分析清楚要找的答案需要满足什么性质。应该清楚模板具体的用法，明白需要根据题意灵活处理、需要变通的地方，不可以认为每一行代码都是模板规定死的写法，不可以盲目套用、死记硬背。

2 常见题型

2.1 二分求下标（在数组中查找符合条件的元素的下标）

题库列表

题号	链接
704	二分查找（简单）
35	搜索插入位置（简单）
300	最长上升子序列（中等）
34	在排序数组中查找元素的第一个和最后一个位置（简单）
611	有效三角形的个数
436	寻找右区间（中等）
4	寻找两个有序数组的中位数（困难）

2.2 完全有序

704. 二分查找
题目描述：给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

# lower_bound 返回最小的满足 nums[i] >= target 的 i
# 如果数组为空，或者所有数都 < target，则返回 len(nums)
# 要求 nums 是非递减的，即 nums[i] <= nums[i + 1]

# 闭区间写法
def lower_bound(nums: List[int], target: int) -> int:
    left, right = 0, len(nums) - 1  # 闭区间 [left, right]
    while left <= right:  # 区间不为空
        # 循环不变量：
        # nums[left-1] < target
        # nums[right+1] >= target
        mid = (left + right) // 2
        if nums[mid] < target:
            left = mid + 1      # 范围缩小到 [mid+1, right]
        else:
            right = mid - 1     # 范围缩小到 [left, mid-1]
    return left                 # 或者 right+1

# 左闭右开区间写法
def lower_bound2(nums: List[int], target: int) -> int:
    left, right = 0, len(nums)  # 左闭右开区间 [left, right)
    while left < right:  # 区间不为空
        # 循环不变量：
        # nums[left-1] < target
        # nums[right] >= target
        mid = (left + right) // 2
        if nums[mid] < target:
            left = mid + 1  # 范围缩小到 [mid+1, right)
        else:
            right = mid  # 范围缩小到 [left, mid)
    return left  # 或者 right

# 开区间写法
def lower_bound3(nums: List[int], target: int) -> int:
    left, right = -1, len(nums)  # 开区间 (left, right)
    while left + 1 < right:  # 区间不为空
        mid = (left + right) // 2
        # 循环不变量：
        # nums[left] < target
        # nums[right] >= target
        if nums[mid] < target:
            left = mid  # 范围缩小到 (mid, right)
        else:
            right = mid  # 范围缩小到 (left, mid)
    return right  # 或者 left+1

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        i = lower_bound(nums, target)  # 选择其中一种写法即可
        return i if i < len(nums) and nums[i] == target else -1

35. 搜索插入位置

题目描述：给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

class Solution:
    def searchInsert(self, nums: List[int], target: int) -> int:
        left, right = 0, len(nums) - 1
        while left <= right:
            mid = (left + right) // 2
            if nums[mid] == target:
                return mid
            elif nums[mid] < target:
                left = mid + 1
            else:
                right = mid - 1
        return left

class Solution:
    def searchInsert(self, nums: List[int], target: int) -> int:
        left, right = 0, len(nums)          # 采用左闭右开区间[left,right)
        while left < right:                 # 右开所以不能有=,区间不存在
            mid = left + (right - left)//2  # 防止溢出, //表示整除
            if nums[mid] < target:          # 中点小于目标值,在右侧,可以得到相等位置
                left = mid + 1              # 左闭, 所以要+1
            else:
                right = mid                 # 右开, 真正右端点为mid-1
        return left                         # 此算法结束时保证left = right, 返回谁都一样

300. 最长上升子序列
题目描述：给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。子序列是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

1. 动态规划 + 二分查找

# Dynamic programming + Dichotomy.
class Solution:
    def lengthOfLIS(self, nums: [int]) -> int:
        tails, res = [0] * len(nums), 0
        for num in nums:
            i, j = 0, res
            while i < j:
                m = (i + j) // 2
                if tails[m] < num: 
                    i = m + 1           # 如果要求非严格递增，将此行 '<' 改为 '<=' 即可。
                else: 
                    j = m
            tails[i] = num
            if j == res: 
                res += 1
        return res

2. 动态规划

class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        if not nums: return 0
        dp = [1] * len(nums)
        for i in range(len(nums)):
            for j in range(i):
                if nums[j] < nums[i]: # 如果要求非严格递增，将此行 '<' 改为 '<=' 即可。
                    dp[i] = max(dp[i], dp[j] + 1)
        return max(dp)

34. 在排序数组中查找元素的第一个和最后一个位置

题目描述：给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。如果数组中不存在目标值 target，返回 [-1, -1]。

class Solution:
    def searchRange(self, nums: List[int], target: int) -> List[int]:
        if not nums or target not in nums:          # 特例，二分查找失败
            return [-1, -1]
        return [self.lower_bound(nums, target), self.upper_bound(nums, target)]

    def upper_bound(self, nums: List[int], target: int):    # 寻找上边界
        left, right = 0, len(nums)-1
        while left <= right:
            mid = left + (right - left) // 2
            if nums[mid] <= target:     # 移动左指针
                left = mid + 1
            else:                       # 移动右指针
                right = mid -1
        return right


    def lower_bound(self, nums: List[int], target: int):    # 寻找下边界
        left, right = 0, len(nums)-1
        while left <= right:
            mid = left + (right - left) // 2
            if nums[mid] >= target:         # 当nums[mid]大于等于目标值时，继续在左区间检索，找到第一个数
                right = mid - 1
            else:           # nums[mid]小于目标值时，则在右区间继续检索，找到第一个等于目标值的数
                left = mid + 1
        return left

611. 有效三角形的个数
题目描述：给定一个包含非负整数的数组 nums ，返回其中可以组成三角形三条边的三元组个数。

将数组 nums 进行升序排序，随后使用二重循环枚举 a 和 b。设 $a = n u m s [i], b = n u m s [j]$ ，为了防止重复统计答案，我们需要保证 $i < j$ 。剩余的边 c 需要满足 $c < n u m s [i] + n u m s [j]$ ，我们可以在 $[j + 1, n - 1]$ 的下标范围内使用二分查找（其中 $n$ 是数组 nums 的长度），找出最大的满足 $n u m s [k] < n u m s [i] + n u m s [j]$ 的下标 $k$ ，这样一来，在 $[j + 1, k]$ 范围内的下标都可以作为边 $c$ 的下标，我们将该范围的长度 $k - j$ 累加入答案。

1. 排序+二分查找

class Solution:
    def triangleNumber(self, nums: List[int]) -> int:
        nums.sort()
        length = len(nums)
        ans = 0
        for i in range(length):
            for j in range(i+1, length):
                left, right = j+1, length              
                while left < right:             # 找边界，
                    mid = (left + right)//2
                    if nums[mid] < nums[i] + nums[j]:
                        left = mid + 1
                    else:
                        right = mid
                ans += left - 1 - j
        return ans

2. 排序+双指针

我们将当 $a = n u m s [i], b = n u m s [j]$ 时，最大的满足 $n u m s [k] < n u m s [i] + n u m s [j]$ 的下标 $k$ 记为 $k_{i,j}$ 。可以发现，如果我们固定 $i$ ，那么随着 $j$ 的递增，不等式右侧 $n u m s [i] + n u m s [j]$ 也是递增的，因此 $k_{i,j}$ 也是递增的。

这样一来，我们就可以将 $j$ 和 $k$ 看成两个同向（递增）移动的指针，将方法一进行如下的优化：

我们使用一重循环枚举 $i$ 。当 $i$ 固定时，我们使用双指针同时维护 $j$ 和 $k$ ，它们的初始值均为 $i$ ；
我们每一次将 $j$ 向右移动一个位置，即 $j \leftarrow j + 1$ ，并尝试不断向右移动 $k$ ，使得 $k$ 是最大的满足 $n u m s [k] < n u m s [i] + n u m s [j]$ 的下标。我们将 $ma x (k - j, 0)$ 累加入答案。

class Solution:
    def triangleNumber(self, nums: List[int]) -> int:
        nums.sort()
        length = len(nums)
        ans = 0
        for i in range(length):
            k = i + 1 
            for j in range(i+1, length):
                while k+1 < length and nums[i] + nums[j] > nums[k+1]:
                    k += 1
                ans += max(k-j, 0)
        return ans

436. 寻找右区间
题目描述：
Python数据结构与算法篇（五）-- 二分查找与二分答案

class Solution:
    def findRightInterval(self, intervals: List[List[int]]) -> List[int]:
        start_map = {interval[0] : i for i, interval in enumerate(intervals)}       # 以区间左侧构建索引字典
        starts = [interval[0] for interval in intervals]                            # 取出区间的左侧
        res = []
        starts.sort()
        for interval in intervals:
            pos = self.higher_find(starts, interval[1])                             # 遍历每个区间的右侧，在所有区间的左侧进行二分查找
            res.append(start_map[starts[pos]] if pos != -1 else -1)
        return res
    
    def higher_find(self, nums, target):
        left, right = 0, len(nums)              # 左闭右开
        while left < right:
            mid = left + (right - left) // 2
            if nums[mid] >= target:
                right = mid
            else:
                left = mid + 1
        if left < len(nums) and nums[left] >= target:    # 最后判断一下，是否满足条件
            return left
        return -1

4. 寻找两个正序数组的中位数

题目描述：给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的中位数。算法的时间复杂度应该为 $O (l o g (m + n))$ 。

class Solution:
    def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
        def getKthElement(k):
            """
            - 主要思路：要找到第 k (k>1) 小的元素，那么就取 pivot1 = nums1[k/2-1] 和 pivot2 = nums2[k/2-1] 进行比较
            - 这里的 "/" 表示整除
            - nums1 中小于等于 pivot1 的元素有 nums1[0 .. k/2-2] 共计 k/2-1 个
            - nums2 中小于等于 pivot2 的元素有 nums2[0 .. k/2-2] 共计 k/2-1 个
            - 取 pivot = min(pivot1, pivot2)，两个数组中小于等于 pivot 的元素共计不会超过 (k/2-1) + (k/2-1) <= k-2 个
            - 这样 pivot 本身最大也只能是第 k-1 小的元素
            - 如果 pivot = pivot1，那么 nums1[0 .. k/2-1] 都不可能是第 k 小的元素。把这些元素全部 "删除"，剩下的作为新的 nums1 数组
            - 如果 pivot = pivot2，那么 nums2[0 .. k/2-1] 都不可能是第 k 小的元素。把这些元素全部 "删除"，剩下的作为新的 nums2 数组
            - 由于我们 "删除" 了一些元素（这些元素都比第 k 小的元素要小），因此需要修改 k 的值，减去删除的数的个数
            """
            
            index1, index2 = 0, 0
            while True:
                # 特殊情况
                if index1 == m:
                    return nums2[index2 + k - 1]
                if index2 == n:
                    return nums1[index1 + k - 1]
                if k == 1:
                    return min(nums1[index1], nums2[index2])

                # 正常情况
                newIndex1 = min(index1 + k // 2 - 1, m - 1)
                newIndex2 = min(index2 + k // 2 - 1, n - 1)
                pivot1, pivot2 = nums1[newIndex1], nums2[newIndex2]
                if pivot1 <= pivot2:
                    k -= newIndex1 - index1 + 1
                    index1 = newIndex1 + 1
                else:
                    k -= newIndex2 - index2 + 1
                    index2 = newIndex2 + 1
        
        m, n = len(nums1), len(nums2)
        totalLength = m + n
        if totalLength % 2 == 1:
            return getKthElement((totalLength + 1) // 2)
        else:
            return (getKthElement(totalLength // 2) + getKthElement(totalLength // 2 + 1)) / 2

2.3 不完全有序

题库列表：

题号	链接
33	搜索旋转排序数组（中等）
81	搜索旋转排序数组 II（中等）
153	寻找旋转排序数组中的最小值（中等）
154	寻找旋转排序数组中的最小值 II（困难）
852	山脉数组的峰顶索引（简单）
1095	山脉数组中查找目标值（中等）

33. 搜索旋转排序数组

题目描述：整数数组 nums 按升序排列，数组中的值互不相同。在传递给函数之前，nums 在预先未知的某个下标 $k (0 <= k < n u m s . l e n g t h)$ 上进行了旋转，使数组变为 $[n u m s [k], n u m s [k + 1], ..., n u m s [n - 1], n u m s [0], n u m s [1], ..., n u m s [k - 1]]$ （下标从0开始计数）。例如，[0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。给你旋转后的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1。

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        left, right = 0, len(nums)-1
        while left <= right:
            mid = (left + right) // 2
            if nums[mid] == target:
                return mid
            if nums[mid] >= nums[left]:                        # 左半部分有序
                if nums[0] <= target < nums[mid]:           # target 在左半部分
                    right = mid - 1
                else:
                    left = mid + 1
            else:                                           # 右半部分有序
                if nums[mid] < target <= nums[len(nums)-1]: # target 在右半部分
                    left = mid + 1
                else:
                    right = mid - 1
        return -1

81. 搜索旋转排序数组 II

题目描述：

class Solution:
    def search(self, nums: List[int], target: int) -> bool:
        left, right = 0, len(nums)-1
        while left <= right:
            mid = (left + right)//2
            if nums[mid] == target:
                return True
            if nums[mid] == nums[left]:         # 去重
                left += 1
                continue
            if nums[left] <= nums[mid]:        # 左半部分有序，在左侧二分查找
                if nums[left] <= target < nums[mid]:
                    right = mid - 1
                else:
                    left = mid + 1
            else:                               # 右半部分有序，在右侧二分查找
                if  nums[mid] < target <= nums[right]:
                    left = mid + 1
                else:
                    right = mid - 1
        return False

153. 寻找旋转排序数组中的最小值

题目描述：

class Solution:
    def findMin(self, nums: List[int]) -> int:    
        low, high = 0, len(nums) - 1
        while low < high:
            pivot = low + (high - low) // 2
            if nums[pivot] < nums[high]:
                high = pivot 
            else:
                low = pivot + 1
        return nums[low]

154. 寻找旋转排序数组中的最小值 II

题目描述：

class Solution:
    def findMin(self, nums: List[int]) -> int:
        left, right = 0, len(nums)-1
        while left < right:
            mid = (left+right) // 2
            if nums[mid] < nums[right]:
                right = mid
            elif nums[mid] > nums[right]:
                left = mid + 1
            else:
                right -= 1              # 去重
        return nums[left]

852. 山脉数组的峰顶索引（简单）

题目描述：

1. 顺序查找

class Solution:
    def peakIndexInMountainArray(self, arr: List[int]) -> int:
        # 顺序查找最大值
        for i in range(1, len(arr) - 1):
            if arr[i] > arr[i + 1]:
                return i

2. 二分查找

class Solution:
    def peakIndexInMountainArray(self, arr: List[int]) -> int:
        # 二分查找最大值
        left, right = 0, len(arr) - 1
        while left < right:
            mid = (left + right) // 2
            if arr[mid] > arr[mid + 1]:
                right = mid
            else:
                left = mid + 1
        return left

1095. 山脉数组中查找目标值

题目描述：

class Solution:
    def findInMountainArray(self, target: int, mountain_arr: 'MountainArray') -> int:
        '''
        先使用二分法找到数组的峰值。
        在峰值左边使用二分法寻找目标值。
        如果峰值左边没有目标值，那么使用二分法在峰值右边寻找目标值。
        '''
        head, tail = 0, mountain_arr.length()-1
        while head < tail:             # 找峰值，注意越界处理
            mid = (head+tail)//2
            if mountain_arr.get(mid) < mountain_arr.get(mid+1):
                head = mid + 1
            else:
                tail = mid
        peak = head
        ans = self.binarySearch(mountain_arr, target, 0, peak)                                              # 在左半边搜索
        if ans != -1:
            return ans
        return self.binarySearch(mountain_arr, target, peak+1, mountain_arr.length()-1, lambda x:-x)        # 在右半边搜索
    

    def binarySearch(self, mountain, target, left, right, key=lambda x: x): 
        target = key(target)                            # 这里的key相当于把两边全部转为升序部分，也可以用target*reverse，根据reverse的正负来判断
        while left <= right:
            mid = (left + right) // 2
            curr = key(mountain.get(mid))
            if curr == target:
                return mid
            elif curr < target:
                left = mid + 1
            else:
                right = mid - 1
        return -1

2.4 二分答案（在一个有范围的区间里搜索一个整数）

如果题目要我们找一个整数，这个整数有确定的范围，可以通过二分查找逐渐缩小范围，最后逼近到一个数。

定位一个有范围的整数，这件事情也叫「二分答案」或者叫「二分结果」。如果题目要求的是一个整数，这个整数有明确的范围，可以考虑使用二分查找。

题号	链接
69	x 的平方根（简单）
287	寻找重复数（中等）
374	猜数字大小（简单）

69. x 的平方根

题目描述：给你一个非负整数 x ，计算并返回 x 的算术平方根。由于返回类型是整数，结果只保留整数部分，小数部分将被舍去。

class Solution:
    def mySqrt(self, x: int) -> int:
        left, right= 0, x//2
        while left <= right:
            mid = (left + right) // 2
            if mid * mid == x:
                return mid
            if mid * mid < x:
                left = mid + 1
            else:
                right = mid - 1
        return left if left ** 2 <= x else left-1

287. 寻找重复数

题目描述：给定一个包含 $n + 1$ 个整数的数组 nums ，其数字都在 $[1, n]$ 范围内（包括 1 和 n），可知至少存在一个重复的整数。假设 nums 只有一个重复的整数，返回这个重复的数。你设计的解决方案必须不修改数组 nums 且只用常量级 $O (1)$ 的额外空间。

1. 二分法

设数组长度为nnn，则数组中元素 $\in[1, n-1]$ ，且只有一个重复元素。一个直观的想法，设一个数字 $k\in[1,n-1]$ ，统计数组中小于等于 $k$ 的数字的个数 count：

若 $co u n t <= k$ ，说明重复数字一定在 $(k, n - 1]$ 的范围内。
若 $co u n t > k$ ，说明重复数字一定在 $[0, k]$ 的范围内。
利用这个性质，我们使用二分查找逐渐缩小重复数字所在的范围。

初试化左右数字边界 $l e f t = 1, r i g h t = n - 1$
循环条件 $l e f t < r i g h t :$
- $mi d = (l e f t + r i g h t) //2$
- 按照性质，统计数组中小于等于 $mi d$ 的元素个数 $co u n t$
- 若 $co u n t <= mi d$ ，说明重复数字一定在 $(mi d, r i g h t]$ 的范围内。令 $l e f t = mi d + 1$
- 若 $co u n t > mi d$ ，说明重复数字一定在 $[l e f t, mi d]$ 的范围内。令 $r i g h t = mi d$ 。
返回 $l e f t$

class Solution:
    def findDuplicate(self, nums: List[int]) -> int:
        left = 1
        right = len(nums) - 1
        while(left<right):
            mid=(left+right)//2
            count=0
            for num in nums:
                if(num<=mid):
                    count+=1
            if(count<=mid):
                left=mid+1
            else:
                right=mid
        return left

2. 快慢指针

分为两步：

找到环
找到环的入口（即重复元素）

找环：

定义快慢指针 $s l o w = 0, f a s t = 0$
进入循环：
- $s l o w$ 每次走一步，即 $s l o w = n u m s [s l o w]$
- $f a s t$ 每次走两步，即 $f a s t = n u m s [n u m s [f a s t]]$
- 当 $s l o w == f a s t$ 时，退出循环。当快慢指针相遇时，一定在环内。此时假设slow 走了 $k$ 步，则 fast 走了 $2 k$ 步。设环的周长为 $c$ ，则 $k$ 。
找环的入口：
定义新的指针 $f in d = 0$
进入循环：
- find 每次走一步，即 $f in d = n u m s [f in d]$
- slow每次走一步，即 $s l o w = n u m s [s l o w]$
- 当两指针相遇时，即 $f in d == s l o w$ ，返回 find

为何相遇时，找到的就是入口：假设起点到环的入口(重复元素)，需要 $m$ 步。此时 slow 走了 $n + m$ 步，其中 $n$ 是环的周长 $c$ 的整数倍，所以相当于 slow走了 $m$ 步到达入口，再走了 $n$ 步。所以相遇时一定是环的入口。

class Solution:
    def findDuplicate(self, nums: List[int]) -> int:
        slow=0
        fast=0
        while(1):
            slow=nums[slow]
            fast=nums[nums[fast]]
            if(slow==fast):
                break
        find=0
        while(1):
            find=nums[find]
            slow=nums[slow]
            if(find==slow):
                return find

374. 猜数字大小

题目描述：
Python数据结构与算法篇（五）-- 二分查找与二分答案

# The guess API is already defined for you.
# @param num, your guess
# @return -1 if num is higher than the picked number
#          1 if num is lower than the picked number
#          otherwise return 0
# def guess(num: int) -> int:

class Solution:
    def guessNumber(self, n: int) -> int:
        left, right = 0, n
        while left <= right:
            mid = left + ((right-left)>>1)
            temp = guess(mid)
            if temp == 0:
                return mid
            elif temp == 1:
                left = mid + 1
            else:
                right = mid -1

小结

二分法暂时告一段落，后面在学习中持续补充，谢谢大家的鼓励和支持！文章来源地址https://www.toymoban.com/news/detail-419751.html

参考

二分查找算法：https://ojeveryday.github.io/AlgoWiki/#/BinarySearch/README
二分算法：https://oi-wiki.org/basic/binary/
二分查找：https://www.cnblogs.com/jasonbourne3/p/17141780.html
算法与数据结构（七）：二分查找法总结：https://blog.csdn.net/Dby_freedom/article/details/94332149
一文带你搞定二分查找及其多个变种：https://leetcode.cn/problems/find-first-and-last-position-of-element-in-sorted-array/solution/
写对二分查找不是套模板并往里面填空，需要仔细分析题意：https://leetcode.cn/problems/search-insert-position/solutions/10969/te-bie-hao-yong-de-er-fen-cha-fa-fa-mo-ban-python-/
二分查找（折半查找）算法详解：http://data.biancheng.net/view/336.html

到了这里，关于Python数据结构与算法篇（五）-- 二分查找与二分答案的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！