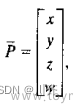机器人学基础(1)位置运动学:正运动学、逆运动学方程建立及其求解
机器人学基础学了个知识框架入门,以此来写一下总结笔记,便于以后要用到相关知识点进行翻阅。
本次机器人学基础笔记主要分为几个章节:位置运动学、微分运动和速度、动力学分析和力、轨迹规划。
后续其他的知识点等学到了再进行补充。
本人也是刚入门学习,还有很多不足还望大家多多指点!
机器人学基础知识点框架:

主要学习资料
1、b站台大林沛群老师课程
https://www.bilibili.com/video/BV1v4411H7ez/?spm_id_from=333.1007.top_right_bar_window_custom_collection.content.click&vd_source=41e646f94a8a699c1dff7daee76f3787
2、机器人学导论 分析、控制及应用 第2版 (Saeed B. Niku)
3、机器人学导论(原书第4版) (John J. Craig 贠超 王伟)
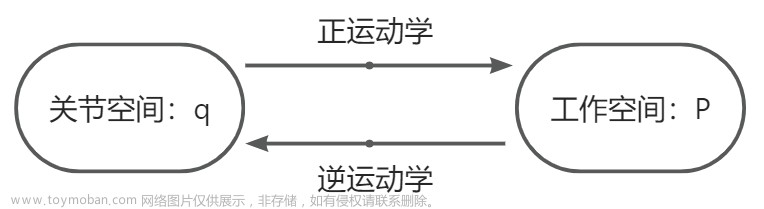
一、正运动学
正运动学可以理解为,已知机械臂各个关节θ,求机械臂手末端的位置和姿态。
1、D-H法
正运动学方程有很多其他的表示方法,D-H法、改进D-H法等,这里主要讲述D-H法。
参考CSDN:
https://blog.csdn.net/huangjunsheng123/article/details/109278122?utm_medium=distribute.pc_relevant.none-task-blog-2defaultbaidujs_utm_term~default-1-109278122-blog-104766458.pc_relevant_3mothn_strategy_recovery&spm=1001.2101.3001.4242.2&utm_relevant_index=4
参考b站林沛群老师课程
D-H法不仅用于表示机械臂的构造,最主要的好处是微分运动学、雅可比分析、动力学分析及力分析等都是基于D-H表示获得的结果
2、矩阵变换
矩阵变换左乘和右乘的含义:绕固定坐标系旋转时,左乘旋转矩阵;绕自身坐标系旋转时,右乘旋转矩阵。
D-H表示法是进行右乘旋转矩阵,因为D-H是绕自身坐标系旋转,而不是绕基座的坐标系。
参考CSDN:https://blog.csdn.net/weixin_45632220/article/details/117735223?spm=1001.2014.3001.5506
其中涉及到的直角(台架)坐标、圆柱坐标、球坐标、链式(拟人或全旋转)坐标,滚动角、俯仰角、偏航角、欧拉角、链式关节的变换,这里就不展开描述,具体参考:机器人学导论 分析、控制及应用 第2版 (Saeed B. Niku)
3、例题


二、逆运动学
逆运动学可以理解为,已知机械臂末端的位置和姿态,求机械臂各个关节θ
1、逆运动学求解
逆运动学求解方法有解析求解和数值求解。
解析求解有代数求解和几何求解,数值求解有牛顿-拉风森法。
本文主要讲解的方法为解析求解中的代数求解,几何求解需画几何图进行求解较为少用,数值求解本人还未怎么学习到,等学习了再来补上知识点。





代数求解方法具体参考 机器人学导论 分析、控制及应用 第2版 (Saeed B. Niku)
2、逆运动学一般解
若采用代数求解法来求解运动方程,每次都要跟上述步骤一样显得十分的麻烦,所以对于结构相同的机械臂,逆运动学求解出来的各关节θ存在一般解。


对于斯坦福机械臂结构来说,每次进行求解时使用上述的公式即可,进行编程时也是一样
总结
掌握正运动学概念、矩阵变换、正运动学方程建立及求得最终机械臂末端的位置和姿态矩阵
掌握逆运动学概念、代数求解、掌握机械臂的一般解表示方法,掌握斯坦福机械臂的一般解
对于坐标系矩阵变换的直角(台架)坐标、圆柱坐标、球坐标、链式(拟人或全旋转)坐标,滚动角、俯仰角、偏航角、欧拉角、链式关节等仍不熟悉,后续可进行翻阅课本学习
对于逆运动学求解的数值求解方法未掌握,后续需要深入研究时再进行学习文章来源:https://www.toymoban.com/news/detail-420072.html
若需要电子版书籍、ppt资料等可私信或评论进行获取文章来源地址https://www.toymoban.com/news/detail-420072.html
到了这里,关于机器人学基础(1)-位置运动学-正运动学、逆运动学方程建立及其求解的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!