概率密度函数曲线及绘制-Toy模板网

这篇具有很好参考价值的文章主要介绍了概率密度函数曲线及绘制。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

前言

很多数据科学家在做回归模型评估的时候，不仅会去计算模型拟合优度R2，平均绝对误差还会去看测试集的每个样本偏差的分布情况，这个时候就需要用到概率密度函数曲线的知识了，通过绘制概率密度函数曲线图或者直方图可以很直观的看到测试集的所有样本的偏差分布情况。

概率密度函数曲线

我们知道概率是用来度量一件事物发生可能性大小，以抛色子为例，一枚色子是一个正六面体，一共6个面，分别标有1～6，随手一抛，求出现点数5朝上的可能性是多少？因为样本空间数是6，对点数5朝上的有利事件数是1（点数5朝上），因此，出现点数5朝上的概率都是1/6，这是古典概率论的描述，列出其概率分步表如下

点数	1	2	3	4	5	6
概率	1/6	1/6	1/6	1/6	1/6	1/6

画出其概率分布图如下
概率密度函数曲线及绘制

对于有限离散的样本空间，我们可以列出概率分布表画出概率分布图，如果，某事件可能取值是某个连续的区间 $[a, b]$ ，也有其对应的概率值，这种对应关系称为连续型概率函数，记作

$x\in[a,b]$

其中，p表示自变量取x附近一小段的概率，对应的概率分布函数图像可以用一条连续的曲线来刻画
概率密度函数曲线及绘制
其中，横坐标表示自变量x取值范围，从a到b，可以是a,b中间某一点或某一小段或几个小段的并等，纵坐标表示因变量f(x)取值大小，可以得到

$\int_{a}^{a} f(x) dx = 1$

这样，概率函数可以定义为连续型随机变量(X)在某个确定的取值点附近的可能性的函数，可以类比一个质地不均匀的橡皮泥横梗在a，b之间，如果要求这块橡皮泥的质量，那么就要知道从a到b的各处的密度大小，所以概率函数也叫概率密度函数。

几类经典的概率密度函数

正态分布

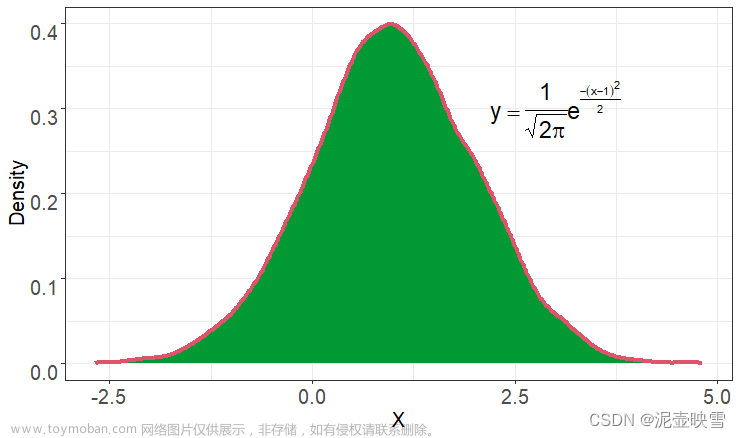
正态分布是最常见的一种的概率分布，也称为也称为高斯分布，它刻画了随机变量（X）服从一个位置参数为 $\mu$ 、尺度参数为 $\sigma$ 的概率分布，其概率密度函数为

$\frac{1}{\sqrt {2\pi}\sigma} e^{-\frac{(x-\mu)^2}{2\sigma^2}}$

如果随机变量（X）服从一个数学期望为 $\mu$ ，方差为 $\sigma^2$ 的正态分布，记作 $X\sim N(\mu, \sigma^2)$ ，特别的，当 $\mu =0, \sigma^2 = 1$ 时，称为标准正态分布。

泊松分布

泊松分布是一种常见的离散型概率分布，刻画了单位时间内随机事件发生的次数，其概率密度函数为
$\frac{\lambda^k}{k!}e^{-\lambda}, k = 0, 1, 2,\cdots$

伯努利分布

伯努利分布常用来刻画0-1概率分布，如果随机变量（X）仅有两个可能的结果0和1，此时随机变量（X）取0和1两个值，相应的概率密度函数为
$\begin{cases} p, \quad X= 1\\ \\ 1-p,\quad X=0 \end{cases}$

两种绘制密度曲线的方法

某数据科学家通过算法模型获得一组预测值，其想要评估预测值与实际值之间偏差分布情况，可以绘制出偏差的概率分布函数曲线图或者直方图，观测这些偏差分布情况，这里给出两种绘制概率密度曲线的方法

matplotlib

matplotlib是python比较原生的绘图模块，适合平时使用习惯，功能强大用法友善，出场率高。

def density(column_1, column_2): #密度函数
    diff = abs(column_1 - column_2)  #差异率
    plt.figure(figsize = (6, 4)) #新建画布
    diff.plot(kind ='kde', label = u'观测值') #label = str(lower) +'~'+ str(upper)
    plt.grid(alpha = 0.5) #添加网格线
    plt.xlabel("偏差")
    plt.ylabel("密度值")
    plt.legend()
    plt.title("偏差密度分布图")
    plt.show()

预览效果

概率密度函数曲线及绘制
matplotlib绘制概率密度函数曲线主要调用了**kind =‘kde’**的参数，这是一种密度图（Kernel Density Estimate,核密度估计），它是通过模拟计算“可能会产生观测数据的连续情况概率分布的估计”而产生的，因此在调用plot时加上kind='kde’即可生成一张密度图，也就是我们看到的概率密度函数曲线图。

seaborn

seaborn也是python中的一个常用的可视化模块，是对matplotlib进行二次封装而成，所以有些方面要比matplotlib更简单更友好

def density(column_1, column_2): #密度函数
    diff = abs(column_1 - column_2)  #差异率
    plt.figure(figsize = (6, 4)) #新建画布
    sb.kdeplot(diff, label = 'density') #密度曲线
    plt.grid(alpha = 0.5) #添加网格线
    plt.xlabel("偏差")
    plt.ylabel("密度值")
    plt.legend()
    plt.title("偏差概率密度曲线")
    plt.show()

预览效果

概率密度函数曲线及绘制

seaborn就进一步把这个观测值连续模拟过程封装成了kdeplot函数，直接调用即可，但从两者的概率函数曲线来看，matplotlib更具有对称性，seaborn细节更丰富，我们可以从seaborn的密度函数曲线看到实际值的数量级和预测值的数量级大致在10000左右，偏差有大有小，但主要集中在-500到2000之间。

参考文献

1，https://baike.baidu.com/item/概率密度函数/5021996?fr=aladdin
2，https://zhuanlan.zhihu.com/p/48140593
3，https://www.zhihu.com/question/263467674
4，http://t.zoukankan.com/Renyi-Fan-p-13282258.html
5，https://blog.csdn.net/helloworld0906/article/details/103214392文章来源地址https://www.toymoban.com/news/detail-420367.html

到了这里，关于概率密度函数曲线及绘制的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！