(ICLR-2022)TADA！用于视频理解的时间自适应卷积

TADA！用于视频理解的时间自适应卷积

paper题目：TADA! TEMPORALLY-ADAPTIVE CONVOLUTIONS FOR VIDEO UNDERSTANDING

paper是NUS发表在ICLR 2022的工作

paper链接：地址

Code:地址

ABSTRACT

空间卷积广泛用于许多深度视频模型。它从根本上假设时空不变性，即对不同帧中的每个位置使用共享权重。这项工作提出了用于视频理解的时间自适应卷积 (TAdaConv)，这表明沿时间维度的自适应权重校准是促进视频中复杂时间动态建模的有效方法。具体来说，TAdaConv 通过根据其局部和全局时间上下文校准每帧的卷积权重，使空间卷积具有时间建模能力。与之前的时间建模操作相比，TAdaConv 更有效，因为它在卷积核而不是特征上进行操作，其维度比空间分辨率小一个数量级。此外，内核校准带来了模型容量的增加。我们通过用 TAdaConv 替换 ResNet 和 ConvNeXt 中的 2D 卷积来构建 TAda2D 和 TAdaConvNeXt 网络，与多个视频动作识别和定位基准上的最先进方法相比，这至少具有同等或更好的性能。我们还证明，作为一种计算开销可忽略不计的易于插入的操作，TAdaConv 可以有效地改进许多现有的视频模型，并具有令人信服的余量。

1 INTRODUCTION

卷积是现代深度视觉模型中不可或缺的操作（He et al., 2016; Szegedy et al., 2015; Krizhevsky et al., 2012），其不同的变体推动了卷积神经网络的最新性能网络（CNN）在许多视觉任务（Xie et al., 2017; Dai et al., 2017; Zhou et al., 2019）和应用场景（Howard et al., 2017; Y ang et al., 2019）中。在视频范例中，与 3D 卷积（Tran 等人，2015）相比，2D 空间卷积和 1D 时间卷积的组合由于其效率而受到更广泛的青睐（Tran 等人，2018；Qiu 等人， 2017）。尽管如此，一维时间卷积仍然在空间卷积之上引入了不可忽略的计算开销。因此，我们寻求直接为空间卷积配备时间建模能力。

卷积的一个基本属性是平移不变性 (Ruderman & Bialek, 1994; Simoncelli & Olshausen, 2001)，这是由于其局部连通性和共享权重。然而，最近的动态滤波器工作表明，对于各种空间内容的建模，所有像素的严格分片权重可能不是最优的（Zhou et al., 2021; Wu et al., 2018）。

鉴于视频中时间动态的多样性，我们假设时间建模也可以受益于沿时间维度的松弛不变性。这意味着不同时间步长的卷积权重不再严格共享。现有的动态滤波器网络可以实现这一点，但有两个缺点。首先，它们中的大多数（Zhou et al., 2021; Y ang et al., 2019）很难利用现有的预训练模型，例如 ResNet。这在视频应用中至关重要，因为从头开始训练视频模型对资源的要求很高（Feichtenhofer 等人，2019；Feichtenhofer，2020），并且容易在小型数据集上过度拟合。其次，对于大多数动态滤波器，权重是根据其空间上下文（Zhou et al., 2021; Jia et al., 2016）或全局描述符（Chen et al., 2020a; Y ang et al., 2019），难以捕捉帧之间的时间变化。

在这项工作中，我们提出了用于视频理解的时间自适应卷积（TAdaConv），其中卷积核权重不再在不同帧之间固定。具体来说，第$t$帧的卷积核${\mathbf{W}}_t$被分解为基础权重和校准权重的乘积：${\mathbf{W}}_t={\mathbf{\alpha }}_t\cdot {\mathbf{W}}_b$b，其中校准权重${\mathbf{\alpha }}_t$是从基础权重${\mathbf{W}}_b$中所有通道的输入数据中自适应生成的。对于每一帧，我们根据其相邻时间步长的帧描述符以及全局描述符生成校准权重，它有效地编码了视频中的局部和全局时间动态。 TAdaConv 和空间卷积之间的区别如图 1 所示。

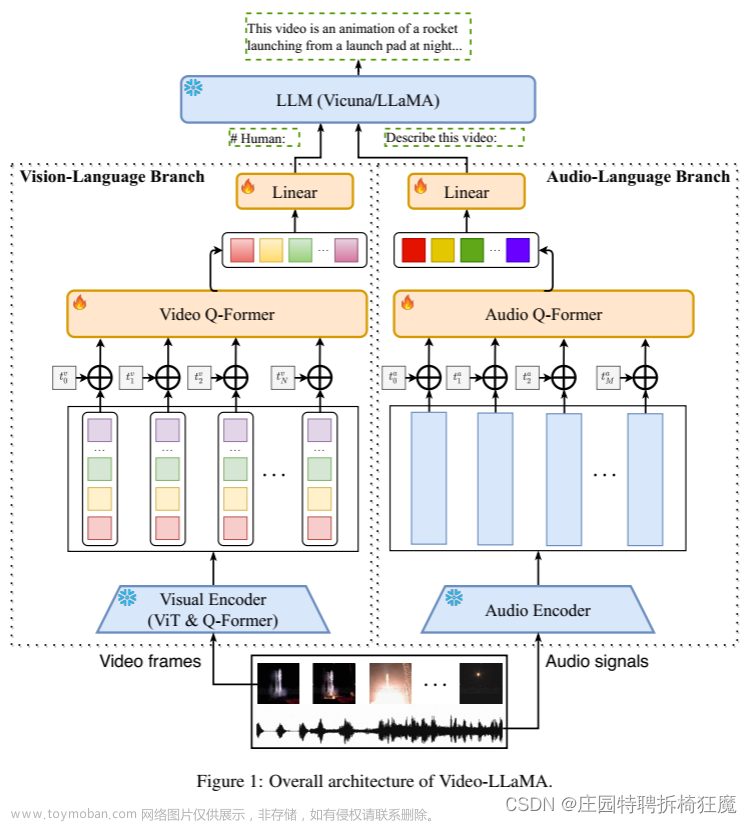
图1：TAdaConv和视频模型中的空间卷积的比较。(a) 视频中的标准空间卷积在不同帧之间共享内核权重。(b) 我们的TAdaConv通过时间上下文自适应地校准每一帧的内核权重。

这种分解的主要优点有三个方面：（i）TAdaConv可以很容易地插入到任何现有模型中，以增强时间建模，并且它们的预训练权重仍然可以利用；（ii）借助于时间自适应权重，可以极大地提高时间建模能力；（iii）与通常在学习的2D特征图上操作的时间卷积相比，TAdaConv通过直接操作卷积核更有效。

TAdaConv被提出作为现有模型中空间卷积的替代品。它既可以作为2D网络的独立时间建模模块，也可以插入到现有卷积视频模型中，以进一步增强建模时间动态的能力。为了提高效率，我们通过替换ResNet中的空间卷积来构建TAda2D（He等人，2016），这至少会导致与现有技术相当或更好的性能。作为现有视频模型的增强，TAdaConv对多个视频数据集进行了显著改进。强大的性能和持续的改进表明，TAdaConv可以成为视频中复杂时间动力学建模的重要操作。

2 RELATED WORK

时间建模的ConvNet。视频和图像的根本区别在于时间维度，这使得时间建模成为理解视频的重要研究领域。最近用于视频理解的深度CNN可分为两种类型。第一类通过三维卷积联合建模时空信息（Carreira和Zisserman，2017；Tran等人，2015；Feichtenhofer，2020；Tran等人，2019）。第二类基于2D网络，其中大多数方法采用2D卷积，在空间建模的所有帧之间共享权重，并为时间建模设计额外的操作，例如时间偏移（Lin等人，2019a）、时间差（Wang等人，2021；姜等人，2019），时间卷积（Tran等人，2018；Liu等人，2021b）和相关运算（Wang等人，2020）等。我们的工作直接使空间卷积具有时间建模能力，可以进一步与其他时间建模操作耦合，以获得更强的视频识别性能。

动态网络。动态网络是指具有内容自适应权重或模块的网络，例如动态滤波器/卷积（贾等人，2016；杨等人，2019；李等人，2021）、动态激活（李等人，2020d；陈等人，2020b）和动态路由（王等人，2018；李等人，2020c）等。与静态网络相比，动态网络已证明其超过了网络容量，因此具有更高的性能。在视频理解中，动态滤波器（Liu等人，2021b）或时间聚集（Meng等人，2021）也表现出强大的时间建模能力。最近，一些卷积应用了空间自适应权重（Elsayed等人，2020；Chen等人，2021），显示了在建模不同视觉内容时放松空间不变性的好处。同样，我们提出的TAdaConv通过松弛沿时间维度的不变性来增强时间建模。TAdaConv与以前的工作有两个关键区别：（i）将TAdaConv中的卷积权重分解为基准权重和校准权重，这使TAdaConv能够利用预训练的权重；（ii）根据时间上下文生成校准权重。

3 TADACONV: TEMPORALLY-ADAPTIVE CONVOLUTIONS

在这项工作中，我们试图使空间卷积具有时间建模能力。受时间卷积校准过程（第3.1节）的启发，TAdaConv根据其时间上下文（第3.2节）动态校准每个帧的卷积权重。

3.1 REVISITING TEMPORAL CONVOLUTIONS

我们首先重新审视时间卷积以展示其基本过程及其与动态过滤器的关系。为简单起见，我们考虑了深度时间卷积，由于其效率，它被更广泛地使用（Liu 等人，2021b；Jiang 等人，2019）。公式上，对于由$\mathbf{\beta }=\left[{\mathbf{\beta }}_1,{\mathbf{\beta }}_2,{\mathbf{\beta }}_3\right]$参数化并放置（忽略归一化）由$\mathbf{W}$参数化的 2D 卷积之后的$3\times 1\times 1$时间卷积滤波器，第$t$帧的输出特征${\tilde{\mathbf{x}}}_t$可以是通过以下方式获得：
$${\tilde{\mathbf{x}}}_t={\mathbf{\beta }}_1\cdot \delta \left(\mathbf{W}\ast {\mathbf{x}}_{t-1}\right)+{\mathbf{\beta }}_2\cdot \delta \left(\mathbf{W}\ast {\mathbf{x}}_t\right)+{\mathbf{\beta }}_3\cdot \delta \left(\mathbf{W}\ast {\mathbf{x}}_{t+1}\right),$$
其中$\cdot$表示逐元素乘法，$\ast$表示空间维度上的卷积，$\delta$表示 ReLU 激活 (Nair & Hinton, 2010)。可以改写如下：
$${\tilde{\mathbf{x}}}_t={\mathbf{W}}_{t-1}\ast {\mathbf{x}}_{t-1}+{\mathbf{W}}_t\ast {\mathbf{x}}_t+{\mathbf{W}}_{t+1}\ast {\mathbf{x}}_{t+1},$$
其中${\mathbf{W}}_{t-1}^{i,j}={\mathbf{M}}_{t-1}^{i,j}\cdot {\mathbf{\beta }}_1\cdot \mathbf{W},{\mathbf{W}}_t^{i,j}={\mathbf{M}}_t^{i,j}\cdot {\mathbf{\beta }}_2\cdot \mathbf{W}$和${\mathbf{W}}_{t+1}^{i,j}={\mathbf{M}}_{t+1}^{i,j}\cdot {\mathbf{\beta }}_3\cdot \mathbf{W}$是时空位置自适应卷积权重。${\mathbf{M}}_t\in {\mathbb{R}}^{C\times H\times W}$是一个动态张量，其值取决于空间卷积的结果。因此，(2+1)D 卷积中的时间卷积本质上执行 (i) 对空间卷积的权重校准和 (ii) 相邻帧之间的特征聚合。但是，如果通过将时间卷积与空间卷积耦合来实现时间建模，则仍然会引入不可忽略的计算开销（参见表 2）。

3.2 FORMULATION OF TADACONV

为了提高效率，我们着手直接赋予空间卷积时间建模能力。受最近发现空间不变性的松弛加强了空间建模的启发（Zhou 等人，2021；Elsayed 等人，2020），我们假设时间自适应权重也可以帮助时间建模。因此，TAdaConv 层中的卷积权重逐帧变化。由于我们观察到以前的动态过滤器几乎不能利用预训练的权重，我们从我们在时间卷积中的观察中获得灵感，并将第$t$帧${\mathbf{W}}_t$的权重分解为所有帧共享的基本权重${\mathbf{W}}_b$的乘积，以及每个时间步不同的校准权重${\mathbf{\alpha }}_t$：
$${\tilde{\mathbf{x}}}_t={\mathbf{W}}_t\ast {\mathbf{x}}_t=\left({\mathbf{\alpha }}_t\cdot {\mathbf{W}}_b\right)\ast {\mathbf{x}}_t,$$
校准权重生成。为了允许 TAdaConv 对时间动态进行建模，至关重要的是，第$t$帧的校准权重${\mathbf{\alpha }}_t$不仅要考虑当前帧，而且更重要的是，它的时间上下文，即${\mathbf{\alpha }}_t=\mathcal{G}\left(\dots ,{\mathbf{x}}_{t-1},{\mathbf{x}}_t,{\mathbf{x}}_{t+1},\dots \right)$。否则 TAdaConv 将退化为一组不相关的空间卷积，在不同的帧上应用不同的权重。我们在图 2（b）中展示了生成函数$\mathcal{G}$的实例化。

图 2：TAdaConv 的实例化和 TAda2D 中使用的时间特征聚合。(a) 视频模型中使用的标准卷积。 (b) 我们的 TAdaConv 使用具有全局时间上下文的非线性权重校准。 © TAda2D 中使用的时间特征聚合方案。

在我们的设计中，我们的目标是提高效率和捕捉帧间时间动态的能力。为了提高效率，我们对帧描述向量$\mathbf{v}\in {\mathbb{R}}^{T\times C}$进行操作，该向量是通过对每个帧的空间维度 GAP 进行全局平均池化获得的，即${\mathbf{v}}_t={\mathrm{GAP}}_s\left({\mathbf{x}}_t\right)$。对于时间建模，我们对从 x t a d j = { x t − 1 , x t , x t + 1 } \mathbf{x}_{t}^{a d j}=\left\{\mathbf{x}_{t-1}, \mathbf{x}_{t}, \mathbf{x}_{t+1}\right\} xtadj​={xt−1​,xt​,xt+1​}得到的局部时间上下文 v t a d j = { v t − 1 , v t , v t + 1 } \mathbf{v}_{t}^{a d j}=\left\{\mathbf{v}_{t-1}, \mathbf{v}_{t}, \mathbf{v}_{t+1}\right\} vtadj​={vt−1​,vt​,vt+1​}应用堆叠的两层一维卷积$\mathcal{F}$，降维率为$r$。
$$\mathcal{F}\left({\mathbf{x}}_t^{adj}\right)=Conv1D{\mathrm{D}}^{C/r\to C}\left(\delta \left(\mathrm{BN}\left(\mathrm{Conv}1{\mathrm{D}}^{C\to C/r}\left({\mathbf{v}}_t^{adj}\right)\right)\right)\right).$$
其中$\delta$和BN表示ReLU（Nair & Hinton，2010）和 batchnorm（Ioffe & Szegedy，2015）。

为了在局部一维卷积的基础上获得更大的帧间视野，我们通过线性映射函数FC将全局描述符$\mathrm{g}$添加到权重生成过程$\mathcal{F}$中，进一步纳入全局时间信息。
$$\mathcal{F}\left({\mathbf{x}}_t^{adj},\mathbf{g}\right)=\mathrm{Conv}1{\mathrm{D}}^{C/r\to C}(\delta \left(\mathrm{BN}\left(\mathrm{Conv}1{\mathrm{D}}^{C\to C/r}\left({\mathbf{v}}_t^{adj}+{\mathrm{FC}}^{C\to C}(\mathbf{g})\right)\right)\right),$$
其中$\mathrm{g}={\mathrm{GAP}}_{st}(\mathbf{x})$，${\mathrm{GAP}}_{st}$是空间和时间维度上的全局平均池化。

初始化。 TAdaConv 旨在通过简单地替换 2D 卷积轻松插入到现有模型中。为了有效使用预训练的权重，TAdaConv 被初始化为与标准卷积完全相同。这是通过将$\mathcal{F}$中最后一个卷积的权重初始化为零并向公式添加一个常数向量 1 来实现的：
$${\mathbf{\alpha }}_t=\mathcal{G}(\mathbf{x})=1+\mathcal{F}\left({\mathbf{x}}_t^{adj},\mathbf{g}\right).$$
这样，在初始状态，${\mathbf{W}}_t=1\cdot {\mathbf{W}}_b={\mathbf{W}}_b$，我们用预训练的权重加载${\mathbf{W}}_b$。

校准尺寸。基础权重${\mathbf{W}}_b\in {\mathbb{R}}^{C_{\text{out }}\times C_{\text{in }}\times k^2}$可以在不同维度上进行校准。我们在$C_{in}$维度$\left({\alpha }_t\in {\mathbb{R}}^{1\times C_{in}\times 1}\right)$上实例化校准，因为基于输入特征的权重生成比输出通道或空间结构更精确地估计输入通道的关系（经验分析表 7)。

与其他动态过滤器的比较。表 1 将 TAdaConv 与现有的动态过滤器进行了比较。基于专家混合的动态过滤器（例如 CondConv）动态聚合多个内核以生成所有位置共享的权重。大多数其他动态过滤器中的权重完全由输入生成，例如图像中的 DynamicFilter (Jia et al., 2016) 和 DDF (Zhou et al., 2021) 以及视频中的 TAM (Liu et al., 2021b)。与基于图像的相比，TAdaConv 通过从局部和全局时间上下文生成权重来实现时间建模。与 TANet (Liu et al., 2021b) 相比，TAdaConv 由于时间自适应权重而更擅长时间建模。此外，TAdaConv 可以有效地生成与预训练模型相同的权重，而以前的方法很难利用预训练模型。

表 1：与其他动态滤波器的比较。

与时间卷积的比较。表 2 比较了 TAdaConv 与 R(2+1)D 在参数和 FLOPs 中的比较，这表明我们在空间卷积之上的大部分额外计算开销比时间卷积小一个数量级。

表2：$(2+1)\mathrm{D}$卷积和TAdaConv在FLOPs和参数数上的比较。操作实例设置：$C_o=C_i=64,k=3,T=8,H=W=56$和$r=4$。网络设置示例。ResNet-50，输入分辨率为$8\times 224^2$。有色数字表示添加到二维卷积或ResNet-50的额外FLOPs/Params。

4 TADA2D: TEMPORALLY ADAPTIVE 2D NETWORKS

我们通过用我们提出的 TAdaConv 替换 ResNet（R2D）中的 2D 卷积来构建 TAda2D 网络。此外，基于跨步平均池化，我们提出了一个用于 2D 网络的时间特征聚合模块，对应于时间卷积的第二个基本步骤。如图2（c）所示，聚合模块放置在TAdaConv之后。公式上，给定 TAdaConv$\tilde{\mathbf{x}}$的输出，聚合特征可以得到如下：
$${\mathbf{x}}_{aggr}=\delta \left({\mathrm{BN}}_1(\tilde{\mathbf{x}})+{\mathrm{BN}}_2\left({\mathrm{TempAvgPool}}_k(\tilde{\mathbf{x}})\right)\right),$$
其中TempAvgPool${}_k$表示内核大小为$k$的跨步时间平均池化。我们对由TAdaConv$\tilde{\mathbf{x}}$提取并通过跨步平均池化TempAvgPool${\mathrm{Te}}_k(\tilde{\mathbf{x}})$聚合的特征使用不同的批量归一化参数，因为它们的分布本质上是不同的。在初始化过程中，我们将预训练的权重加载到 BN1，并将 BN2 的参数初始化为零。再加上 TAdaConv 的初始化，TAda2D 的初始状态与 Temporal Segment Networks 完全相同（Wang et al., 2016），而校准和聚合显着增加了模型的训练容量。在实验中，我们将此结构称为快捷（Sc.）分支和单独的 BN（SepBN.）分支。

参考文献

文章来源地址https://www.toymoban.com/news/detail-420467.html

到了这里，关于(ICLR-2022)TADA！用于视频理解的时间自适应卷积的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！