基于RL(Q-Learning)的迷宫寻路算法-Toy模板网

这篇具有很好参考价值的文章主要介绍了基于RL(Q-Learning)的迷宫寻路算法。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

强化学习是一种机器学习方法，旨在通过智能体在与环境交互的过程中不断优化其行动策略来实现特定目标。与其他机器学习方法不同，强化学习涉及到智能体对环境的观测、选择行动并接收奖励或惩罚。因此，强化学习适用于那些需要自主决策的复杂问题，比如游戏、机器人控制、自动驾驶等。强化学习可以分为基于价值的方法和基于策略的方法。基于价值的方法关注于寻找最优的行动价值函数，而基于策略的方法则直接寻找最优的策略。强化学习在近年来取得了很多突破，比如 AlphaGo 在围棋中战胜世界冠军。

强化学习的重要概念：

环境：其主体被嵌入并能够感知和行动的外部系统
主体：动作的行使者
状态：主体的处境
动作：主体执行的动作
奖励：衡量主体动作成功与否的反馈

问题描述

给定一个N*N矩阵，其中仅有-1、0、1组成该矩阵，-1表示障碍，0表示路，1表示终点和起点：

# 生成迷宫图像
def generate_maze(size):
    maze = np.zeros((size, size))
    # Start and end points
    start = (random.randint(0, size-1), 0)
    end = (random.randint(0, size-1), size-1)
    maze[start] = 1
    maze[end] = 1
    # Generate maze walls
    for i in range(size*size):
        x, y = random.randint(0, size-1), random.randint(0, size-1)
        if (x, y) == start or (x, y) == end:
            continue
        if random.random() < 0.2:
            maze[x, y] = -1
        if np.sum(np.abs(maze)) == size*size - 2:
            break
    return maze, start, end

上述函数返回一个numpy数组类型的迷宫，起点和终点

生成迷宫图像：

基于RL(Q-Learning)的迷宫寻路算法

使用BFS进行寻路：

# BFS求出路径
def solve_maze(maze, start, end):
    size = maze.shape[0]
    visited = np.zeros((size, size))
    solve = np.zeros((size,size))
    queue = [start]
    visited[start[0],start[1]] = 1
    while queue:
        x, y = queue.pop(0)
        if (x, y) == end:
            break
        for dx, dy in [(0, 1), (0, -1), (1, 0), (-1, 0)]:
            nx, ny = x + dx, y + dy
            if nx < 0 or nx >= size or ny < 0 or ny >= size or visited[nx, ny] or maze[nx, ny] == -1:
                continue
            queue.append((nx, ny))
            visited[nx, ny] = visited[x, y] + 1
    if visited[end[0],end[1]] == 0:
        return solve,[]
    path = [end]
    x, y = end
    while (x, y) != start:
        for dx, dy in [(0, 1), (0, -1), (1, 0), (-1, 0)]:
            nx, ny = x + dx, y + dy
            if nx < 0 or nx >= size or ny < 0 or ny >= size or visited[nx, ny] != visited[x, y] - 1:
                continue
            path.append((nx, ny))
            x, y = nx, ny
            break

    points = path[::-1]  # 倒序
    for point in points:
        solve[point[0]][point[1]] = 1
    return solve, points

上述函数返回一个numpy数组，和点组成的路径，图像如下：

基于RL(Q-Learning)的迷宫寻路算法

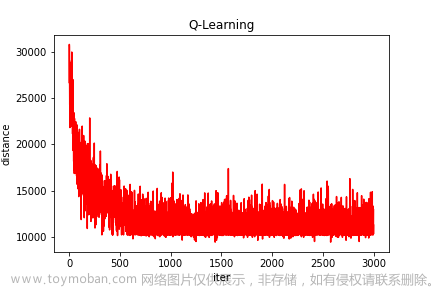
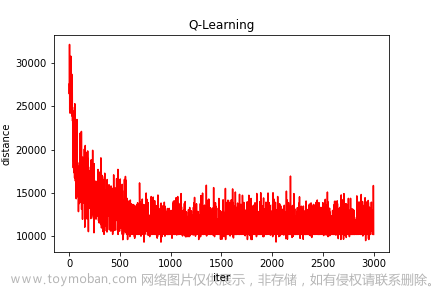
BFS获得的解毫无疑问是最优解，现在使用强化学习的方法来解决该问题(QLearning、DQN)

QLearning

该算法核心原理是Q-Table，其行和列表示State和Action的值，Q-Table的值Q(s,a)是衡量当前States采取行动a的重要依据

具体步骤如下：

初始化Q表
执行以下循环：
1. 初始化一个Q表格，Q表格的行表示状态，列表示动作，Q值表示某个状态下采取某个动作的价值估计。初始时，Q值可以设置为0或随机值。
2. 针对每个时刻，根据当前状态s，选择一个动作a。可以根据当前状态的Q值和某种策略（如贪心策略）来选择动作。
3. 执行选择的动作a，得到下一个状态s'和相应的奖励r$
4. 基于下一个状态s'，更新Q值。Q值的更新方式为：
  1. 初始化一个状态s。
  2. 根据当前状态s和Q表中的Q值，选择一个动作a。可以通过epsilon-greedy策略来进行选择，即有一定的概率随机选择动作，以便于探索新的状态，否则就选择Q值最大的动作。
  3. 执行选择的动作a，得到下一个状态s'和奖励r。
  4. 根据s'和Q表中的Q值，计算出最大Q值maxQ。
  5. 根据Q-learning的更新公式，更新Q值：Q(s, a) = Q(s, a) + alpha * (r + gamma * maxQ - Q(s, a))，其中alpha是学习率，gamma是折扣因子。
  6. 将当前状态更新为下一个状态：s = s'。
  7. 如果当前状态为终止状态，则转到步骤1；否则转到步骤2。
  8. 重复执行步骤1-7直到收敛，即Q值不再发生变化或者达到预定的最大迭代次数。最终得到的Q表中的Q值就是最优的策略。
5. 重复执行2-4步骤，直到到达终止状态，或者达到预设的最大步数。
6. 不断执行1-5步骤，直到Q值收敛。
7. 在Q表格中根据最大Q值，选择一个最优的策略。

代码实现

实现QLearningAgent类：

class QLearningAgent:
    def __init__(self,actions,size):
        self.actions = actions
        self.learning_rate = 0.01
        self.discount_factor = 0.9
        self.epsilon = 0.1  # 贪婪策略取值
        self.num_actions = len(actions)

        # 初始化Q-Table
        self.q_table = np.zeros((size,size,self.num_actions))

    def learn(self,state,action,reward,next_state):
        current_q = self.q_table[state][action]  # 从Q-Table中获取当前Q值
        new_q = reward + self.discount_factor * max(self.q_table[next_state])  # 计算新Q值
        self.q_table[state][action] += self.learning_rate * (new_q - current_q) # 更新Q表

    # 获取动作
    def get_action(self,state):
        if np.random.rand() < self.epsilon:
            action = np.random.choice(self.actions)
        else:
            state_action = self.q_table[state]
            action = self.argmax(state_action)
        return action

    @staticmethod
    def argmax(state_action):
        max_index_list = []
        max_value = state_action[0]
        for index,value in enumerate(state_action):
            if value > max_value:
                max_index_list.clear()
                max_value = value
                max_index_list.append(index)
            elif value == max_value:
                max_index_list.append(index)
        return random.choice(max_index_list)

类的初始化：

def __init__(self,actions,size):
    self.actions = actions
    self.learning_rate = 0.01
    self.discount_factor = 0.9
    self.epsilon = 0.1  # 贪婪策略取值
    self.num_actions = len(actions)

    # 初始化Q-Table
    self.q_table = np.zeros((size,size,self.num_actions))

上述代码中，先初始化动作空间，设置学习率，discount_factor是折扣因子，epsilon是贪婪策略去值，num_actions是动作数

def learn(self,state,action,reward,next_state):
    current_q = self.q_table[state][action]  # 从Q-Table中获取当前Q值
    new_q = reward + self.discount_factor * max(self.q_table[next_state])  # 计算新Q值
    self.q_table[state][action] += self.learning_rate * (new_q - current_q) # 更新Q表

该方法是QLearning的核心流程，给定当前状态、动作、赏罚和下一状态更新Q表

# 获取动作
def get_action(self,state):
    if np.random.rand() < self.epsilon:
        # 贪婪策略 随机选取动作
        action = np.random.choice(self.actions)
    else:
        # 从Q-Table中选择
        state_action = self.q_table[state]
        action = self.argmax(state_action)
    return action

该方法首先使用贪婪策略来决定是随机选择一个动作，还是选择 Q-Table 中当前状态对应的最大 Q 值对应的动作

@staticmethod
def argmax(state_action):
    max_index_list = []
    max_value = state_action[0]
    for index,value in enumerate(state_action):
        if value > max_value:
            max_index_list.clear()
            max_value = value
            max_index_list.append(index)
        elif value == max_value:
            max_index_list.append(index)
    return random.choice(max_index_list)

该方法首先获取最大值对应的动作，遍历Q表中的所有动作，找到最大值所对应的所有动作，最后从这些动作中随机选择一个作为最终的动作。

定义环境

下述定义了一个迷宫环境：

class MazeEnv:
    def __init__(self,size):
        self.size = size
        self.actions = [0,1,2,3]
        self.maze,self.start,self.end = self.generate(size)
	
    # 重置状态
    def reset(self):
        self.state = self.start
        self.goal = self.end
        self.path = [self.start]
        self.solve = np.zeros_like(self.maze)
        self.solve[self.start] = 1
        self.solve[self.end] = 1
        return self.state

    def step(self, action):
        # 执行动作
        next_state = None
        if action == 0 and self.state[0] > 0:
            next_state = (self.state[0]-1, self.state[1])
        elif action == 1 and self.state[0] < self.size-1:
            next_state = (self.state[0]+1, self.state[1])
        elif action == 2 and self.state[1] > 0:
            next_state = (self.state[0], self.state[1]-1)
        elif action == 3 and self.state[1] < self.size-1:
            next_state = (self.state[0], self.state[1]+1)
        else:
            next_state = self.state

        if next_state == self.goal:
            reward = 100
        elif self.maze[next_state] == -1:
            reward = -100
        else:
            reward = -1

        self.state = next_state  # 更新状态
        self.path.append(self.state)
        self.solve[self.state] = 1

        done = (self.state == self.goal)  # 判断是否结束

        return next_state, reward, done

    @staticmethod
    # 生成迷宫图像
    def generate(size):
        maze = np.zeros((size, size))
        # Start and end points
        start = (random.randint(0, size-1), 0)
        end = (random.randint(0, size-1), size-1)
        maze[start] = 1
        maze[end] = 1
        # Generate maze walls
        for i in range(size * size):
            x, y = random.randint(0, size-1), random.randint(0, size-1)
            if (x, y) == start or (x, y) == end:
                continue
            if random.random() < 0.2:
                maze[x, y] = -1
            if np.sum(np.abs(maze)) == size*size - 2:
                break
        return maze, start, end

    @staticmethod
    # BFS求出路径
    def solve_maze(maze, start, end):
        size = maze.shape[0]
        visited = np.zeros((size, size))
        solve = np.zeros((size,size))
        queue = [start]
        visited[start[0],start[1]] = 1
        while queue:
            x, y = queue.pop(0)
            if (x, y) == end:
                break
            for dx, dy in [(0, 1), (0, -1), (1, 0), (-1, 0)]:
                nx, ny = x + dx, y + dy
                if nx < 0 or nx >= size or ny < 0 or ny >= size or visited[nx, ny] or maze[nx, ny] == -1:
                    continue
                queue.append((nx, ny))
                visited[nx, ny] = visited[x, y] + 1
        if visited[end[0],end[1]] == 0:
            return solve,[]
        path = [end]
        x, y = end
        while (x, y) != start:
            for dx, dy in [(0, 1), (0, -1), (1, 0), (-1, 0)]:
                nx, ny = x + dx, y + dy
                if nx < 0 or nx >= size or ny < 0 or ny >= size or visited[nx, ny] != visited[x, y] - 1:
                    continue
                path.append((nx, ny))
                x, y = nx, ny
                break

        points = path[::-1]  # 倒序
        for point in points:
            solve[point[0]][point[1]] = 1
        return solve, points

执行

下面生成一个32*32的迷宫，并进行30000次迭代

maze_size = 32

# 创建迷宫环境
env = MazeEnv(maze_size)

# 初始化QLearning智能体
agent = QLearningAgent(actions=env.actions,size=maze_size)

# 进行30000次游戏
for episode in range(30000):
    state = env.reset()
    while True:
        action = agent.get_action(state)
        next_state,reward,done = env.step(action)
        agent.learn(state,action,reward,next_state)
        state = next_state
        if done:
            break
print(agent.q_table)  # 输出Q-Table

定义一个函数，用于显示迷宫的路线：

from PIL import Image

def maze_to_image(maze, path):
    size = maze.shape[0]
    img = Image.new('RGB', (size, size), (255, 255, 255))
    pixels = img.load()
    for i in range(size):
        for j in range(size):
            if maze[i, j] == -1:
                pixels[j, i] = (0, 0, 0)
            elif maze[i, j] == 1:
                pixels[j, i] = (0, 255, 0)
    for x, y in path:
        pixels[y, x] = (255, 0, 0)
    return np.array(img)

接下来显示三个图像：迷宫图像、BFS求解的路线、QLearning求解路线：

plt.figure(figsize=(16, 10))

image1 = maze_to_image(env.maze,[])
plt.subplot(1,3,1)
plt.imshow(image1)
plt.title('original maze')

_,path = env.solve_maze(env.maze,env.start,env.end)
image2 = maze_to_image(env.maze,path)
plt.subplot(1,3,2)
plt.imshow(image2)
plt.title('BFS solution')

image3 = maze_to_image(env.maze,env.path)
plt.subplot(1,3,3)
plt.imshow(image3)
plt.title('QL solution')

# 显示图像
plt.show()

显示：
基于RL(Q-Learning)的迷宫寻路算法文章来源地址https://www.toymoban.com/news/detail-420574.html