【Matlab】最小二乘法拟合多项式-Toy模板网

这篇具有很好参考价值的文章主要介绍了【Matlab】最小二乘法拟合多项式。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

前言

在最近的电机项目中，有遇到有传感器数据并不线性的问题，然后想要用最小二乘法做个曲线拟合，反过来去校准不线性的传感器的数据，因此记录一下使用最小二乘法来拟合多项式的曲线的步骤。本篇从最小二乘法的原始公式入手编写M文件，目的是方便使用单片机实现，或者说是方便用C来实现。

拟合一次函数：

我们先试着拟合一个简单一点的，从一元一次函数开始。最小二乘法拟合曲线需要首先知道曲线的通用公式。一次函数的通用公式为y = k * x + b，使用matlab编写很容易实现。这里我直接写入了几个点，随便编了一组数据。

【Matlab】最小二乘法拟合多项式

%*************************************************************************%
                %最小二乘法
%**********************************************************************%

clc;
clear;

%假定拟合曲线的公式为：y = ax^2 +b^x + c;
x = [1 2 3 4 5 6 7 8 9];
y = [1.2  2.5  3.6  4.8  5.6  7.4  8.0  9.8  12.0];
[m , n] = size(x);
sumx = 0;
sumy = 0;
sumxx = 0;
sumxy = 0;
Xaver = 0;
Yaver = 0;
XYaver = 0;
XXaver = 0;

%求平均
for i = 1 : n
    sumx = sumx + x(i);
    sumy = sumy + y(i);
    sumxy = sumxy + x(i) * y(i);
    sumxx = sumxx + x(i) * x(i);
end
Xaver = sumx / n;
Yaver = sumy / n;
XYaver = sumxy / n;
XXaver = sumxx / n;

k = (XYaver - Xaver * Yaver) / (XXaver - Xaver * Xaver);
b = Yaver - k * Xaver;

plot(x,y,'s');   %画数据点不连线
hold on;  %不加此句，两个图形将显示在两张图像上

%画出拟合曲线
x1 = [0 : 0.1 : 10];
y1 = k * x1 + b;

plot(x1,y1);

效果：

【Matlab】最小二乘法拟合多项式

拟合二次函数：

之后开始拟合二次函数，可以从最小二乘法的原理上进行程序编写。

最小二乘法原理：

假设我们的多项式表达式为：

【Matlab】最小二乘法拟合多项式

之后采集x与y的样本数据：

x = [1 2 3 4 5 6 7 8 9 10 11 12 13];
y = [1.2  2.5  3.6  4.8  5.6  6.6  7.4  8.0  9.8  12.0  12.5 13.1 14.6];

最小二乘法是要达到最优函数的各项系数使的误差平方和S取得最小值，即S对各项式的偏导为0：

【Matlab】最小二乘法拟合多项式

整理上式可得：

【Matlab】最小二乘法拟合多项式

将其转化为矩阵形式：

【Matlab】最小二乘法拟合多项式

即，我们需要求取样本x的和，x^2的和，，，，，x^n的加和，以及y的加和，xy的加和。。。。。x^n*y的加和。

假定我们的曲线是二次多项式，那么这个XY矩阵都是一个3行3列的矩阵，那么只需要求到x^4的加和即可，程序如下：

sumx = 0;
sumxx = 0;
sumxxx = 0;
sumxxxx = 0;
sumy = 0;
sumxy = 0;
sumxxy = 0;

%求矩阵数据
for i = 1 : n
    sumx = sumx + x(i);
    sumxx = sumxx + x(i) * x(i);
    sumxxx = sumxxx + x(i) * x(i) * x(i);
    sumxxxx = sumxxxx + x(i) * x(i) * x(i) * x(i);
    sumy = sumy + y(i);
    sumxy = sumxy + x(i) * y(i);
    sumxxy = sumxxy + x(i) * x(i) * y(i);
end

将x加和的相关项写成X矩阵，将y加和的相关项写成Y矩阵，之后：

【Matlab】最小二乘法拟合多项式

多项式矩阵就可以通过X矩阵的逆 * Y矩阵求得：

%写出矩阵
U = [n  sumx  sumxx ; sumx  sumxx  sumxxx ; sumxx  sumxxx  sumxxxx];
W = [sumy ; sumxy ; sumxxy];

%求出矩阵的逆，进而求出多项式矩阵
V =  pinv(U) * W;   % U * V = W    V = U(-1) * W
a = V(1,1); b = V(2,1); c = V(3,1);

之后就可以画出图形：

%画出拟合曲线
x1 = [0 : 0.1 : 15];
y1 = a + b .* x1 + c .* x1 .* x1;

plot(x1,y1);

注意：有一个点乘

结果图像如下:

【Matlab】最小二乘法拟合多项式

完整代码如下：

%*************************************************************************%
                %最小二乘法拟合多项式
%**********************************************************************%

clc;
clear;

%假定拟合曲线的公式为：y = a +b^x + c * x^2;
x = [1 2 3 4 5 6 7 8 9 10 11 12 13];
y = [1.2  2.5  3.6  4.8  5.6  6.6  7.4  8.0  9.8  12.0  12.5 13.1 14.6];
[m , n] = size(x);
a = 0;
b = 0;
c = 0;
sumx = 0;
sumxx = 0;
sumxxx = 0;
sumxxxx = 0;
sumy = 0;
sumxy = 0;
sumxxy = 0;

%求矩阵数据
for i = 1 : n
    sumx = sumx + x(i);
    sumxx = sumxx + x(i) * x(i);
    sumxxx = sumxxx + x(i) * x(i) * x(i);
    sumxxxx = sumxxxx + x(i) * x(i) * x(i) * x(i);
    sumy = sumy + y(i);
    sumxy = sumxy + x(i) * y(i);
    sumxxy = sumxxy + x(i) * x(i) * y(i);
end


%写出矩阵
U = [n  sumx  sumxx ; sumx  sumxx  sumxxx ; sumxx  sumxxx  sumxxxx];
W = [sumy ; sumxy ; sumxxy];

%求出矩阵的逆，进而求出多项式矩阵
V =  pinv(U) * W;   % U * V = W    V = U(-1) * W
a = V(1,1); b = V(2,1); c = V(3,1);

plot(x,y,'s');   %画数据点不连线
hold on;  %不加此句，两个图形将显示在两张图像上

%画出拟合曲线
x1 = [0 : 0.1 : 15];
y1 = a + b .* x1 + c .* x1 .* x1;

plot(x1,y1);

拟合多项式：

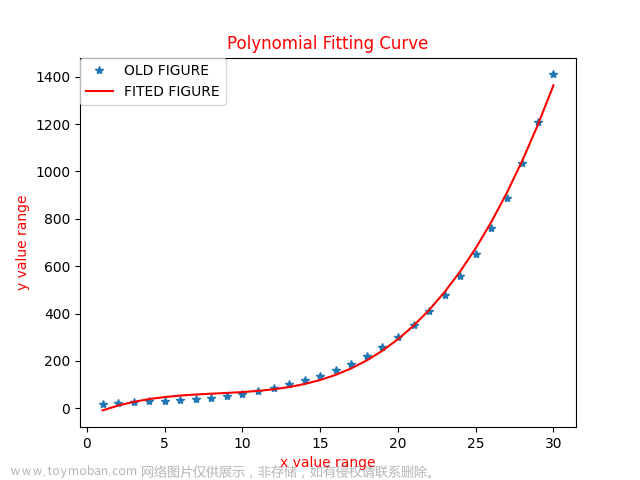
拟合多项式其实与拟合二次函数的方法是一样的，因为都是通用的矩阵。那就用一个4阶的举例，如果是4阶，那么拟合出来的多项式就是3次多项式。这里我们先随便编一个4次多项式，生成一个4次多项式的点：

for i = 1 : n
    y(i) = 0.3 + 0.04 * x(i) + 1.2 * x(i) * x(i) + 0.06 * x(i) * x(i) * x(i) + 0.003 * x(i) * x(i) * x(i) * x(i);
end

这里的y就是4次多项式了，生成了点之后，我们使用最小二乘法来拟合一个3次多项式，尽量与4次多项式的点接近。依旧是按照最小二乘法的矩阵公式，先求出需要的加和数据：

%求矩阵数据
for i = 1 : n
    sumx = sumx + x(i);
    sumxx = sumxx + x(i) * x(i);
    sumxxx = sumxxx + x(i) * x(i) * x(i);
    sumxxxx = sumxxxx + x(i) * x(i) * x(i) * x(i);
    sumxxxxx = sumxxxxx + x(i) * x(i) * x(i) * x(i) * x(i);
    sumxxxxxx = sumxxxxxx + x(i) * x(i) * x(i) * x(i) * x(i) * x(i);
    sumy = sumy + y(i);
    sumxy = sumxy + x(i) * y(i);
    sumxxy = sumxxy + x(i) * x(i) * y(i);
    sumxxxy = sumxxxy + x(i) * x(i) * x(i) * y(i);
    sumxxxxy = sumxxxxy + x(i) * x(i) * x(i) * x(i) * y(i);   
end

然后写出矩阵：

%写出矩阵
U = [n  sumx  sumxx  sumxxx; 
    sumx  sumxx  sumxxx  sumxxxx; 
    sumxx  sumxxx  sumxxxx  sumxxxxx;
    sumxxx  sumxxxx  sumxxxxx  sumxxxxxx];
W = [sumy ; sumxy ; sumxxy; sumxxxy];

求出逆矩阵之后求多项式：

%求出矩阵的逆，进而求出多项式矩阵
V =  pinv(U) * W;   % U * V = W    V = U(-1) * W
a = V(1,1); b = V(2,1); c = V(3,1);d = V(4,1);

之后将图像画出来，对比之前生成的点的图像：

plot(x,y,'s');   %画数据点不连线
hold on;  %不加此句，两个图形将显示在两张图像上

%画出拟合曲线
x1 = [0 : 0.1 : 40];
y1 = a + b .* x1 + c .* x1 .* x1 + d .* x1 .* x1 .* x1;

plot(x1,y1);

【Matlab】最小二乘法拟合多项式文章来源地址https://www.toymoban.com/news/detail-420828.html