CRC校验码生成逻辑的实现原理详解——结合C语言和Verilog语言代码分析-Toy模板网

这篇具有很好参考价值的文章主要介绍了CRC校验码生成逻辑的实现原理详解——结合C语言和Verilog语言代码分析。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

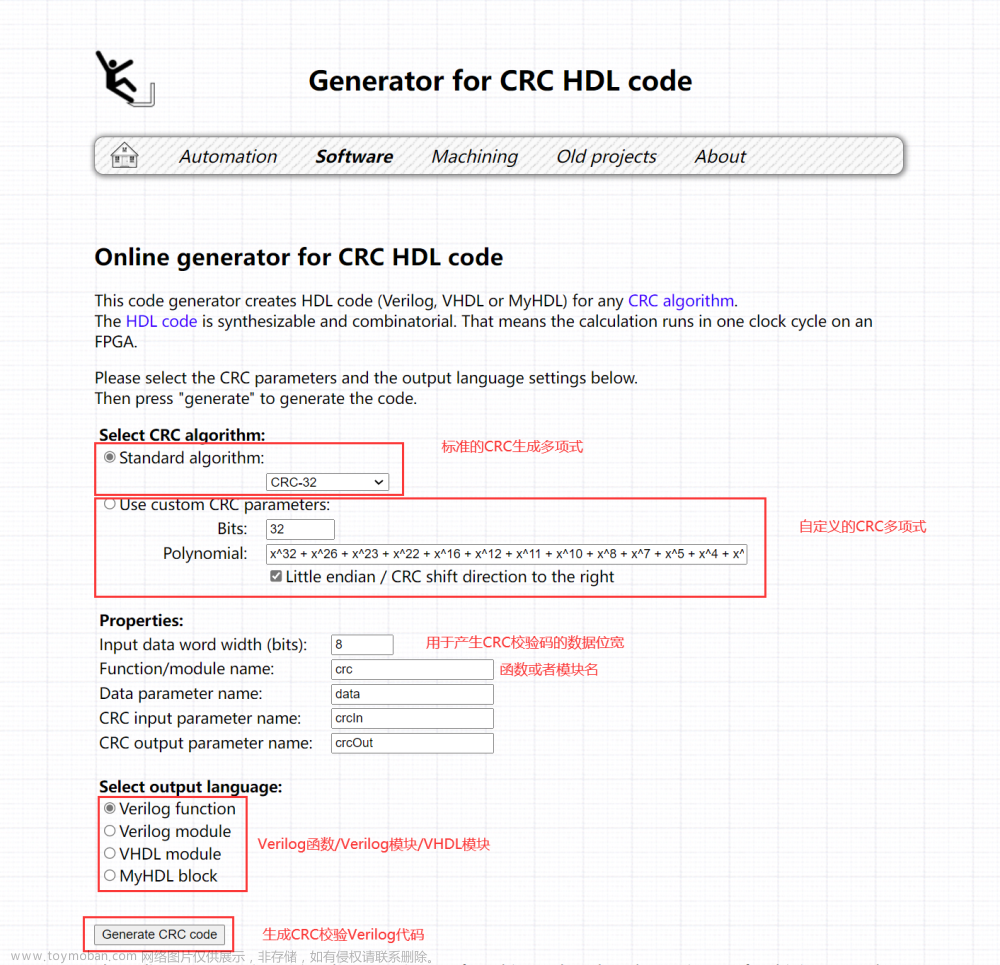
前言

因为前段时间用到CRC校验码，所以在网上找到了很多有关CRC校验码计算原理以及生成CRC校验码的代码实现（包括C语言和Verilog语言的实现）的文章，但关于CRC校验码代码实现的原理未能找到相关文章，于是自己结合C语言和Veirlog语言的实现代码以及CRC校验码的计算原理，对CRC校验码生成的实现原理进行分析。
本文基于读者对CRC及其运算已有了解，对于CRC及其运算可以参考文章《基于FPGA的CRC校验码生成器》，里面还有CRC的Verilog实现代码。

一、CRC校验码的计算

1.CRC模型

为了简化计算过程，本文采用以下的CRC校验码模型进行分析：

CRC参数	Value
`位宽`	`8`
`多项式`	`0x07`
`初始值`	`0x01`
结果异或值	0x00
输入数据反转	否
输出数据反转	否

结果异或值、输入数据反转、输出数据反转都是对数据在输入之前或者对经过了CRC核心生成逻辑输出的结果进行一些操作，而与CRC核心生成逻辑无关。所以对它们就不赘述了。值得一提的是，输入数据反转和输出数据反转的反转不是对数据进行按位取反，而是对数据进行倒序操作。
回归正题，基于上面表格里的CRC校验码模型（下称CRC模型1），下面我们来计算一个8位数据0xa8的校验码。

2.CRC计算

步骤1：输入数据与初始值模2加并左移

因为不需要对输入数据进行反转，所以我们第一步是要将输入数据和初始值进行模2加并左移8（位宽）位得到被除数（模2除）。

=======================
代码块1
=======================
10101000
00000001
--------
10101001 << 8 => 1010100100000000

步骤2：被除数与多项式模2除

因为多项式首位必然是1，所以我们在表达多项式的时候都是省略首位的1的，多项式0x07实际为0x107，我们第二步将步骤1得到的被除数与多项式进行模2除得到的余数即为CRC校验码，即数据0xa8在CRC模型1下的CRC校验码为0x56。

=======================
代码块2
=======================
		  			10101010	
		    ----------------				
  100000111|1010100100000000					
			100000111			(1)
			----------------				
			 010101010						
			 000000000			(2)
			----------------				
			  101010100						
			  100000111			(3)
			----------------				
			   010100110					
			   000000000		(4)
			----------------				
				101001100					
				100000111		(5)
			----------------				
				 010010110					
				 000000000		(6)
			----------------				
				  100101100					
				  100000111		(7)
			----------------				
				   001010110				
				   000000000	(8)
			----------------				
					01010110

二、CRC校验码生成逻辑的C语言实现

1.实现代码

基于CRC模型1，直接上C语言实现代码：

=======================
代码块3
=======================
#include <stdio.h>

unsigned char crc8_8bits_init0x01(unsigned char *data, unsigned int datalen){
	unsigned char crc_init = 0x01;
	unsigned char crc_poly = 0x07;
	
	while (datalen--){
		crc_init ^= *(data++);
		for(int i=0;i<8;i++){   
			if(crc_init & 0x80){
				crc_init = (crc_init << 1) ^ crc_poly;
            }
			else{
				crc_init = (crc_init << 1) ^ 0x00;
            }
		}
	}
	return (crc_init);
}

int main(){
    unsigned char data_in[1] = {0xa8};
    unsigned char crc_out = crc8_8bits_init0x01(data_in,sizeof(data_in));
    printf("crc_out = %#2x\n",crc_out);
    return 0;
}
=======================
运行结果：
crc_out = 0x56
=======================

2.代码分析

可以看到代码块3的C语言实现过程其实和代码块1和代码块2的实现过程一摸一样。

`代码块3`	`代码块1`	`代码块2`
`crc_init ^= *(data++)`	输入数据和初始值的模2加	/
for循环里的`crc_init << 1`	左移8位得到新数据	/
整个for循环	/	整个模2除过程即步骤(1) - (8)
for循环里的if判断语句	/	步骤(1) - (8)是跟poly还是跟0x00模2加

这是一个8位输入的CRC校验码生成函数，文章后面会讲到不同位宽输入的CRC校验码生成函数。

3.输入数据与初始值模2加的分析

初始值到底是什么？我们基于CRC模型1，但把初始值改为我们比较常用的0x00，得到一个新模型（下称CRC模型2），那很显然，这个时候我们的输入数据给0xa9，则会得到CRC模型1下输入数据给0xa8时一样的CRC8校验码0x56。
那假设对于CRC模型2，我们输入一个16位数据，即将这个16位数据拆分成两个8位的数据后先后输入到代码块3的8位输入的CRC校验码函数中（能拆分输入的原因将在下文讲述），并且我们让第一个8位数据输入以后得到的CRC8校验码为0x01，然后第二个数据给跟CRC模型1下一样的输入数据0xa8，则很显然最终也会得到CRC8校验码0x56。直接上代码来证明：

=======================
代码块4
=======================
#include <stdio.h>

unsigned char crc2datain_crc8(unsigned char crc_out){
	unsigned char crc_poly = 0x07;

	for(int i=0;i<8;i++){
		if(crc_out & 0x01){
			crc_out ^= crc_poly;
			crc_out = (crc_out >> 1) + 0x80;
		}
		else{
			crc_out = (crc_out >> 1) + 0x00;
		}
	}
	return(crc_out);
}

int main(){
    unsigned char data_in = crc2datain_crc8(0x1);
    printf("data_in = %#2x\n",data_in);
    return 0;
}
=======================
运行结果：
data_in= 0xd9
=======================

运行上面代码得到了我们要输入到CRC模型2的第一个8位数据是0xd9。
我们再将紧接在后面的的第二个8位输入数据给成在CRC模型1下给的输入数据0xa8，直接上代码：

=======================
代码块5
=======================
#include <stdio.h>

unsigned char crc8_8bits_init0x00(unsigned char *data, unsigned int datalen){
	unsigned char crc_init = 0x00;
	unsigned char crc_poly = 0x07;
	
	while (datalen--){
		crc_init ^= *(data++);
		for(int i = 0;i < 8;i++){   
			if(crc_init & 0x80){
				crc_init = (crc_init << 1) ^ crc_poly;
            }
			else{
				crc_init = (crc_init << 1) ^ 0x00;
            }
		}
	}
	return (crc_init);
}

int main(){
    unsigned char data_in[2] = {0xd9,0xa8};
    unsigned char crc_out = crc8_8bits_init0x00(data_in,sizeof(data_in));
    printf("crc_out = %#2x\n",crc_out);
    return 0;
}
=======================
运行结果：
crc_out = 0x56
=======================

最终得到的crc校验码确实一样都是0x56。
所以初始值其实是由前面的数据产生的CRC校验码，在这个基础上我们再将紧接在后面的输入数据与其模2加得到被除数再继续往下计算。
那么问题来了，我们为什么要将输入数据和初始值进行模2加，要探究这个问题就要回归校验码的本质了，这会在文章最后面进行简述，详情读者可自行查阅资料。下面我们先来探讨下Verilog语言写的CRC校验码生成器。

三、CRC校验码生成逻辑的Verilog语言实现

1.对应C语言8位输入CRC生成逻辑的Verilog语言实现

还是基于CRC模型1，对应C语言的8位输入CRC校验码生成函数，直接上Verilog语言实现代码：

=======================
代码块6
=======================
`timescale 1ns/1ns

module crc_gen#(
	parameter CRC_WIDTH 	= 8,
	parameter CRC_POLY  	= 7,
	parameter CRC_INIT  	= 1,
	parameter DATA_WIDTH  	= 8
	)(
	input							rst_n,
	input							clk,
	input							crc_en,
	input		[DATA_WIDTH-1:0] 	data_in,
	output reg	[CRC_WIDTH-1:0] 	crc_out
	);

	integer i;

	always @(posedge clk or negedge rst_n) begin
		if(!rst_n) begin
			crc_out = CRC_INIT;
		end
		else if(crc_en) begin
			crc_out = crc_out ^ data_in;
			for(i=0;i<DATA_WIDTH;i=i+1) begin
				if(crc_out[DATA_WIDTH-1] & 1'b1) begin
					crc_out = (crc_out << 1) ^ CRC_POLY;
				end
				else begin
					crc_out = (crc_out << 1);
				end
			end
		end
		else begin
			crc_out = crc_out;
		end
	end
endmodule

testbench代码如下：

=======================
代码块7
=======================
`timescale 1ns/1ns

module tb();
	localparam CRC_WIDTH 	= 8;
	localparam CRC_POLY		= 7;
	localparam CRC_INIT		= 1;
	localparam DATA_WIDTH 	= 8;

	reg 					rst_n;
	reg 					clk;
	reg 					crc_en;
	reg  [DATA_WIDTH-1:0]  	data_in;
	wire [CRC_WIDTH-1:0] 	crc_out;

	initial begin
		rst_n = 0;
		#10 rst_n = 1;
	end
	initial begin
		clk = 0;
		forever #5 clk = !clk;
	end
	initial begin
		crc_en = 1;
		#10 data_in = 8'ha8;
		forever #10 data_in = {$random} % 2**DATA_WIDTH;
	end
	crc_gen #(
		.CRC_WIDTH 	(CRC_WIDTH 	),
		.CRC_POLY  	(CRC_POLY  	),
		.CRC_INIT  	(CRC_INIT  	),
		.DATA_WIDTH (DATA_WIDTH )
	) crc_gen_u(
		.rst_n		(rst_n		),
		.clk		(clk		),
		.crc_en		(crc_en		),
		.data_in	(data_in	),
		.crc_out	(crc_out	)
	);
endmodule

仿真结果如下：
CRC校验码生成逻辑的实现原理详解——结合C语言和Verilog语言代码分析
可以看到跟C语言实现的结果是一致的，基于CRC模型1，输入数据为0xa8时，CRC校验码为0x56。
实现原理也是一致的：

Verilog语言（`代码块6`）	C语言（`代码块3`）
`crc_out = crc_out ^ data_in`	`crc_init ^= *(data++)`
for循环	for循环

2.基于LFSR模型的Verilog语言实现

还是基于CRC模型1，直接上基于LFSR模型的Verilog语言实现代码：

=======================
代码块8
=======================
`timescale 1ns/1ns

module crc_gen#(
	parameter CRC_WIDTH 	= 8,
	parameter CRC_POLY  	= 7,
	parameter CRC_INIT  	= 1,
	parameter DATA_WIDTH  	= 8
	)(
	input 							clk,
	input 							rst_n,
    input							crc_en,
    input		[DATA_WIDTH-1:0] 	data_in,
    output reg	[CRC_WIDTH-1:0] 	crc_out
);	

integer i;
reg fb_en;
always@( posedge clk or negedge rst_n) begin
	if(!rst_n) begin 
		crc_out = CRC_INIT;
	end
	else if(crc_en) begin
		for(i=DATA_WIDTH-1;i>=0;i=i-1) begin
			fb_en    	= crc_out[7] ^ data_in[i]	;
			crc_out[7]  = crc_out[6]				;
			crc_out[6]  = crc_out[5]				;
			crc_out[5]  = crc_out[4] 				;
			crc_out[4]  = crc_out[3]				;
			crc_out[3]  = crc_out[2]				;
			crc_out[2]  = crc_out[1] ^ fb_en 		;
			crc_out[1]  = crc_out[0] ^ fb_en 		;
			crc_out[0]  = fb_en						;
		 end	
	end
	else begin
		crc_out = crc_out;
	end
end
endmodule

进行仿真可以看到，仿真结果与第一种实现方法是一致的。
为了比较直观看到Verilog语言的CRC生成逻辑，以上的Verilog代码并没有将组合逻辑和时序逻辑分开写，将两种逻辑分开写自然是最好的。
更多关于基于LFSR模型实现的CRC校验码生成器和基于LFSR模型实现的伪随机码生成器可参考文章《基于FPGA的CRC校验码生成器》。

3.两种Verilog语言的CRC校验码生成逻辑的联系

基于LFSR模型的实现逻辑和对应C语言的8位输入CRC校验码生成函数的实现逻辑，两种逻辑既然能输出同样结果，说明两者必然存在着联系。

(1)基于LFSR模型的Verilog语言实现代码的逻辑等价变换

还是基于CRC模型1，下面我们先稍微对基于LFSR模型的Verilog语言实现代码即代码块8，进行一下逻辑等价变换：

=======================
代码块9
=======================
`timescale 1ns/1ns

module crc_gen#(
	parameter CRC_WIDTH 	= 8,
	parameter CRC_POLY  	= 7,
	parameter CRC_INIT  	= 1,
	parameter DATA_WIDTH  	= 8
	)(
	input 							clk,
	input 							rst_n,
    input							crc_en,
    input		[DATA_WIDTH-1:0] 	data_in,
    output reg	[CRC_WIDTH-1:0] 	crc_out
);	

integer i;
reg fb_en;
always@( posedge clk or negedge rst_n) begin
	if(!rst_n) begin 
		crc_out = CRC_INIT;
	end
	else if(crc_en) begin
		for(i=DATA_WIDTH-1;i>=0;i=i-1) begin
			fb_en    	= crc_out[7] ^ data_in[i];
			crc_out[7]  = crc_out[6] ^ (fb_en & CRC_POLY[7]);
			crc_out[6]  = crc_out[5] ^ (fb_en & CRC_POLY[6]);
			crc_out[5]  = crc_out[4] ^ (fb_en & CRC_POLY[5]);
			crc_out[4]  = crc_out[3] ^ (fb_en & CRC_POLY[4]);
			crc_out[3]  = crc_out[2] ^ (fb_en & CRC_POLY[3]);
			crc_out[2]  = crc_out[1] ^ (fb_en & CRC_POLY[2]);
			crc_out[1]  = crc_out[0] ^ (fb_en & CRC_POLY[1]);
			crc_out[0]  = 		   0 ^ (fb_en & CRC_POLY[0]);
		 end	
	end
	else begin
		crc_out = crc_out;
	end
end
endmodule

进行仿真可以看到，仿真结果与前面的一致。因为代码块9和代码块8的实现在逻辑上是等价的。

(2)对应变换后的Verilog代码的C语言代码

对应代码块9，直接上C语言代码：

=======================
代码块10
=======================
#include <stdio.h>

unsigned char crc8_1bit_init0x01(unsigned char *data, unsigned int datalen){
	unsigned char crc_init = 0x01;
	unsigned char crc_poly = 0x07;
	
	while (datalen--){
		crc_init ^= (*(data++) << 7);
		if(crc_init & 0x80){
			crc_init = (crc_init << 1) ^ crc_poly;
		}
		else{
			crc_init = (crc_init << 1) ^ 0x00;
		}
	}
	return (crc_init);
}
int main(){
    unsigned char data_in[8] = {1,0,1,0,1,0,0,0};
    unsigned char crc_out = crc8_1bit_init0x01(data_in,sizeof(data_in));
    printf("crc_out = %#2x\n",crc_out);
    return 0;
}
=======================
运行结果：
crc_out = 0x56
=======================

两者对应逻辑：

Verilog语言（`代码块9`）	C语言（`代码块10`）
for循环	while循环
`fb_en = crc_out[7] ^ data_in[i]`	`crc_init ^= (*(data++) << 7)`
`crc_out[i] = crc_out[i-1] ^ (fb_en & CRC_POLY[i])`	while循环里if判断语句块

(3)不同位宽输入数据的C语言实现代码

在前面我们说到当我们想要得到基于CRC模型2下的16位输入数据的校验码，我们可以将这个16位数据拆分位两个8位数据，然后将这两个8位数据先后输入到8位输入的CRC校验码生成函数中即可。
那么同理，当我们的输入数据为8位时，我们也可以将它拆分为8个1位数据，然后先后将这8个1位数据输入到1位输入的CRC校验码生成函数中即可。而这正好分别是我们的代码块3和代码块10里面的实现逻辑。那么我们为什么可以这样做呢？

①CRC校验码生成函数到底做了什么？

我们来看下CRC校验码生成函数到底做了什么，其实就是做了两件事：
事情①：将输入数据的每一位与初始值的相应位进行异或；
事情②：在循环里执行if判断语句块。
在代码块3的8位输入的CRC校验码生成函数里，我们在for循环外面就完成了事情①，然后在for循环里面完成事②，事情①和事情②的完成在时间上完全独立。
在代码块10的1位输入的CRC校验码生成函数里，我们在while循环里面，每一次循环完成事情①的一环再完成事情②的一环，在最后一次循环才完成了事情①紧接着完成事情②。
两个CRC校验码生成函数都完成了事情①和事情②，那么他们做的事情①和事情②是不是都是相同的，换言之，它们各自所做的事情①是不是对数据进行了同样的操作，各自所做的事情②是不是对数据进行了同样的操作。
对于事情①，代码块3在for循环外面的那个语句crc_init ^= *(data++)就是将输入数据的每一位与初始值的相应位进行异或。而代码块10，每一次循环，crc_init的最高位都与当次循环的那一位输入数据进行异或，然后crc_init左移1，也就是将crc_init的最高位变成了下一位，然后再在下一次循环里跟下一次的那一位数据进行异或……这样直到循环结束。所以它也是在循环里将输入数据的每一位与初始值的相应位进行了异或。即它们各自所做的事情①对数据进行了同样的操作。
对于事情②，代码块3和代码块10在循环里执行了相同次数的相同的if判断语句块，那么只要在每一次循环里，执行if判断语句里的判断条件crc_init & 0x80之前，确保crc_init & 0x80是一致的，即crc_init的最高位是一致的。很显然是一致的，因为在执行if判断语句里的判断条件crc_init & 0x80之前，它们都已经完成了事情①或者完成了事情①的那一环，将crc_init的最高位和当次循环的那一位输入数据进行了异或。所以它们各自所做的事情②对数据进行了同样的操作。
所以代码块3和代码块10里面的实现逻辑将会输出一样的结果。

②输入数据位宽超过CRC校验码位宽的CRC校验码生成函数

有了上面的分析，显而易见，将一个16位数据拆分为两个8位数据，然后将这两个8位数据先后输入到8位输入的CRC校验码生成函数，跟将一个16位数据输入到16位输入的CRC校验码生成函数，输出结果是一致的。
在8位输入的CRC校验码生成函数中，crc_init即CRC校验码是一直在左移的，一共左移了8次，那么当我们输入拆分的第一个数据后，CRC校验码左移了8次，那当我们输入拆分的第二个数据时，那它的每一位将与crc_init后面的8位的相应位进行异或。
那这对应到16位输入的CRC校验码生成函数，我们需要将16位输入数据与crc_init连同后面加的8个相应位进行异或，那为了不影响前后操作的结果，这后面加的8个相应位里面的值自然是全0。那到了这里我们已经很明确下面这一点了：
输入数据的每一位跟crc_init哪一位进行异或，只取决于该位的位置，而与该位数值本身，crc_init、crc_poly这些都无关，也就是只与位置有关而与数值无关。
同时我们要将CRC校验码生成函数做的两件事描述得更确切一些：
事情①：将输入数据的每一位与初始值的相应位进行异或（输入数据位宽大于CRC校验码位宽的则在初始值后面补0使其有足够的位跟输入数据的每一位对应）；
事情②：在循环里执行if判断语句块。
下面附上基于CRC模型2，16位输入的CRC校验码生成函数代码：

=======================
代码块11
=======================
#include <stdio.h>

unsigned char crc8_16bits_init0x00(unsigned short *data, unsigned int datalen){	
	unsigned short crc_init = 0x00;
	unsigned short crc_poly = 0x07;

	unsigned short crc_init16 = crc_init;
	crc_init16 = crc_init16 << 8;
	unsigned short crc_poly16 = crc_poly;
	crc_poly16 = crc_poly16 << 8;
	
	while (datalen--){	
		crc_init16 ^= (*(data++));
		for(int i=0;i<16;i++){   
			if(crc_init16 & 0x8000){
				crc_init16 = (crc_init16 << 1) ^ crc_poly16;
			}
			else{
				crc_init16 = (crc_init16 << 1) ^ 0x00;
			}
		}
	}
	crc_init = crc_init16 >> 8;
	return (crc_init);
}
int main(){
    unsigned short data_in[1] = {0xd9a8};
    unsigned char crc_out = crc8_16bits_init0x00(data_in,sizeof(data_in)/2);
    printf("crc_out = %#2x\n",crc_out);
    return 0;
}
=======================
运行结果：
crc_out = 0x56
=======================

运行结果与代码块5的相同，即将一个16位数据拆分为两个8位数据，然后将这两个8位数据先后输入到8位输入的CRC校验码生成函数，跟将一个16位数据输入到16位输入的CRC校验码生成函数，输出结果是一致的。佐证了上面的分析。
上面两种Verilog语言CRC校验码生成器之间的联系也是一样的，因为两种Verilog语言实现的CRC校验码生成器和8位输入的CRC校验码生成函数以及1位输入的CRC校验码生成函数是分别对应的，即代码块6和代码块3是对应的，代码块9和代码块10是对应的，而代码块8和代码块9又是逻辑等价变换的。
另外，基于上面的分析，我们就可以得到任意位宽数据的CRC校验码，比如对于一个n位数据，只要将这个数据拆分成一个个m位的数据（n不能被m整除则可在这个数据前面加上a个0让数据的位宽变成（n+a），使（n+a）能被m整除），然后将这些m位数据先后输入到m位输入的CRC校验码生成器即可，而不是只能将这个n位数据输入到n位输入的CRC校验码生成器里。

四、校验码的本质简述

1.理想的校验码生成器

理论上，对于一个校验码宽度为k的校验码生成器，我们最多有 $2^k$ 个校验码。那么对于同样位宽的校验码生成器来说，最理想的校验码生成器就是对于一个k位的数据能够产生 $2^k$ 个校验码。这样假设我们的数据码为k位，那么，我们的数据码的数值和每一个校验码将会是一一映射的关系，这样对于数据接收方，根据接收到的k位数据生成的校验码，将会知道实际接收到的数据具体是什么，再根据接收到的发送方根据这k位数据生成的校验码，假设接收到的校验码是正确的，那么接收方根据接收到的校验码就会知道发送方本来想要发送什么数据。这样就同时达到了校错和纠错的效果，完美完成了校验。
但用k位校验码去校验k位数据，也就是数据码和校验码宽度相同其实是不合理的，原因有两个：
1、让通信效率降低了一半。
2、校验码和数据码一样，在通信的过程当中，都会有被传输错误的风险，那么当校验码很长时，我们根本无法再去相信校验码本身。

2.数据校验应用的实际场景

(n,k)码理应适用于n远远大于k的情况。而对于这种情况，我们不可能达到k个校验码校验k个数据码的完美校错纠错效果。而数据校验本质上也不是为了达到这个完美校错纠错效果。
在理想情况下，我们的数据正常收发，并没有出现任何传输错误，我们是不需要对数据校验的。
极糟糕情况下，我们的数据在收发的过程中出现大量的传输错误，那说明我们的传输通道出了极大的问题，这个时候要考虑的就不是要校验数据了，而是搭好传输通道。
所以数据校验应该是应用于以下的情况：通信双方的传输通道比较理想，正常情况下是不会出现数据传输错误的情况，但因为通信双方实际的应用环境可能是很复杂的，有可能有些时候一些干扰会导致某一位或者某几位发生传输错误，这个时候数据校验才会派上用场。所以数据校验大多时候不需要让我们知道数据传输到底错在了哪，而是在数据传输错误的时候让通信接受方知道数据传输错误了。
对于一个比较理想的校验码生成器来说，n位数据在传输的过程中若发生了一位或者几位的传输错误，错误后的数据的校验码和这个n位数据本身的校验码一定不同或者相同几率极低，其实这就达到了比较完美的校错效果了。

3.一个好的CRC校验码生成器

基于上面的分析，那么我们要怎么得到一个好的CRC校验码生成器呢？文章到这里，我们已经知道，输入数据的每一位跟crc_init哪一位进行异或，只与位置有关而与数值无关，1位输入校验码生成器和n位输入校验码生成器的输出结果是一致的。而往往最底层的逻辑是最能说明问题的。
我们把目光放到LFSR模型上。对于一个LFSR模型，我们以不同的排列组合方式在不同的位之间安插异或门（这个异或门的功能就是让前一位的数据与fb_en异或得到下一位数据），这样的一种做法必然会让我们在给LFSR模型输入同样的数据时输出不一样的结果，即得到不一样的校验码。而对于同样宽度的一个数据，能让这些数据得到尽可能多的不同的校验码，那么这个就是一个相对比较好的CRC校验码生成器。而若是这个校验码生成器能够在数据码在传输过程当中发生了一位或者几位数据的错误时，两者的校验码一定不同或者相同几率极低，那么这就是一个好的CRC校验码生成器了。
而我们以不同的排列组合方式在不同的位之间安插异或门的这个做法，其实就是改变多项式即crc_poly的值，下面我们来直观感受下4位输入数据在不同crc_poly的CRC4校验码生成器下，会各自生成怎样的校验码，直接上C语言代码：

=======================
代码块12
=======================
#include <stdio.h>

unsigned char crc4_4bits(unsigned char *data, unsigned int datalen, unsigned char crc_poly)
{
	unsigned char crc_init = 0x0;

	while (datalen--) 	
	{
		crc_init ^= (*(data++));
		for(int i=0;i<4;i++){
			if(crc_init & 0x8){
				crc_init = (crc_init << 1) ^ crc_poly;
			}
			else{
				crc_init = crc_init << 1;
			}
		}
	}

	return (crc_init&0x0f);
}
int main(){
	unsigned char data_in[16];
	unsigned char data_out[16];
	unsigned char t;
	unsigned char cnt;
	printf("crc4_data_in: ");
	for(int i=0;i<sizeof(data_in);i++){
		data_in[i] = i;
		if(i == 0) printf("0x%#1x ",i);
		else printf("%#1x ",i);
	}
	printf("\n");
	for(int j=0;j<sizeof(data_in);j++){
    	unsigned char* data = data_in;
		if(j == 0) printf("crc4_poly0x%#1x: ",j);
		else printf("crc4_poly%#1x: ",j);
		for(int i=0;i<sizeof(data_in);i++){
			unsigned char crc_out = crc4_4bits(data,1,j);
			data_out[i] = crc_out;
			data++;
			if(crc_out==0) printf("0x%#1x ",crc_out);
			else printf("%#1x ",crc_out);
		}
		cnt = 0;
		for(int i=0;i<sizeof(data_out)-1;i++){
			t = i;
			while(sizeof(data_out)-1>t++){
				if(data_out[i] == data_out[t]) cnt++;
			}
		}
		if(cnt > 0) printf("repeat");
		printf("\n");
	}
	return 0;
}

输出结果：

crc4_data_in: 0x0 0x1 0x2 0x3 0x4 0x5 0x6 0x7 0x8 0x9 0xa 0xb 0xc 0xd 0xe 0xf 
crc4_poly0x0: 0x0 0x0 0x0 0x0 0x0 0x0 0x0 0x0 0x0 0x0 0x0 0x0 0x0 0x0 0x0 0x0 repeat
crc4_poly0x1: 0x0 0x1 0x2 0x3 0x4 0x5 0x6 0x7 0x8 0x9 0xa 0xb 0xc 0xd 0xe 0xf
crc4_poly0x2: 0x0 0x2 0x4 0x6 0x8 0xa 0xc 0xe 0x2 0x0 0x6 0x4 0xa 0x8 0xe 0xc repeat
crc4_poly0x3: 0x0 0x3 0x6 0x5 0xc 0xf 0xa 0x9 0xb 0x8 0xd 0xe 0x7 0x4 0x1 0x2
crc4_poly0x4: 0x0 0x4 0x8 0xc 0x4 0x0 0xc 0x8 0x8 0xc 0x0 0x4 0xc 0x8 0x4 0x0 repeat
crc4_poly0x5: 0x0 0x5 0xa 0xf 0x1 0x4 0xb 0xe 0x2 0x7 0x8 0xd 0x3 0x6 0x9 0xc
crc4_poly0x6: 0x0 0x6 0xc 0xa 0xe 0x8 0x2 0x4 0xa 0xc 0x6 0x0 0x4 0x2 0x8 0xe repeat
crc4_poly0x7: 0x0 0x7 0xe 0x9 0xb 0xc 0x5 0x2 0x1 0x6 0xf 0x8 0xa 0xd 0x4 0x3
crc4_poly0x8: 0x0 0x8 0x8 0x0 0x8 0x0 0x0 0x8 0x8 0x0 0x0 0x8 0x0 0x8 0x8 0x0 repeat
crc4_poly0x9: 0x0 0x9 0xb 0x2 0xf 0x6 0x4 0xd 0x7 0xe 0xc 0x5 0x8 0x1 0x3 0xa
crc4_poly0xa: 0x0 0xa 0xe 0x4 0x6 0xc 0x8 0x2 0xc 0x6 0x2 0x8 0xa 0x0 0x4 0xe repeat
crc4_poly0xb: 0x0 0xb 0xd 0x6 0x1 0xa 0xc 0x7 0x2 0x9 0xf 0x4 0x3 0x8 0xe 0x5
crc4_poly0xc: 0x0 0xc 0x4 0x8 0x8 0x4 0xc 0x0 0xc 0x0 0x8 0x4 0x4 0x8 0x0 0xc repeat
crc4_poly0xd: 0x0 0xd 0x7 0xa 0xe 0x3 0x9 0x4 0x1 0xc 0x6 0xb 0xf 0x2 0x8 0x5
crc4_poly0xe: 0x0 0xe 0x2 0xc 0x4 0xa 0x6 0x8 0x8 0x6 0xa 0x4 0xc 0x2 0xe 0x0 repeat
crc4_poly0xf: 0x0 0xf 0x1 0xe 0x2 0xd 0x3 0xc 0x4 0xb 0x5 0xa 0x6 0x9 0x7 0x8

从输出结果可以看到，当输入数据的数值分别为0-15时，多项式为偶数的CRC4校验码生成函数输出的校验码有重复，多项式为奇数的CRC4校验码生成函数输出的校验码没有重复，那么很显然多项式为奇数的CRC4校验码生成器是相对较好的CRC4校验码生成器。这也是为什么我们平时用的CRC校验码模型的多项式要求最低位为1。
关于这其中的原理以及怎样找到最合适的CRC校验码模型，就需要额外去研究了，这里就不再赘述。

4.为什么CRC校验码的生成要将输入数据与初始值对应位异或？

在文章的最后，说回前面提的一个问题：为什么CRC校验码的生成要将输入数据与初始值对应位异或？
我们还是把目光放到LFSR模型上。我们先来看下基于LFSR模型实现的伪随机码生成器，对于一个n位伪随机码生成器，我们只需要load一个随机种子进去，剩下的它自己就可以在每次时钟来临的时候输出一次数据，数据以 $2^n$ 为周期循环输出。
而对于CRC校验码生成器，我们是需要输入不同位宽不同数值的数据来生成一个校验码，所以需要我们的fb_en不但要取决于Q $\scriptstyle n$ 还要取决于输入数据，即需要fb_en = crc_out[n] ^ data_in[i]，而当我们的CRC校验码生成器电路定下来了之后，我们将得到一个映射f：X $\rarr$ Y，其中data_in $\in$ X，CRC校验码 $\in$ Y。这就是CRC校验码的生成需要将输入数据与初始值对应位异或的原因。