1. Toy模板网首页
  2. > Toy博客

二叉树的遍历（节点个数及层序遍历）

9月前 作者：Wei&Yan 分类：Toy博客 阅读(51) 违法举报

这篇具有很好参考价值的文章主要介绍了二叉树的遍历（节点个数及层序遍历）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

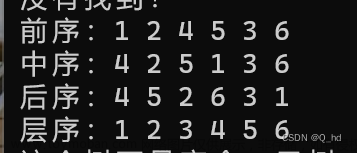
 简易树的图形：

二叉树的遍历（节点个数及层序遍历）

 

#include <stdio.h>
#include  <stdlib.h>

//重定义数据类型
typedef char DataType;
//创建简易的二叉树结构体
typedef struct BTNode
{
	struct BTNode* left;
	struct BTNode* right;
	DataType data;
}BTNode;
//前序（根左右）
void Prev(BTNode* root)
{
	//判空
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	printf("%c ", root->data);
	Prev(root->left);
	Prev(root->right);
}
//中序（左根右）
void Inmid(BTNode* root)
{
	//判空
	if (root == NULL)
	{
		printf("NULL ");
		return 0;
	}
	Inmid(root->left);
	printf("%c ", root->data);
	Inmid(root->right);
}
//后序（左右根）
void Pose(BTNode* root)
{
	//判空
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	Pose(root->right);
	printf("%c ", root->data);
	Pose(root->left);
}
//返回节点个数
int TreeSize(BTNode* root)
{
	return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
//初始化以及赋值树
int main()
{
	BTNode* A = (BTNode*)malloc(sizeof(BTNode));
	A->left = NULL;
	A->right = NULL;
	A->data = 'A';
	BTNode* B = (BTNode*)malloc(sizeof(BTNode));
	B->left = NULL;
	B->right = NULL;
	B->data = 'B';
	BTNode* C = (BTNode*)malloc(sizeof(BTNode));
	C->left = NULL;
	C->right = NULL;
	C->data = 'C';
	BTNode* D = (BTNode*)malloc(sizeof(BTNode));
	D->left = NULL;
	D->right = NULL;
	D->data = 'D';
	BTNode* E = (BTNode*)malloc(sizeof(BTNode));
	E->left = NULL;
	E->right = NULL;
	E->data = 'E';
	//赋值
	A->data = 'A';
	A->left = B;
	A->right = C;
	B->data = 'B';
	B->left = D;
	B->right = E;
	/*Prev(A);
	printf("\n");
	Inmid(A);
	printf("\n");*/
	printf("TreeSize:%d\n", TreeSize(A));
	printf("TreeSize:%d\n", TreeSize(B));
	return 0;
}

 运行实例：

以A节点开始运算的节点个数

以B节点开始运算的节点个数

二叉树的遍历（节点个数及层序遍历）

解释（图解+文字解释）： 

把A传过去A不为空，进入left，A的left为B不为空，B的left为D不为空，D的left和right都为空返回0+0+1，在进入B的right，B的right为E不为空，E的left和right都为空返回0+0+1，B的left和right都返回1，运行完B，B再返回1+1+1=3，再进入A right->C,Cleft,right都为空返回1，最后A返回left（3）+right（1）+1=5.

 二叉树的遍历（节点个数及层序遍历）

 求叶子节点个数：

//叶子节点的个数
int TreeLeafSize(BTNode* root)
{
	if (root = NULL)
		return 0;
	if (root->left == NULL && root->right == NULL)
		return 1;
	return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}

二叉树的遍历（节点个数及层序遍历）

 传A过去，先判断A不为空，也不为叶子，则返回A的left+right，进入left为B，不为空和叶子，返回B的left和right，进入B left为D为叶子返回1，再进入B的right为E叶子返回1，则B返回2，在进入A的right C，C为叶子返回1，最终A返回3.

 

注意：（计算节点麻烦的用法）

1.定义全局变量来统计

因为要每次把size归零比较麻烦

二叉树的遍历（节点个数及层序遍历）

二叉树的遍历（节点个数及层序遍历） 

二叉树的遍历（节点个数及层序遍历） 

 2.传地址

传地址过去然后每次遇见一个节点++

二叉树的遍历（节点个数及层序遍历）

 

二叉树的遍历（节点个数及层序遍历） 

 

 层序遍历法：（符合队列的先进先出）

概念：及从第一行开始，一行一行的统计，每行从左到右，如我们最开始的例图层序遍历完后为ABCDE。

举例解释：

二叉树的遍历（节点个数及层序遍历）

 

 二叉树的遍历（节点个数及层序遍历）

 

 讲解：先代入A，A不为空，拿出A且代入A的子节BC，B不为空，拿出B再代入B的子节DE，C不为空拿出C再代入C的子节FG，D不为空拿出（D没有子节不用带入了），E不为空拿出，代入E的子节H，FGH都不为空且都没有子节了再依次拿出到空为止。

实现：

 头文件：

#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>
//前置声明（防止头文件Quene.h在2复制过去后往上找的时候找不到我们创建的树的结构体BTNode）
struct BTNode;

//重命名类型
typedef struct BTNode* QDataType;
//创建队列结构体
typedef struct QueueNode
{
	struct QueueNode* next;
	QDataType data;
}QNode;
//创建指针
typedef struct Queue
{
	QNode* head;
	QNode* tail;
}Queue;

//初始化
void QueueInit(Queue* pq);
//销毁
void QueueDestory(Queue* pq);
//队尾入队列
void QueuePush(Queue* pq,QDataType x);
//队头出队列
void QueuePop(Queue* pq);
//取数据队头
QDataType QueueFront(Queue* pq);
//取数据队尾
QDataType QueueBack(Queue* pq);
//数据的有效值
int QueueSize(Queue* pq);
//判空
bool QueueEmpty(Queue* pq);

队列文件：

#include "Queue.h"

//初始化
void QueueInit(Queue* pq)
{
	assert(pq);
	pq->head = pq->tail = NULL;
}
//销毁
void QueueDestory(Queue* pq)
{
	assert(pq);
	QNode* cur=pq->head;
	while (cur)
	{
		QNode* next = cur->next;//先保存下一个再释放自己，再让next赋值给cur
		free(cur);
		cur = next;
	}
	//结束后再把head和tail置空
	pq->head = pq->tail = NULL;
}
//队尾入队列
void QueuePush(Queue* pq, QDataType x)
{
	assert(pq);
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}
	else
	{
		newnode->data = x;
		newnode->next = NULL;
	}
	if (pq->tail==NULL)
	{
		pq->head = pq->tail = newnode;
	}
	else
	{
		pq->tail->next = newnode;
		pq->tail = newnode;
	}
}
//队头出队列
void QueuePop(Queue* pq)
{
	assert(pq);
	assert(pq->head);
	if (pq->head->next == NULL)//这里我们要判断一下head的next是否为空，如果为空说明只有一个节点了，我们直接释放，否则tail变成了野指针
	{
		free(pq->head);
		pq->head = pq->tail = NULL;
	}
	else
	{
		QNode* next = pq->head->next;
		free(pq->head);
		pq->head = next;
	}
}
//取数据队头
QDataType QueueFront(Queue* pq)
{
	assert(pq);
	assert(pq->head);//先判断头是否已经为空
	return pq->head->data;
}
//取数据队尾
QDataType QueueBack(Queue* pq)
{
	assert(pq);
	return pq->tail->data;
}
//数据的有效值
int QueueSize(Queue* pq)
{
	assert(pq);
	int size = 0;
	QNode* cur = pq->head;
	while (cur)//我们直接遍历一遍知道cur为空的时候停止
	{
		size++;
		cur = cur->next;
	}
	return size;
}
//判空
bool QueueEmpty(Queue* pq)
{
	assert(pq);
	return pq->head == NULL;//判断如果为空则返回真，否则为假
}

树文件

#include <stdio.h>
#include  <stdlib.h>
#include "Queue.h"
//重定义数据类型
typedef char DataType;
//创建简易的二叉树结构体
typedef struct BTNode
{
	struct BTNode* left;
	struct BTNode* right;
	DataType data;
}BTNode;
//前序（根左右）
void Prev(BTNode* root)
{
	//判空
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	printf("%c ", root->data);
	Prev(root->left);
	Prev(root->right);
}
//中序（左根右）
void Inmid(BTNode* root)
{
	//判空
	if (root == NULL)
	{
		printf("NULL ");
		return 0;
	}
	Inmid(root->left);
	printf("%c ", root->data);
	Inmid(root->right);
}
//后序（左右根）
void Pose(BTNode* root)
{
	//判空
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	Pose(root->right);
	printf("%c ", root->data);
	Pose(root->left);
}
//返回节点个数
int TreeSize(BTNode* root)
{
	return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
//叶子节点的个数
int TreeLeafSize(BTNode* root)
{
	if (root = NULL)
		return 0;
	if (root->left == NULL && root->right == NULL)
		return 1;
	return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}
//层序遍历
void LevelOrder(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root)//如果队列为空则入值
		QueuePush(&q, root);
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q); 
		QueuePop(&q);//取出来
		printf("%c ", front->data);
		if (front->left)
		{
			QueuePush(&q, front->left);
		}if (front->right)
		{
			QueuePush(&q, front->right);
		}
	}
	printf("\n");
	QueueDestory(&q);
}
//初始化以及赋值树
int main()
{
	BTNode* A = (BTNode*)malloc(sizeof(BTNode));
	A->left = NULL;
	A->right = NULL;
	A->data = 'A';
	BTNode* B = (BTNode*)malloc(sizeof(BTNode));
	B->left = NULL;
	B->right = NULL;
	B->data = 'B';
	BTNode* C = (BTNode*)malloc(sizeof(BTNode));
	C->left = NULL;
	C->right = NULL;
	C->data = 'C';
	BTNode* D = (BTNode*)malloc(sizeof(BTNode));
	D->left = NULL;
	D->right = NULL;
	D->data = 'D';
	BTNode* E = (BTNode*)malloc(sizeof(BTNode));
	E->left = NULL;
	E->right = NULL;
	E->data = 'E';
	//赋值
	A->data = 'A';
	A->left = B;
	A->right = C;
	B->data = 'B';
	B->left = D;
	B->right = E;
	/*Prev(A);
	printf("\n");
	Inmid(A);
	printf("\n");*/
	printf("TreeSize:%d\n", TreeSize(A));
	printf("TreeSize:%d\n", TreeSize(B));
	LevelOrder(A);
	return 0;
}

 

 二叉树的遍历（节点个数及层序遍历）文章来源地址https://www.toymoban.com/news/detail-421332.html

到了这里，关于二叉树的遍历（节点个数及层序遍历）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处： 如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！

分享到：
领支付宝红包 赞助服务器费用

相关文章

  • ★102. 二叉树的层序遍历

    ★102. 二叉树的层序遍历

    很巧妙的，又学习了一种层次遍历的方法， 就是说根据当前的队列的长度去遍历，遍历的当前队列的长度就是该层次的节点个数。

    2024年02月05日
    浏览(43)
  • 41 二叉树的层序遍历

    41 二叉树的层序遍历

    给你二叉树的根节点 root ，返回其节点值的 层序遍历 。 （即逐层地，从左到右访问所有节点）。 提示： 树中节点数目在范围 [0, 2000] 内 -1000 = Node.val = 1000

    2024年02月07日
    浏览(46)
  • 二叉树题目：二叉树的层序遍历 II

    二叉树题目：二叉树的层序遍历 II

    标题：二叉树的层序遍历 II 出处：107. 二叉树的层序遍历 II 4 级 要求 给你二叉树的根结点 root texttt{root} root ，返回其结点值自底向上的层序遍历（即从左到右，按从叶结点所在层到根结点所在层逐层遍历）。 示例 示例 1： 输入： root   =   [3,9,20,null,null,15,7] texttt{root = [3

    2024年02月11日
    浏览(35)
  • 【C++】102.二叉树的层序遍历

    【C++】102.二叉树的层序遍历

    给你二叉树的根节点 root ，返回其节点值的 层序遍历 。 （即逐层地，从左到右访问所有节点）。 示例1： 示例 2： 示例 3： 提示： 树中节点数目在范围 [0, 2000] 内 -1000 = Node.val = 1000 这个问题实际上可以只用一个队列就实现，只需要再增加一个变量 levelSize ，用来记录每一层

    2024年03月11日
    浏览(48)
  • 算法进阶——求二叉树的层序遍历

    算法进阶——求二叉树的层序遍历

    题目 给定一个二叉树，返回该二叉树层序遍历的结果，（从左到右，一层一层地遍历）。 例如： 给定的二叉树是{3,9,20,#,#,15,7}, 该二叉树层序遍历的结果是 [ [3], [9,20], [15,7] ] 提示: 0 = 二叉树的结点数 = 1500 示例1 示例2 思路 利用辅助队列，通过bfs（广度优先）算法遍历二叉树

    2024年01月24日
    浏览(45)
  • 【数据结构】二叉树的层序遍历

    【数据结构】二叉树的层序遍历

    当我们面对一个树结构时，常常需要对其进行遍历以获取其中的节点信息。其中一种常用的遍历方式是层序遍历，也称为广度优先搜索（BFS）。本篇博客将详细介绍层序遍历的原理和实现方法。 层序遍历以树的根节点开始，按照从上到下、从左到右的顺序逐层遍历树中的节点

    2024年02月03日
    浏览(45)
  • 【LeetCode】102.二叉树的层序遍历

    【LeetCode】102.二叉树的层序遍历

    给你二叉树的根节点  root  ，返回其节点值的  层序遍历  。 （即逐层地，从左到右访问所有节点）。 示例 1： 示例 2： 示例 3： 提示： 树中节点数目在范围  [0, 2000]  内 -1000 = Node.val = 1000 之前做的题里深度优先遍历（DFS）用得比较多，主要是回溯算法，这道题的层序遍

    2024年02月15日
    浏览(41)
  • day-20 二叉树的层序遍历

    day-20 二叉树的层序遍历

    思路：利用队列进行广度优先遍历即可 注意点：ArrayList执行remove之后，索引i会立即重排，注意可能越界 code:

    2024年03月19日
    浏览(49)
  • LeetCode 0103.二叉树的锯齿形层序遍历：层序遍历 + 适时翻转

    LeetCode 0103.二叉树的锯齿形层序遍历：层序遍历 + 适时翻转

    力扣题目链接：https://leetcode.cn/problems/binary-tree-zigzag-level-order-traversal/ 给你二叉树的根节点 root ，返回其节点值的 锯齿形层序遍历 。（即先从左往右，再从右往左进行下一层遍历，以此类推，层与层之间交替进行）。   示例 1： 示例 2： 示例 3：   提示： 树中节点数目在范

    2024年02月20日
    浏览(39)
  • 【数据结构】二叉树的层序遍历（四）

    【数据结构】二叉树的层序遍历（四）

     目录 一，层序遍历概念 二，层序遍历的实现         1，层序遍历的实现思路         2，创建队列         Queue.h         Queue.c         3，创建二叉树         BTree.h         BTree.c         4，层序遍历的实现 层序遍历：除了先序遍历、中序遍历、

    2024年02月07日
    浏览(47)

觉得文章有用就打赏一下文章作者

支付宝扫一扫打赏

博客赞助

微信扫一扫打赏

请作者喝杯咖啡吧~博客赞助

支付宝扫一扫领取红包，优惠每天领

二维码1

领取红包

二维码2

领红包