动态规划机试2023.4.19-Toy模板网

这篇具有很好参考价值的文章主要介绍了动态规划机试2023.4.19。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

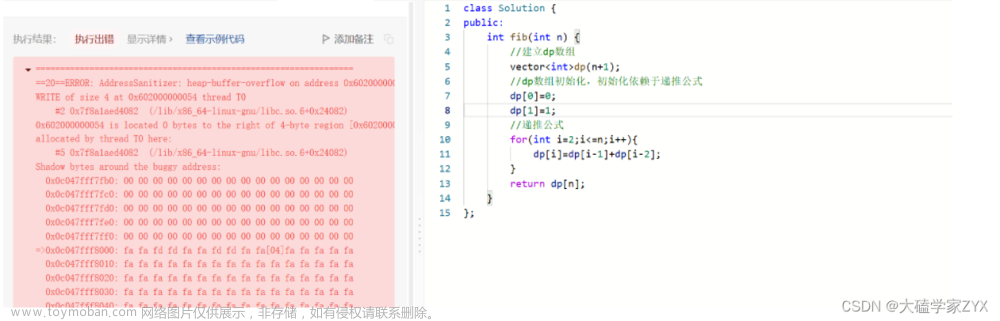
eg12.1 N阶楼梯上楼问题

#include <bits/stdc++.h>
#include <ios>
const int N=100;
int dp[N];
using namespace std;
int main()
{
    ios_base::sync_with_stdio(0);
    cin.tie(0),cout.tie(0);
    int n;
    cin>>n;
    dp[0]=1;
    dp[1]=1;
    dp[2]=2;
    for(int i=3;i<=n;i++)
    {
        dp[i]=dp[i-1]+dp[i-2];
    }
    cout<<dp[n]<<endl;
    return 0;
}

ex12.1 吃糖果和（eg12.1的程序一模一样）

eg12.2 最大序列和

#include <bits/stdc++.h>
#include <climits>
using namespace std;
typedef long long LL;
const int N=1000010;
const int INF=INT_MAX;
LL dp[N],a[N];
int main()
{
   int n;
   while(cin>>n)
   {
      memset(dp,0,sizeof dp);
      for(int i=0;i<n;i++) cin>>a[i];
      //dp[i]的含义是以下标为i-1结尾的非空连续序列的最大序列和
      dp[0]=a[0];
      LL res=-1*INF;
      for(int i=1;i<n;i++)
      {
        dp[i]=max(dp[i-1]+a[i],a[i]);
        res=max(res,dp[i]);
      }
      cout<<res<<endl;
   }
   return 0;
}

eg12.3 最大子矩阵（北京大学复试上机题）

复习了二维前缀和并且使用暴力做法解出该题

#include <bits/stdc++.h>
using namespace std;
const int N=101;
const int INF=INT_MAX;
int a[N][N],s[N][N];

int main()
{
	int n;
	while(cin>>n)
	{
		memset(a,0,sizeof a);
		memset(s,0,sizeof s);
		for(int i=0;i<n;i++)
		{
			for(int j=0;j<n;j++)
			{
				cin>>a[i][j];
			}
		}
		s[0][0]=a[0][0];
		for(int i=1;i<n;i++) s[i][0]=s[i-1][0]+a[i][0];
		for(int j=1;j<n;j++) s[0][j]=s[0][j-1]+a[0][j];
		for(int i=1;i<n;i++)
		{
			for(int j=1;j<n;j++)
			{
		      s[i][j]+=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];		
			}
		} 
		int res=-1*INF;
		for(int x1=0;x1<n;x1++)
		{
			for(int y1=0;y1<n;y1++)
			{
				for(int x2=x1;x2<n;x2++)
				{
					for(int y2=y1;y2<n;y2++)
					{
						int tmp=s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1];
						res=max(res,tmp);
					}
				}
			}
		}
		cout<<res<<endl;
	}
	
	return 0;
}

ex12.2 最大连续子序列（浙江大学复试上机题）

使用前缀和

#include <bits/stdc++.h>
using namespace std;
const int N=10010;
const int INF=INT_MAX;
int a[N],s[N];//求前缀和

int main()
{
  int n;
  while(cin>>n)
  {
     if(n==0) break;
	 for(int i=0;i<n;i++) cin>>a[i];
	 s[0]=a[0];
	 for(int i=1;i<n;i++) s[i]=s[i-1]+a[i];
	 int res=-1*INF,resx,resy;
	 for(int x=0;x<n;x++)
	 {
	    for(int y=x;y<n;y++)
		{
		   int tmp=s[y]-s[x-1];
		   if(tmp>res) 
		   {
		   	  res=tmp;
		   	  resx=a[x];
		   	  resy=a[y];
		   }
		}	
	 }
	 cout<<res<<" "<<resx<<" "<<resy<<endl;	
  }   
  return 0;	
}

eg12.4 拦截导弹（北京大学复试上机题）

最大不增子序列

//最长不增子序列
#include <bits/stdc++.h>
using namespace std;
const int N=100010;
int a[N];
int dp[N];

int main()
{
	ios_base::sync_with_stdio(0);
	cin.tie(0),cout.tie(0);

	int n;
	cin>>n;
	for(int i=0;i<n;i++) cin>>a[i];
	//dp[i]代表以第下标为i的元素结尾的最长不增子序列的长度 
    int res=0;
	for(int i=0;i<n;i++)
	{	
        dp[i]=1;
	    for(int j=0;j<i;j++)
		{
		  if(a[j]>=a[i])
		  {
		    dp[i]=max(dp[i],dp[j]+1);	
		  }
		}
		res=max(res,dp[i]);	
	} 
	cout<<res<<endl;
	return 0;
}

eg12.5 最大上升子序列和（北京大学复试上机题）

#include <bits/stdc++.h>
#include <ios>
using namespace std;
const int N=1010;
int a[N];
int dp[N];

int main()
{
    ios_base::sync_with_stdio(0);
    cin.tie(0),cout.tie(0);

    int n;
    while(cin>>n)
    {
        for(int i=0;i<n;i++) cin>>a[i];
        int res=0;
        for(int i=0;i<n;i++) 
        {
            dp[i]=a[i];//初始化dp
            for(int j=0;j<i;j++)
            {
                if(a[j]<a[i])
                {
                    dp[i]=max(dp[i],dp[j]+a[i]);
                    res=max(res,dp[i]);
                }
            }
        }
       cout<<res<<endl;
    }
    
    return 0;
}

ex12.3 合唱队形（北京大学复试上机题）

分析：首先从前往后寻找以i点为尾的最长递增子列，再从后往前寻找以i点为尾的最长递增子列，寻找点i两个子列和的最大值

代码如下：

#include <bits/stdc++.h>
using namespace std;
const int N=101;
int a[N],dp1[N],dp2[N];

int main()
{
    int n;
    while(cin>>n)
    {
        if(n==0) break;
        for(int i=0;i<n;i++) cin>>a[i];
        
        for(int i=0;i<n;i++)
        {
            dp1[i]=1;
            for(int j=0;j<i;j++)
            {
                if(a[j]<a[i])
                {
                    dp1[i]=max(dp1[i],dp1[j]+1);
                }
            }
        }
        for(int i=n-1;i>=0;i--)
        {
            dp2[i]=1;
            for(int j=n-1;j>i;j--)
            {
                if(a[j]<a[i])
                {
                    dp2[i]=max(dp2[i],dp2[j]+1);
                }
            }
        }
        int res=1;
        for(int i=0;i<n;i++)
        {
            res=max(res,dp1[i]+dp2[i]);
        }
        cout<<n-res+1<<endl;
    }
    return 0;
}

eg12.6 Common Subsequence

//最长公共子序列
#include <bits/stdc++.h>
using namespace std;
const int N=1001;
char s1[N];
char s2[N];
int dp[N][N];
//dp[i][j]代表以下标i-1结尾的字符串1的子串和以下标为j-1结尾的字符串2的子串的最长公共长度 
int main()
{
    ios_base::sync_with_stdio(0);
    cin.tie(0),cout.tie(0);  
    //string s1,s2;
	while(scanf("%s%s",s1+1,s2+1)!=EOF)
	//while(getline(cin,s1)&&getline(cin,s2))
	{
		int n=strlen(s1+1);
		int m=strlen(s2+1);
		int res=0;
		for(int i=0;i<=n;i++)
		{
			for(int j=0;j<=m;j++)
			{
				if(i==0||j==0)
				{
					dp[i][j]=0;
					continue;
				}
				if(s1[i]==s2[j])
				  dp[i][j]=dp[i-1][j-1]+1;
				else 
				  dp[i][j]=max(dp[i-1][j],dp[i][j-1]); 
			}
		}
		cout<<dp[n][m]<<endl;
	}	
}

ex12.4 Coincidence(上海交通大学复试上机题）

#include <iostream>
#include <string>
#include <vector>
#include <string.h>
using namespace std;

string getLongestSubStr(string& str1, string& str2){
    int start = 0;
    int maxSub = 0;
    
    if(str1.size()>str2.size()){
        swap(str1, str2);
    }
    
    vector< vector<int> > vv(str1.size()+1, vector<int>(str2.size()+1,0));
    for(int i=1; i<=str1.size(); ++i){
        for(int j=1; j<=str2.size(); ++j){
            if(str1[i-1] == str2[j-1]){
                vv[i][j] = vv[i-1][j-1]+1;
            }
            if(vv[i][j] > maxSub){
                maxSub = vv[i][j];
                start = i-maxSub;
            }
        }       
    }
    return str1.substr(start, maxSub);
}

int main(){
    
    string str1,str2;
    while(cin>>str1>>str2){
        string s = getLongestSubStr(str1, str2);
        cout<<s<<endl;
    }
    
    return 0;
}

01背包模板

#include <bits/stdc++.h>
using namespace std;
const int N=100010;
int weight[N],value[N];
int dp[N];
int main()
{
    ios_base::sync_with_stdio(0);
    cin.tie(0),cout.tie(0);
    
    int n,m;
    cin>>n>>m;
    for(int i=0;i<n;i++) cin>>weight[i]>>value[i];
    
    for(int i=0;i<n;i++)
    {
        for(int j=m;j>=weight[i];j--)
         dp[j]=max(dp[j],dp[j-weight[i]]+value[i]);
    }
    cout<<dp[m]<<endl;
    return 0;
}

完全背包模板

#include <bits/stdc++.h>
using namespace std;
const int N=100010;
int weight[N],value[N];
int dp[N];

int main()
{
    ios_base::sync_with_stdio(0);
    cin.tie(0),cout.tie(0);
    int n,m;
    cin>>n>>m;
    for(int i=0;i<n;i++) cin>>weight[i]>>value[i];
    
    for(int i=0;i<n;i++)
    {
       for(int j=weight[i];j<=m;j++)
       {
            dp[j]=max(dp[j],dp[j-weight[i]]+value[i]);
       }
    }
    cout<<dp[m]<<endl;
    return 0;
}

多重背包模板文章来源地址https://www.toymoban.com/news/detail-421387.html

#include <bits/stdc++.h>
using namespace std;
const int N=101;
int weight[N],value[N],nums[N];
int dp[N][N];

int main()
{
    ios_base::sync_with_stdio(0);
    cin.tie(0),cout.tie(0);
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>weight[i]>>value[i]>>nums[i];
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
           for(int k=0;k<=nums[i]&&k*weight[i]<=j;k++)
            dp[i][j]=max(dp[i][j],dp[i-1][j-k*weight[i]]+k*value[i]);
        }
    }
    cout<<dp[n][m]<<endl;
    return 0;
}

到了这里，关于动态规划机试2023.4.19的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！