数据结构与算法学习：二叉树的后序遍历的递归与非递归实现，以及非递归实现中的流程控制的说明。-Toy模板网

这篇具有很好参考价值的文章主要介绍了数据结构与算法学习：二叉树的后序遍历的递归与非递归实现，以及非递归实现中的流程控制的说明。。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

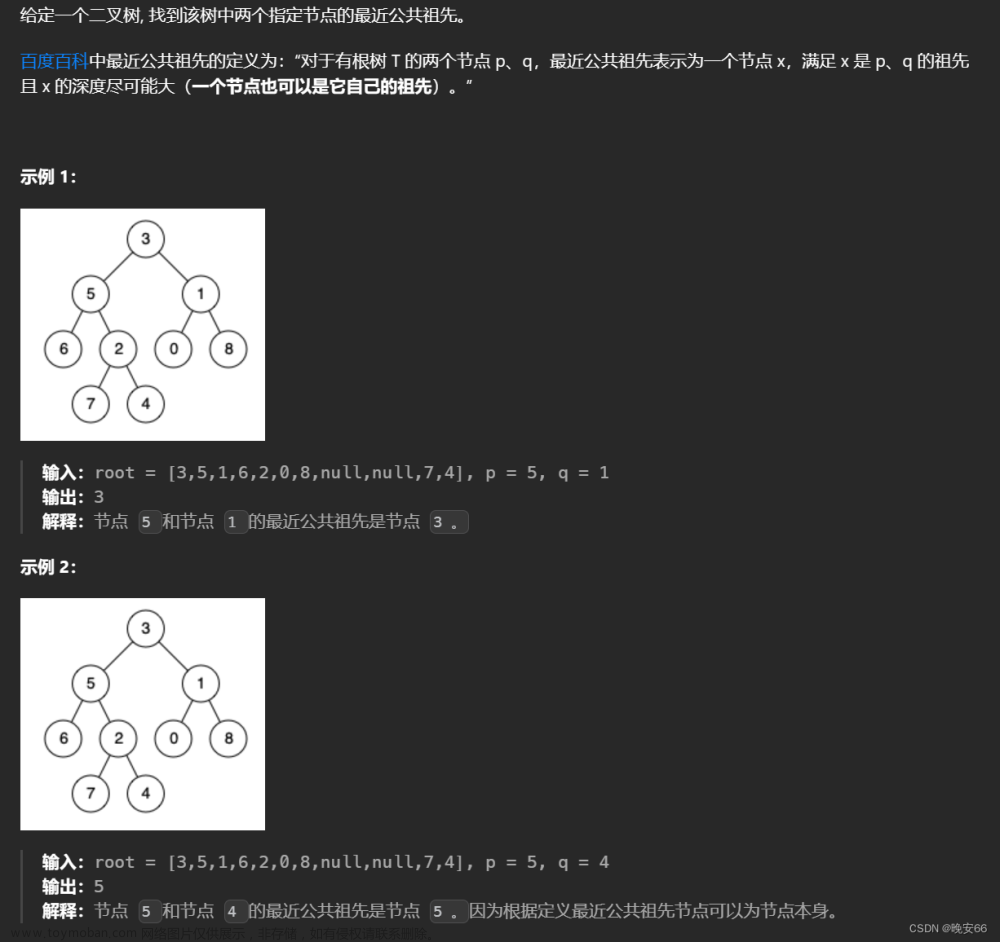
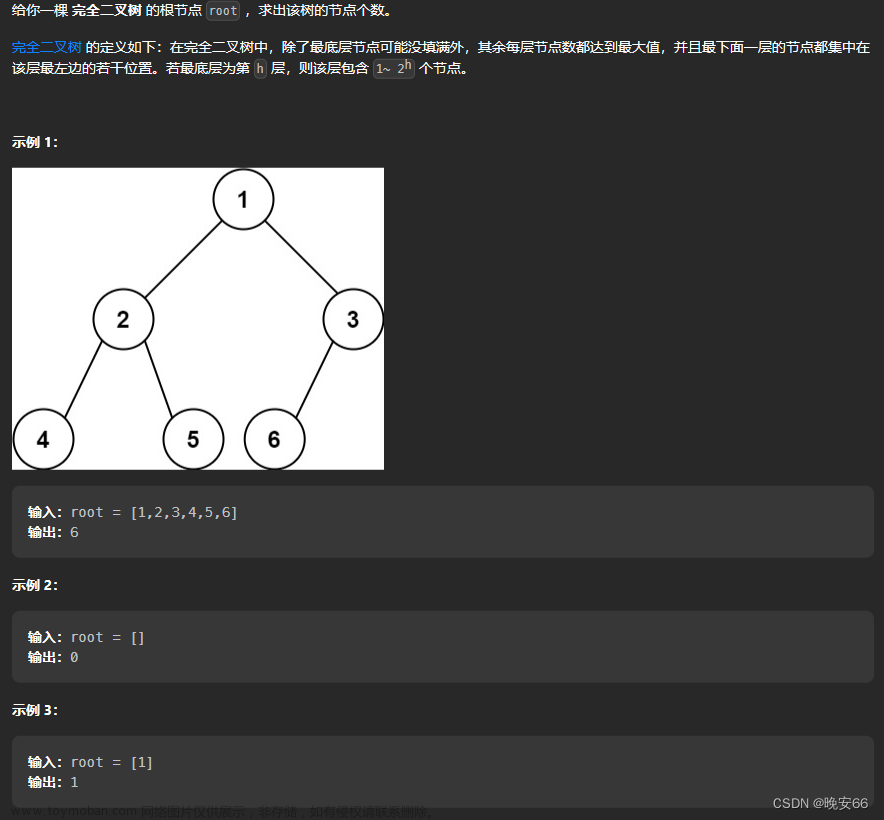
需求二叉树：

数据结构与算法学习：二叉树的后序遍历的递归与非递归实现，以及非递归实现中的流程控制的说明。

采用二叉树后序遍历非递归算法。设置一个指针p初始指向树根，p先入栈，而后使得p指向它的左孩子p->firstchild，重复操作，使得每个左孩子都依次入栈，同时初始化一个Treenode*类型的指针pre，这个指针是后序前驱，这个后序前驱用以区分为已访问过的结点和未访问过的结点。

由于栈顶元素一定是某一子树的根，那么先假设p==S.top()我们把叶子结点等价为左右孩子都为空的子树的根作为分析时的假设，想要访问栈顶元素那么要么右子树为空，要么右子树被访问完为空好办，核心的流程控制就在于右子树访问完这里的问题，根据后续遍历的性质又知道，因为先前设置pre为上一步刚访问过的结点，即后序前驱，如果右子树被访问完那么就意味着p->nextchild==后序前驱，而这个后序前驱就是pre，要是p=p->nextchild，而后右设置pre=p，而p->nextchild==pre...那么就会在pre那里死循环。所以，能让p=p->nextchild;的条件就是(p->nextchild!=NULL&&p->nextchild!=后序前驱)若p->nextchild!=NULL不和后一个条件相与会形成访问某一个结点的右子树的死循环。

后序遍历非递归算法的流程控制较为复杂，以上为流程控制中条件判断的确定方法，下面给出算法流程：

①沿着根的左孩子依次入栈

②直到左孩子为空读栈顶元素若其右孩子不空且未被访问过将右子树转执行①否则栈顶元素出栈并访问。

”tree.hpp":

#define _CRT_SECURE_NO_WARNINGS 1

#include <stdbool.h>
#include <iostream>
#include <stdlib.h>
#include <ctime>
#include <stack>
#include<queue>
using namespace std;


class Treenode
{
	friend class Bitree;
public:
	
	Treenode();
	Treenode(char a);
	//Treenode(char c);
	Treenode& setnode(char a)
	{
		this->val = a;
		return *this;
	}

	void setfirstchild(Treenode* a);
	void setnextchild(Treenode* a);
	void setrtag(bool a);
	void setltag(bool a);
	char getval();
	Treenode& getfirstchild();
	Treenode& getnextchild();

private:
	
	char val;//数据部分
	Treenode* firstchild;
	Treenode *nextchild;//同一化的树的存储
	bool ltag , rtag ;//0表示有左或右孩子，1表示该结点没有左或右孩子，且此链域是线索

};

Treenode& Treenode::getfirstchild()
{
	return *this->firstchild;
}
Treenode& Treenode::getnextchild()
{
	return *this->nextchild;
}
char Treenode::getval()
{
	return this->val;
}
void Treenode::setfirstchild(Treenode* a)
{
	this->firstchild = a;
}
void Treenode::setnextchild(Treenode *a)
{
	this->nextchild = a;
}

void Treenode::setltag(bool a)
{
	this->ltag = a;
}
void Treenode::setrtag(bool a)
{
	this->rtag = a;
}
Treenode::Treenode(char a)
{
	this->val = a;
	if (this->firstchild != NULL)
	{
		delete this->firstchild;
	}
	this->firstchild = NULL;
	if (this->nextchild != NULL)
	{
		delete this->nextchild;
	}
	this->nextchild = NULL;
	this->ltag = false;
	this->rtag = false;
}
Treenode::Treenode()
{
	this->val = '#';
	if (this->firstchild != NULL)
	{
		delete this->firstchild;
	}
	this->firstchild = NULL;
	if (this->nextchild != NULL)
	{
		delete this->nextchild;
	}
	this->nextchild = NULL;
	this->ltag = false;
	this->rtag = false;
}



class Bitree
{
	friend class Treenode;
public:
	Bitree()
	{
		this->root = new(class Treenode);
	}
	Treenode& setroot(Treenode* a);

	void visit(Treenode* a);
	Treenode* getroot()
	{
		return this->root;
	}
	

	
	int getcount()
	{
		return this->count;
	}


	void postorder_traversal(Treenode* t);//后序遍历
	void postorder_nonrecursion_traversal();//后序非递归算法
private:
	Treenode* root;
	int count = 0;
};

void Bitree::postorder_traversal(Treenode* t)//后序遍历
{
	if (t == NULL)
		return;
	postorder_traversal(t->firstchild);
	postorder_traversal(t->nextchild);
	this->visit(t);
}
void Bitree::postorder_nonrecursion_traversal()//后序非递归算法
{
	stack<Treenode*> S;
	Treenode* p = this->root;
	Treenode* pre = NULL;//最近访问过的结点,后序前驱
	while (p || !S.empty())
	{
		if (p)
		{
			S.push(p);
			p = p->firstchild;
		}
		else 
		{
			p = S.top();//只有当前p为空才使它指向栈顶元素
			if (p->nextchild && p->nextchild != pre)//为什么要设置一个最近访问过的结点r？
				p = p->nextchild;//上面的p->nextchile!=r用于防环
			else
			{
				p = S.top();
				S.pop();
				this->visit(p);
				pre= p;
				p = NULL;//这一点不容易想到,比较容易直接给它设为指向栈顶元素，还容易不断地重复逻辑判断，流程控制较复杂

			}

		}
	}

}


Treenode& Bitree::setroot(Treenode* a)
{
	
	this->root = a;
	return *this->root;
}
void Bitree::visit(Treenode*a)
{
	if (a->val != '#')
	{
		cout << a->val;
		this->count++;
	}

}

"源文件.cpp":

#define _CRT_SECURE_NO_WARNINGS 1

#include	"tree.hpp"



int main()
{
	

	//先创建空树再遍历赋值
	Bitree T;
	Treenode m1('A');
	Treenode m2('B');
	Treenode m3('C');
	Treenode m4('D');
	Treenode m5('E');
	Treenode m6('F');
	Treenode m7('G');

	T.setroot(&m1);
	m1.setfirstchild(&m2);
	m1.setnextchild(&m3);

	m2.setfirstchild(&m4); 
	m2.setnextchild(&m5);
	m3.setfirstchild(&m6);
	m3.setrtag(true) ;
	m4.setnextchild(&m7);
	//cout << m4.getnextchild().getval();
	m4.setrtag(true);
	m5.setrtag(true);
	m5.setrtag(true);
	m6.setrtag(true);
	m6.setrtag(true);
	m7.setrtag(true);
	m7.setrtag(true) ;


	cout << "后序遍历序列为：";
	T.postorder_nonrecursion_traversal();
	cout << endl;
	cout << "树中结点数为：" << T.getcount() << endl;
	
	



	system("pause");
	return 0;
}

代码测试：

数据结构与算法学习：二叉树的后序遍历的递归与非递归实现，以及非递归实现中的流程控制的说明。文章来源地址https://www.toymoban.com/news/detail-421539.html