1 数组
设数组元素长度为 L。
1.1 一维数组
数组下标从 0 开始(A[0]–A[n],一共 n+1 个),假设当前下标为A[i]:
第几个 = i + 1存储地址 = 首地址 + (第几个-1) * L = A[0] 地址 + i * L
数组下标从 1 开始(A[1]–A[n],一共 n 个),假设当前下标为A[i]:
第几个 = i存储地址 = 首地址 + (第几个-1) * L = A[1] 地址 + (i - 1) * L
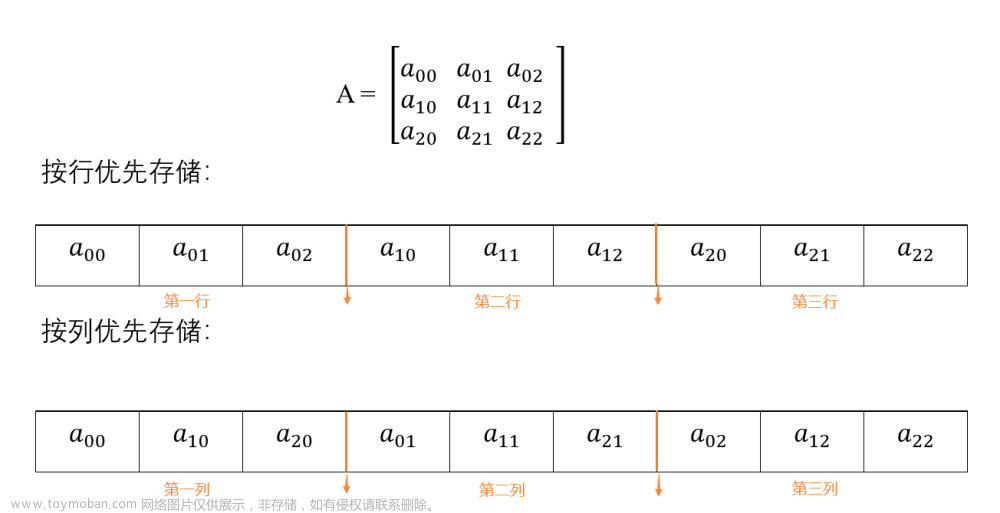
1.2 二维数组
数组下标从 0 开始(A[0, 0]–A[a, b],每行 a+1 个,每列 b+1 个),行优先,假设当前下标为A[i, j]:
第几个 = i * (a+1) + j + 1存储地址 = 首地址 + (第几个-1) * L = A[0, 0] 地址 + (i * (a+1) + j) * L
数组下标从 0 开始(A[0, 0]–A[a, b],每行 a+1 个,每列 b+1 个),列优先,假设当前下标为A[i, j]:
第几个 = j * (b+1) + i + 1存储地址 = 首地址 + (第几个-1) * L = A[0, 0] 地址 + (j * (b+1) + i) * L
数组下标从 1 开始(A[1, 1]–A[a, b],每行 a 个,每列 b 个),行优先,假设当前下标为A[i, j]:
第几个 = (i-1) * a + j存储地址 = 首地址 + (第几个-1) * L = A[1, 1] 地址 + ((i-1) * a + j - 1) * L
数组下标从 1 开始(A[1, 1]–A[a, b],每行 a 个,每列 b 个),列优先,假设当前下标为A[i, j]:
第几个 = (j-1) * b + i存储地址 = 首地址 + (第几个-1) * L = A[1, 1] 地址 + ((j-1) * b + i - 1) * L
2 对称矩阵
设矩阵 Aaxb,一般情况下,矩阵为方阵,即 a = b = n。设数组元素长度为 L,一般推导思路是从“求矩阵元素是数组的第几个元素”入手,进而推出数组元素的下标。
2.1 上三角部分(i ≤ j)
矩阵下标从 0 开始(A[0, 0]–A[a, b],每行 a+1 个,每列 b+1 个),行优先,假设当前下标为A[i, j]:
数组的第几个元素 = a + (a-1) + (a-2) +…+ (a-i+2) + (j-i+1) = (i-1)(2a-i+2)/2 + (j-i+1)存储地址 = 首地址 + (第几个-1) * L = 数组首地址 + ((i-1)(2a-i+2)/2 + (j-i)) * L
矩阵下标从 0 开始(A[0, 0]–A[a, b],每行 a+1 个,每列 b+1 个),列优先,假设当前下标为A[i, j]:
数组的第几个元素 = 1 + 2 + 3 +…+ j + (i+1) = j(j+1)/2 + (i+1)存储地址 = 首地址 + (第几个-1) * L = 数组首地址 + (j(j+1)/2 + i) * L
矩阵下标从 1 开始(A[1, 1]–A[a, b],每行 a 个,每列 b 个),行优先,假设当前下标为A[i, j]:
数组的第几个元素 = a + (a-1) + (a-2) +…+ (a-i+1) + (j-i+1) = i(2a-i+1)/2 + (j-i+1)存储地址 = 首地址 + (第几个-1) * L = 数组首地址 + (i(2a-i+1)/2 + (j-i)) * L
矩阵下标从 1 开始(A[1, 1]–A[a, b],每行 a 个,每列 b 个),列优先,假设当前下标为A[i, j]:
数组的第几个元素 = 1 + 2 + 3 +…+ (j-1) + i = j(j-1)/2 + i存储地址 = 首地址 + (第几个-1) * L = 数组首地址 + (j(j-1)/2 + i - 1) * L
2.2 下三角部分(i ≥ j)
矩阵下标从 0 开始(A[0, 0]–A[a, b],每行 a+1 个,每列 b+1 个),行优先,假设当前下标为A[i, j]:
数组的第几个元素 = 1 + 2 + 3 +…+ i + (j+1) = i(i+1)/2 + (j+1)存储地址 = 首地址 + (第几个-1) * L = 数组首地址 + (i(i+1)/2 + j) * L
矩阵下标从 0 开始(A[0, 0]–A[a, b],每行 a+1 个,每列 b+1 个),列优先,假设当前下标为A[i, j]:
数组的第几个元素 = b + (b-1) + (b-2) +…+ (b-j+2) + (i-j+1) = (j-1)(2b-j+2)/2 + (i-j+1)存储地址 = 首地址 + (第几个-1) * L = 数组首地址 + ((j-1)(2b-j+2)/2 + (i-j)) * L
矩阵下标从 1 开始(A[1, 1]–A[a, b],每行 a 个,每列 b 个),行优先,假设当前下标为A[i, j]:
数组的第几个元素 = 1 + 2 + 3 +…+ (i-1) + j = i(i-1)/2 + j存储地址 = 首地址 + (第几个-1) * L = 数组首地址 + (i(i-1)/2 + j - 1) * L
矩阵下标从 1 开始(A[1, 1]–A[a, b],每行 a 个,每列 b 个),列优先,假设当前下标为A[i, j]:
数组的第几个元素 = b + (b-1) + (b-2) +…+ (b-j+1) + (i-j+1) = j(2b-j+1)/2 + (i-j+1)存储地址 = 首地址 + (第几个-1) * L = 数组首地址 + (j(2b-j+1)/2 + (i-j)) * L
3 三角矩阵
设矩阵 Aaxb,一般情况下,矩阵为方阵,即 a = b = n。设数组元素长度为 L。推导过程与对称矩阵相同。
3.1 上三角矩阵(i ≤ j 的元素不全为 0)
(1)当 i ≤ j 时(不全为 0):
矩阵下标从 0 开始(A[0, 0]–A[a, b],每行 a+1 个,每列 b+1 个),行优先,假设当前下标为A[i, j]:
数组的第几个元素 = a + (a-1) + (a-2) +…+ (a-i+2) + (j-i+1) = (i-1)(2a-i+2)/2 + (j-i+1)存储地址 = 首地址 + (第几个-1) * L = 数组首地址 + ((i-1)(2a-i+2)/2 + (j-i)) * L
矩阵下标从 0 开始(A[0, 0]–A[a, b],每行 a+1 个,每列 b+1 个),列优先,假设当前下标为A[i, j]:
数组的第几个元素 = 1 + 2 + 3 +…+ j + i + 1 = j(j+1)/2 + i + 1存储地址 = 首地址 + (第几个-1) * L = 数组首地址 + (j(j+1)/2 + i) * L
矩阵下标从 1 开始(A[1, 1]–A[a, b],每行 a 个,每列 b 个),行优先,假设当前下标为A[i, j]:
数组的第几个元素 = a + (a-1) + (a-2) +…+ (a-i+1) + (j-i+1) = i(2a-i+1)/2 + (j-i+1)存储地址 = 首地址 + (第几个-1) * L = 数组首地址 + (i(2a-i+1)/2 + (j-i)) * L
矩阵下标从 1 开始(A[1, 1]–A[a, b],每行 a 个,每列 b 个),列优先,假设当前下标为A[i, j]:
数组的第几个元素 = 1 + 2 + 3 +…+ (j-1) + i = j(j-1)/2 + i存储地址 = 首地址 + (第几个-1) * L = 数组首地址 + (j(j-1)/2 + i - 1) * L
(2)当 i > j 时(全为 0):
矩阵下标从 0 开始(A[0, 0]–A[a, b],每行 a+1 个,每列 b+1 个),假设当前下标为A[i, j]:
数组的第几个元素 = n(n+1)/2 + 1
矩阵下标从 1 开始(A[0, 0]–A[a, b],每行 a 个,每列 b 个),假设当前下标为A[i, j]:
数组的第几个元素 = n(n-1)/2 + 1
3.2 下三角矩阵(i ≥ j 的元素不全为 0)
(1)当 i ≥ j 时(不全为 0):
矩阵下标从 0 开始(A[0, 0]–A[a, b],每行 a+1 个,每列 b+1 个),行优先,假设当前下标为A[i, j]:
数组的第几个元素 = 1 + 2 + 3 +…+ i + j = i(i+1)/2 + j + 1存储地址 = 首地址 + (第几个-1) * L = 数组首地址 + (i(i+1)/2 + j) * L
矩阵下标从 0 开始(A[0, 0]–A[a, b],每行 a+1 个,每列 b+1 个),列优先,假设当前下标为A[i, j]:
数组的第几个元素 = b + (b-1) + (b-2) +…+ (b-j+2) + (i-j+1) = (j-1)(2b-j+2)/2 + (i-j+1)存储地址 = 首地址 + (第几个-1) * L = 数组首地址 + ((j-1)(2b-j+2)/2 + (i-j)) * L
矩阵下标从 1 开始(A[1, 1]–A[a, b],每行 a 个,每列 b 个),行优先,假设当前下标为A[i, j]:
数组的第几个元素 = 1 + 2 + 3 +…+ (i-1) + j = i(i-1)/2 + j存储地址 = 首地址 + (第几个-1) * L = 数组首地址 + (i(i-1)/2 + j - 1) * L
矩阵下标从 1 开始(A[1, 1]–A[a, b],每行 a 个,每列 b 个),列优先,假设当前下标为A[i, j]:
数组的第几个元素 = b + (b-1) + (b-2) +…+ (b-j+1) + (i-j+1) = j(2b-j+1)/2 + (i-j+1)存储地址 = 首地址 + (第几个-1) * L = 数组首地址 + (j(2b-j+1)/2 + (i-j)) * L
(2)当 i < j 时(全为 0):
矩阵下标从 0 开始(A[0, 0]–A[a, b],每行 a+1 个,每列 b+1 个),假设当前下标为A[i, j]:
数组的第几个元素 = n(n+1)/2 + 1
矩阵下标从 1 开始(A[0, 0]–A[a, b],每行 a 个,每列 b 个),假设当前下标为A[i, j]:
数组的第几个元素 = n(n-1)/2 + 1
4 三对角矩阵
设矩阵 Aaxb,一般情况下,矩阵为方阵,即 a = b = n。设数组元素长度为 L。
矩阵下标从 0 开始(A[0, 0]–A[a, b],每行 a+1 个,每列 b+1 个),行优先,假设当前下标为A[i, j]:
- 第 1 ~ i 行有几个元素:
3i-1;A[i, j] 是第 i+1 行第 j-i+2 个元素 数组的第几个元素 = (3i-1) + (j-i+2) = 2 * i + j + 1存储地址 = 首地址 + (第几个-1) * L = 数组首地址 + (2 * i + j) * L
矩阵下标从 0 开始(A[0, 0]–A[a, b],每行 a+1 个,每列 b+1 个),列优先,假设当前下标为A[i, j]:
- 第 1 ~ j 列有几个元素:
3j-1;A[i, j] 是第 j+1 行第 i-j+2 个元素 数组的第几个元素 = (3j-1) + (i-j+2) = 2 * j + i + 1存储地址 = 首地址 + (第几个-1) * L = 数组首地址 + (2 * j + i) * L
矩阵下标从 1 开始(A[1, 1]–A[a, b],每行 a 个,每列 b 个),行优先,假设当前下标为A[i, j]:
- 第 1 ~ i-1 行有几个元素:
3(i-1)-1;A[i, j] 是第 i 行第 j-i+2 个元素 数组的第几个元素 = 3(i-1)-1 + (j-i+2) = 2 * (i-1) + j存储地址 = 首地址 + (第几个-1) * L = 数组首地址 + (2 * (i-1) + j - 1) * L
矩阵下标从 1 开始(A[1, 1]–A[a, b],每行 a 个,每列 b 个),列优先,假设当前下标为A[i, j]:
- 第 1 ~ j-1 列有几个元素:
3(j-1)-1;A[i, j] 是第 j 列第 i-j+2 个元素 数组的第几个元素 = 3(j-1)-1 + (i-j+2) = 2 * (j-1) + i存储地址 = 首地址 + (第几个-1) * L = 数组首地址 + (2 * (j-1) + i - 1) * L
【注】以上公式均不适用于第一行。文章来源:https://www.toymoban.com/news/detail-421586.html
5 稀疏矩阵
三元组、十字链表法。文章来源地址https://www.toymoban.com/news/detail-421586.html
到了这里,关于【数据结构-矩阵】矩阵的相关公式推导的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!