【算法】灰狼算法GWO优化支持向量机回归SVR模型-Toy模板网

这篇具有很好参考价值的文章主要介绍了【算法】灰狼算法GWO优化支持向量机回归SVR模型。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

灰狼算法GWO

GWO是一种基于灰狼行为的优化算法，由Mirjalili等人于2014年提出。该算法模拟灰狼群的捕猎行为，通过模拟狼群中的Alpha、Beta、Delta三种角色的行为来实现全局优化，具有收敛速度快、精度高、易于实现等特点。

GWO算法的基本流程

初始化狼群位置和适应度函数。
计算每个狼的适应度，并记录Alpha、Beta、Delta狼的位置。
根据Alpha、Beta、Delta狼的位置更新狼群位置。
重复步骤2和3，直到达到预设的停止条件。

在更新狼群位置时，GWO算法采用了三种不同的策略：

狼群中的Alpha狼对其他狼施加影响，使它们朝向Alpha狼的位置移动。
狼群中的Beta狼对其他狼施加影响，使它们朝向Beta狼的位置移动。
狼群中的Delta狼对其他狼施加影响，使它们朝向Delta狼的位置移动。

通过这些策略，GWO算法能够在搜索空间中快速地找到全局最优解。

优点

相对简单
灰狼算法的原理比较简单，易于理解和实现。
全局搜索能力强
灰狼算法在全局搜索中表现较好，能够有效地探索搜索空间，找到全局最优解。
收敛速度快
灰狼算法能够快速收敛到最优解，具有较高的收敛速度

缺点

参数设置困难
灰狼算法的性能受到参数设置的影响较大，不同的问题可能需要不同的参数设置，参数设置困难。
对问题的依赖性较强
灰狼算法对问题的依赖性较强，对于复杂的多模态问题或非线性问题，可能无法取得很好的效果。
可能陷入局部最优
灰狼算法在局部搜索能力上相对较弱，可能会陷入局部最优解而无法达到全局最优解。

总得来说，GWO算法是一种高效的全局优化算法，可以应用于多种优化问题中。

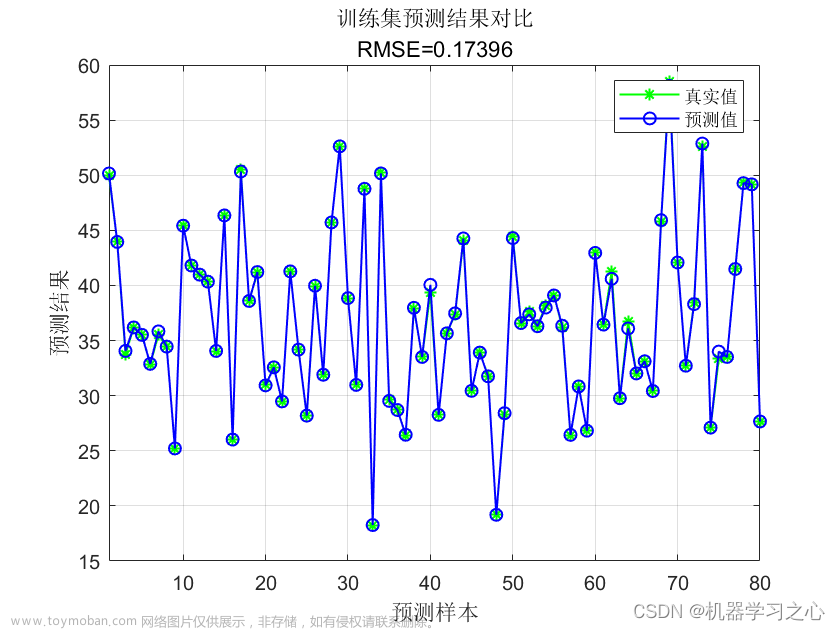
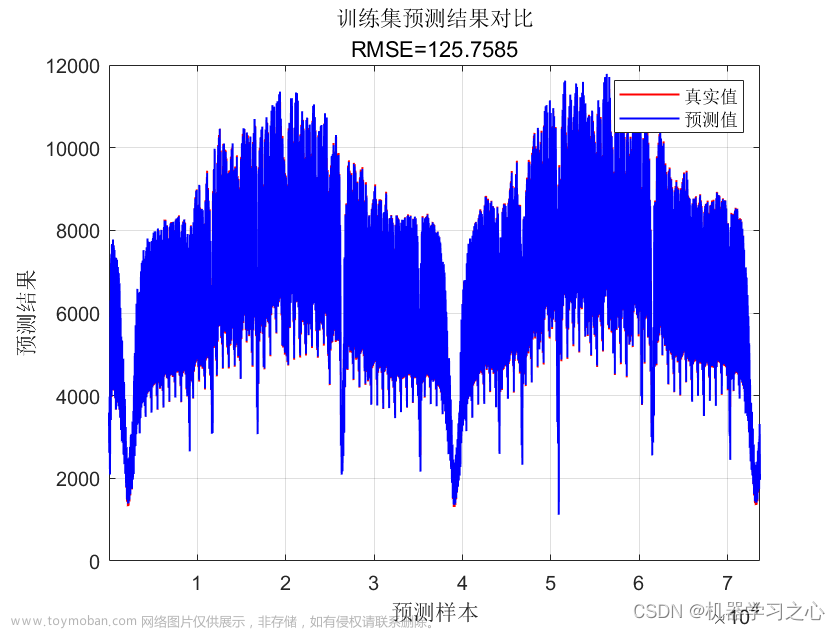
实例模型，6输入1输出

在本次实例模型中，数据集采用6输入1输出。针对其他的输入特征值数量，该模型依旧适用。

数据集导入

X_train = np.array([[1, 2,3,4,5,6], [2, 4 ,3,4,5,6], [3, 6 ,7,8,9,10], [4, 8,11,12,3,1], [5, 10,2,3,2,3]])
y_train = np.array([3, 6, 9, 12, 15])

该部分数据集导入的方法各异，可以采用excel、mat等各种形式。
本示例模型中训练集和测试集没有进行划分，采用同一组数据集，如有需要，可以进行自定义添加。

定义适应度函数

def fitness_func(position):
    #防止valueError
    if position[1]<=0:
        position[1] =0.0001
    if position[0]<=0:
        position[0] = 0.0001
    svm.set_params(C=position[0], gamma=position[1])
    svm.fit(X_train, y_train)
    y_pred = svm.predict(X_train)
    mse = np.mean((y_train - y_pred) ** 2)
    fitness = 1 / (mse + 1e-6)
    return fitness

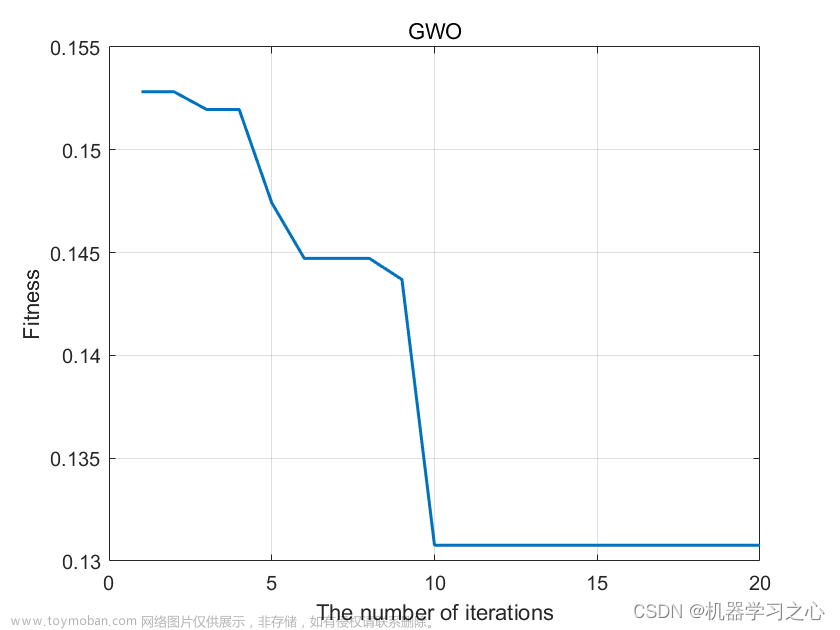
GWO优化

gwo = GWO(fitness_func, 2, lb=[0.1, 0.01], ub=[100, 10], N=N, Max_iter=Max_iter)
gwo.optimize()

GWO类在完整模型代码中有提供，已经封装完成文章来源地址https://www.toymoban.com/news/detail-421788.html

训练最佳SVR模型

svm.set_params(C=gwo.best_pos[0], gamma=gwo.best_pos[1])
svm.fit(X_train, y_train)
y_pred = svm.predict(X_train)
mse = np.mean((y_train - y_pred) ** 2)

此时的超参数C和gamma已经为训练好的数值

完整模型代码

demo.py

import numpy as np
from sklearn.svm import SVR
from gwo import GWO

# 训练数据
X_train = np.array([[1, 2,3,4,5,6], [2, 4 ,3,4,5,6], [3, 6 ,7,8,9,10], [4, 8,11,12,3,1], [5, 10,2,3,2,3]])
y_train = np.array([3, 6, 9, 12, 15])

# GWO参数
N = 5  # 狼群数量
Max_iter = 100  # 最大迭代次数

# 定义SVR模型
svm = SVR(kernel='rbf', C=1, gamma=0.1)

# 定义适应度函数
def fitness_func(position):
    #防止valueError
    if position[1]<=0:
        position[1] =0.0001
    if position[0]<=0:
        position[0] = 0.0001
    svm.set_params(C=position[0], gamma=position[1])
    svm.fit(X_train, y_train)
    y_pred = svm.predict(X_train)
    mse = np.mean((y_train - y_pred) ** 2)
    fitness = 1 / (mse + 1e-6)
    return fitness

# GWO优化
gwo = GWO(fitness_func, 2, lb=[0.1, 0.01], ub=[100, 10], N=N, Max_iter=Max_iter)
gwo.optimize()

# 训练最佳SVR模型
svm.set_params(C=gwo.best_pos[0], gamma=gwo.best_pos[1])
svm.fit(X_train, y_train)
y_pred = svm.predict(X_train)
mse = np.mean((y_train - y_pred) ** 2)

# 输出结果
print('最小均方误差：', mse)
print('最佳参数：', gwo.best_pos)

gwo.py

import numpy as np

class GWO:
    def __init__(self, fitness_func, dim, lb, ub, N, Max_iter):
        self.fitness_func = fitness_func  # 适应度函数
        self.dim = dim  # 变量维度
        self.lb = lb  # 变量下限
        self.ub = ub  # 变量上限
        self.N = N  # 狼群数量
        self.Max_iter = Max_iter  # 最大迭代次数

    def optimize(self):
        # 初始化狼群位置
        X = np.random.uniform(self.lb, self.ub, (self.N, self.dim))
        alpha_pos = np.zeros(self.dim)
        beta_pos = np.zeros(self.dim)
        delta_pos = np.zeros(self.dim)
        alpha_fit = float('-inf')
        beta_fit = float('-inf')
        delta_fit = float('-inf')

        # 迭代优化
        for t in range(self.Max_iter):
            for i in range(self.N):
                # 计算适应度
                fitness = self.fitness_func(X[i])
                if fitness > alpha_fit:
                    alpha_fit = fitness
                    alpha_pos = X[i].copy()
                elif fitness > beta_fit:
                    beta_fit = fitness
                    beta_pos = X[i].copy()
                elif fitness > delta_fit:
                    delta_fit = fitness
                    delta_pos = X[i].copy()

            # 更新狼群位置
            a = 2 - 2 * t / self.Max_iter
            for i in range(self.N):
                r1 = np.random.rand(self.dim)
                r2 = np.random.rand(self.dim)
                A = 2 * a * r1 - a
                C = 2 * r2
                D_alpha = np.abs(C * alpha_pos - X[i])
                X1 = alpha_pos - A * D_alpha
                r1 = np.random.rand(self.dim)
                r2 = np.random.rand(self.dim)
                A = 2 * a * r1 - a
                C = 2 * r2
                D_beta = np.abs(C * beta_pos - X[i])
                X2 = beta_pos - A * D_beta
                r1 = np.random.rand(self.dim)
                r2 = np.random.rand(self.dim)
                A = 2 * a * r1 - a
                C = 2 * r2
                D_delta = np.abs(C * delta_pos - X[i])
                X3 = delta_pos - A * D_delta
                X[i] = (X1 + X2 + X3) / 3

        # 记录最佳位置
        self.best_pos = alpha_pos