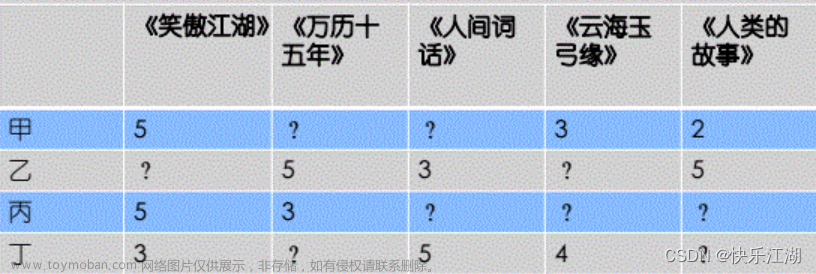
定义1 给定连续函数
f
(
x
)
f(x)
f(x),
x
∈
Ω
⊆
R
x\in\Omega\subseteq\text{ℝ}
x∈Ω⊆R。设
x
,
x
1
∈
Ω
x,x_1\in\Omega
x,x1∈Ω,
Δ
x
=
x
−
x
1
\Delta x=x-x_1
Δx=x−x1
称为变量
x
x
x的差分。此时,
x
=
x
1
+
Δ
x
x=x_1+\Delta x
x=x1+Δx。称
f
(
x
1
+
Δ
x
)
−
f
(
x
1
)
Δ
x
\frac{f(x_1+\Delta x)-f(x_1)}{\Delta x}
Δxf(x1+Δx)−f(x1)
为
f
(
x
)
f(x)
f(x)在
x
1
x_1
x1处的前向差分。称
f
(
x
1
)
−
f
(
x
1
−
Δ
x
)
Δ
x
\frac{f(x_1)-f(x_1-\Delta x)}{\Delta x}
Δxf(x1)−f(x1−Δx)
为
f
(
x
)
f(x)
f(x)在
x
1
x_1
x1处的后向差分。称
f
(
x
1
+
Δ
x
/
2
)
−
f
(
x
1
−
Δ
x
/
2
)
Δ
x
\frac{f(x_1+\Delta x/2)-f(x_1-\Delta x/2)}{\Delta x}
Δxf(x1+Δx/2)−f(x1−Δx/2)
为
f
(
x
)
f(x)
f(x)在
x
1
x_1
x1处的中心差分。
若函数
f
(
x
)
f(x)
f(x)在
x
1
x_1
x1处可微,则
f
(
x
)
f(x)
f(x)在
x
1
x_1
x1处的导数为
f
′
(
x
1
)
=
lim
Δ
x
→
0
f
(
x
)
−
f
(
x
1
)
Δ
x
=
lim
Δ
x
→
0
f
(
x
1
+
Δ
x
)
−
f
(
x
1
)
Δ
x
f'(x_1)=\lim_{\Delta x\rightarrow0}\frac{f(x)-f(x_1)}{\Delta x}=\lim_{\Delta x\rightarrow0}\frac{f(x_1+\Delta x)-f(x_1)}{\Delta x}
f′(x1)=Δx→0limΔxf(x)−f(x1)=Δx→0limΔxf(x1+Δx)−f(x1)
即
f
(
x
)
f(x)
f(x)在
x
1
x_1
x1处的导数
f
′
(
x
1
)
f'(x_1)
f′(x1)是
f
(
x
)
f(x)
f(x)在
x
1
x_1
x1处的前向差分
f
(
x
1
+
Δ
x
)
−
f
(
x
1
)
Δ
x
\frac{f(x_1+\Delta x)-f(x_1)}{\Delta x}
Δxf(x1+Δx)−f(x1)当
x
x
x的差分
Δ
x
\Delta x
Δx趋于0时的极限。因此,当
∣
Δ
x
∣
|\Delta x|
∣Δx∣充分小时,
f
′
(
x
1
)
≈
f
(
x
1
)
−
f
(
x
1
−
Δ
x
)
Δ
x
.
f'(x_1)\approx \frac{f(x_1)-f(x_1-\Delta x)}{\Delta x}.
f′(x1)≈Δxf(x1)−f(x1−Δx).
在
f
(
x
)
f(x)
f(x)在
x
1
x_1
x1处的后向差分
f
(
x
1
)
−
f
(
x
1
−
Δ
x
)
Δ
x
\frac{f(x_1)-f(x_1-\Delta x)}{\Delta x}
Δxf(x1)−f(x1−Δx)中对变量差分
Δ
x
\Delta x
Δx作变换
Δ
x
′
=
−
Δ
x
\Delta x'=-\Delta x
Δx′=−Δx,得
f
(
x
1
)
−
f
(
x
1
−
Δ
x
)
Δ
x
=
f
(
x
1
)
−
f
(
x
1
+
Δ
′
x
)
−
Δ
x
′
=
f
(
x
1
+
Δ
x
′
)
−
f
(
x
1
)
Δ
x
′
\frac{f(x_1)-f(x_1-\Delta x)}{\Delta x}=\frac{f(x_1)-f(x_1+\Delta'x)}{-\Delta x'}=\frac{f(x_1+\Delta x')-f(x_1)}{\Delta x'}
Δxf(x1)−f(x1−Δx)=−Δx′f(x1)−f(x1+Δ′x)=Δx′f(x1+Δx′)−f(x1)
由于
Δ
x
′
→
0
\Delta x'\rightarrow0
Δx′→0当且进当
Δ
x
→
0
\Delta x\rightarrow0
Δx→0,故当
∣
Δ
x
∣
|\Delta x|
∣Δx∣充分小时,有
f
′
(
x
1
)
≈
f
(
x
1
)
−
f
(
x
1
−
Δ
x
)
Δ
x
.
f'(x_1)\approx\frac{f(x_1)-f(x_1-\Delta x)}{\Delta x}.
f′(x1)≈Δxf(x1)−f(x1−Δx).
对于
f
(
x
)
f(x)
f(x)在
x
1
x_1
x1处的中心差分
f
(
x
1
+
Δ
x
/
2
)
−
f
(
x
1
−
Δ
x
/
2
)
Δ
x
=
f
(
x
1
+
Δ
x
/
2
)
−
f
(
x
1
)
+
f
(
x
1
)
−
f
(
x
1
−
Δ
x
/
2
)
Δ
x
=
1
2
f
(
x
1
+
Δ
x
/
2
)
−
f
(
x
1
)
+
f
(
x
1
)
−
f
(
x
1
−
Δ
x
/
2
)
Δ
x
/
2
=
1
2
[
f
(
x
1
+
Δ
x
/
2
)
−
f
(
x
1
)
Δ
x
/
2
+
f
(
x
1
)
−
f
(
x
1
−
Δ
x
/
2
)
Δ
x
/
2
]
\frac{f(x_1+\Delta x/2)-f(x_1-\Delta x/2)}{\Delta x}=\frac{f(x_1+\Delta x/2)-f(x_1)+f(x_1)-f(x_1-\Delta x/2)}{\Delta x}\\ =\frac{1}{2}\frac{f(x_1+\Delta x/2)-f(x_1)+f(x_1)-f(x_1-\Delta x/2)}{\Delta x/2}\\ =\frac{1}{2}\left[\frac{f(x_1+\Delta x/2)-f(x_1)}{\Delta x/2}+\frac{f(x_1)-f(x_1-\Delta x/2)}{\Delta x/2}\right]
Δxf(x1+Δx/2)−f(x1−Δx/2)=Δxf(x1+Δx/2)−f(x1)+f(x1)−f(x1−Δx/2)=21Δx/2f(x1+Δx/2)−f(x1)+f(x1)−f(x1−Δx/2)=21[Δx/2f(x1+Δx/2)−f(x1)+Δx/2f(x1)−f(x1−Δx/2)]
所以
f
′
(
x
1
)
≈
f
(
x
1
+
Δ
x
/
2
)
−
f
(
x
1
−
Δ
x
/
2
)
Δ
x
.
f'(x_1)\approx\frac{f(x_1+\Delta x/2)-f(x_1-\Delta x/2)}{\Delta x}.
f′(x1)≈Δxf(x1+Δx/2)−f(x1−Δx/2).
令
g
(
x
)
=
f
(
x
+
Δ
x
/
2
)
−
f
(
x
−
Δ
x
/
2
)
Δ
x
g(x)=\frac{f(x+\Delta x/2)-f(x-\Delta x/2)}{\Delta x}
g(x)=Δxf(x+Δx/2)−f(x−Δx/2)
称其为
f
(
x
)
f(x)
f(x)的广义导数。对
f
(
x
)
f(x)
f(x)的广义导数
g
(
x
)
g(x)
g(x)计算其在
x
1
x_1
x1处的中心差分,可得
f
(
x
)
f(x)
f(x)在
x
1
x_1
x1处的二阶导数近似计算公式
f
′
′
(
x
1
)
≈
f
(
x
1
+
Δ
x
)
+
f
(
x
1
−
Δ
x
)
−
2
f
(
x
1
)
Δ
x
2
.
f''(x_1)\approx\frac{f(x_1+\Delta x)+f(x_1-\Delta x)-2f(x_1)}{\Delta x^2}.
f′′(x1)≈Δx2f(x1+Δx)+f(x1−Δx)−2f(x1).
利用
f
′
(
x
1
)
f'(x_1)
f′(x1)和
f
"
(
x
1
)
f"(x_1)
f"(x1)的近似公式,实现一元函数二阶可微的一、二阶导数计算的Python函数定义如下
def der_scalar(f,x1): #f表示函数,x1表示自变量值
dx=1e-7 #设置Δx=0.0000001
f1=(f(x1+dx/2)-f(x1-dx/2))/dx #计算一阶导数
f2=(f(x1+dx)+f(x1-dx)-2*f(x1))/dx**2 #计算二阶导数
return f1,f2
程序中第1~5定义函数der_scalar。两个参数之一f表示二阶可微函数
f
(
x
)
f(x)
f(x),x1表示自变量值
x
1
x_1
x1。第2行设置自变量增量
Δ
x
=
1
0
−
7
\Delta x=10^{-7}
Δx=10−7为dx。第3行按
f
′
(
x
1
)
f'(x_1)
f′(x1)的中心差分近似式计算
x
1
x_1
x1处的一阶导数
f
′
(
x
1
)
f'(x_1)
f′(x1)为f1。第4行按广义导数的中心差分计算
x
1
x_1
x1处的二阶导数
f
′
′
(
x
1
)
f''(x_1)
f′′(x1)为f2。
例1 考虑函数
f
(
x
)
=
sin
x
2
f(x)=\sin{x^2}
f(x)=sinx2,其一阶导数
f
′
(
x
)
=
2
x
cos
x
2
f'(x)=2x\cos{x^2}
f′(x)=2xcosx2,二阶导数
f
′
′
(
x
)
=
2
(
cos
x
2
−
2
x
2
sin
x
2
)
f''(x)=2(\cos{x^2}-2x^2\sin{x^2})
f′′(x)=2(cosx2−2x2sinx2)。故对
x
1
=
π
3
x_1=\frac{\pi}{3}
x1=3π可算得
f
′
(
x
1
)
=
0.9563
f'(x_1)=0.9563
f′(x1)=0.9563,
f
′
′
(
x
1
)
=
−
2.9893
f''(x_1)=-2.9893
f′′(x1)=−2.9893。下列代码比较直接由导函数解析式计算和调用上列程序定义的der_scalar函数计算的结果。
import numpy as np #导入numpy
f=lambda x:np.sin(x**2) #设置函数f(x)
f1=lambda x:2*x*np.cos(x**2) #设置一阶导数f'(x)
f2=lambda x:2*(np.cos(x**2)-2*np.sin(x**2)*x**2) #设置二阶导数f"(x)
x1=np.pi/3 #设置自变量x1
print((f1(x1),f2(x1))) #解析计算
print(der_scalar(f,x1)) #数值计算
程序的2、3、4行分别设置 f ( x ) f(x) f(x)、 f ′ ( x ) f'(x) f′(x)和 f ′ ′ ( x ) f''(x) f′′(x)的解析式。第5行设置自变量的值 x 1 = π 3 x_1=\frac{\pi}{3} x1=3π。第6行输出解析计算结果,第7行调用der_scalar函数数值地计算 f ′ ( x 1 ) f'(x_1) f′(x1)和 f ′ ′ ( x 1 ) f''(x_1) f′′(x1)。运行程序,输出
(0.9563079109495481, -2.9893240816612874)
(0.9563079098976839, -3.0000693287648676)
输出的第1行为解析计算的结果,第2行为数值计算结果。比较两者可见der_scalar函数计算的一阶导数结果精度是很高的,二阶导数的计算精度稍差。这是因为,这是对“广义导数”进行差分计算的结果。换句话说,在计算二阶导数时,累积了两次计算误差,产生了误差的“放大”效应。尽管如此,der_scalar函数在大多数场合都能满足应用的要求。
例2: 下图给出了移动无线通信系统的简化模型。有两个同为
1
1
1个高度单位相矩
2
2
2个长度单位的相邻基站,手机用户所处位置为
x
x
x,手机收到的基站信号的功率与用户与基站之间的距离平方成反比。试确定用户最为合适的位置,使得信号干扰比最大,即用户接收到来自基站
1
1
1的信号功率与来自基站
2
2
2的信号功率之间的比值最大。
解:按题意,手机收到的基站信号的功率与用户与基站之间的距离平方成反比。即收到基站1和基站2的功率分别为
w
1
=
1
1
+
x
2
w
2
=
1
1
+
(
2
−
x
)
2
\begin{array}{l} w_1=\frac{1}{1+x^2}\\ w_2=\frac{1}{1+(2-x)^2} \end{array}
w1=1+x21w2=1+(2−x)21
为使得信号干扰比最大,即用户接收到来自基站1的信号功率与来自基站2的信号功率之间的比值最大,求函数
f
(
x
)
=
w
1
w
2
=
1
+
(
2
−
x
)
2
1
+
x
2
f(x)=\frac{w_1}{w_2}=\frac{1+(2-x)^2}{1+x^2}
f(x)=w2w1=1+x21+(2−x)2的最大值点
x
0
x_0
x0。
由于
f
(
x
)
f(x)
f(x)二阶连续可微,为计算
f
(
x
)
f(x)
f(x)的最大值点,先求得
f
(
x
)
f(x)
f(x)驻点。
f
′
(
x
)
=
−
2
(
2
−
x
)
(
1
+
x
2
)
−
2
x
(
1
+
(
2
−
x
)
2
)
(
1
+
x
2
)
2
=
4
(
x
2
−
2
x
−
1
)
(
1
+
x
2
)
2
=
4
(
(
x
−
1
)
2
−
2
)
(
1
+
x
2
)
2
=
4
(
(
x
−
1
−
2
)
(
x
−
1
+
2
)
)
(
1
+
x
2
)
2
f'(x)=\frac{-2(2-x)(1+x^2)-2x(1+(2-x)^2)}{(1+x^2)^2}\\ =\frac{4(x^2-2x-1)}{(1+x^2)^2}=\frac{4((x-1)^2-2)}{(1+x^2)^2}\\ =\frac{4((x-1-\sqrt{2})(x-1+\sqrt{2}))}{(1+x^2)^2}
f′(x)=(1+x2)2−2(2−x)(1+x2)−2x(1+(2−x)2)=(1+x2)24(x2−2x−1)=(1+x2)24((x−1)2−2)=(1+x2)24((x−1−2)(x−1+2))
令
f
′
(
x
)
=
0
f'(x)=0
f′(x)=0,即得驻点
x
1
=
1
−
2
x_1=1-\sqrt{2}
x1=1−2和
x
2
=
1
+
2
x_2=1+\sqrt{2}
x2=1+2。按二阶可微函数极值点的必要条件,需计算
f
(
x
)
f(x)
f(x)的二阶导数
f
′
′
(
x
)
f''(x)
f′′(x)在驻点处的值,通过二阶导数值的正负以判断是极大值点或是极小值点。下列代码完成计算过程。
import numpy as np #导入numpy
f=lambda x:(1+(2-x)**2)/(1+x**2) #设置函数f(x)
x1=1-np.sqrt(2) #驻点x1
x2=1+np.sqrt(2) #驻点x2
print('%.1f,%.4f'%der_scalar(f,x1)) #计算x1处一、二阶导数
print('%.1f,%.4f'%der_scalar(f,x2)) #计算x2处一、二阶导数
利用代码中的注释信息不难理解程序。仅提请注意第3、4行分别设置的是驻点 x 1 = 1 − 2 x_1=1-\sqrt{2} x1=1−2和 x 2 = 1 + 2 x_2=1+\sqrt{2} x2=1+2。运行程序,输出:文章来源:https://www.toymoban.com/news/detail-421892.html
0.0,-8.2107
0.0,0.2566
第1行输出的是 f ( x ) f(x) f(x)在 x 1 = 1 − 2 x_1=1-\sqrt{2} x1=1−2处的一、二阶导数值,说明 x 1 x_1 x1确实为驻点,且由于在 x 1 x_1 x1处的二阶导数值近似为-8.2107,根据极值点的充分条件知 x 1 x_1 x1为 f ( x ) f(x) f(x)的唯一极大值点,即为本题所求。第二行的输出表明 x 2 = 1 + 2 x_2=1+\sqrt{2} x2=1+2是 f ( x ) f(x) f(x)的极小值点,也是最小值点。文章来源地址https://www.toymoban.com/news/detail-421892.html
到了这里,关于最优化方法Python计算:一元函数导数计算的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!