算法刷刷刷|动态规划篇|509.斐波那契数| 70.爬楼梯| 746.使用最小花费爬楼梯| 62.不同路径| 63不同路径2| 343.正数拆分

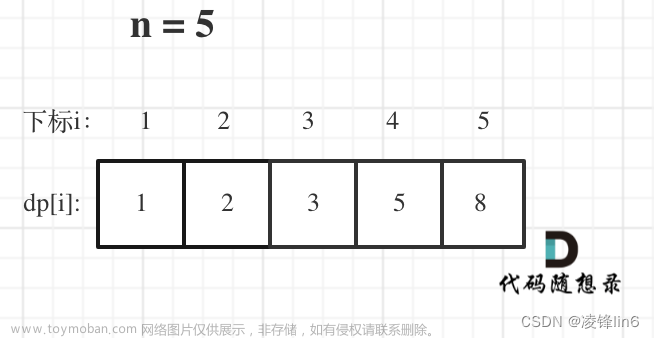
509. 斐波那契数

斐波那契数（通常用 F(n) 表示）形成的序列称为斐波那契数列。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：
F(0) = 0，F(1) = 1
F(n) = F(n - 1) + F(n - 2)，其中 n > 1
给定 n ，请计算 F(n) 。

public class Solution {

    public int fib(int n) {
        if (n <= 1) {
            return n;
        }
        int[] dp = new int[n + 1];
        dp[0] = 0;
        dp[1] = 1;
        for (int i = 2; i <= n; i++) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }
}

70.爬楼梯

class Solution {
    public int climbStairs(int n) {
        if (n <= 1) {
            return n;
        }
        int[] dp = new int[n + 1];
        dp[0] = 0;
        dp[1] = 1;
        dp[2] = 2;
        for (int i = 3; i <= n; i++) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }
}

746.使用最小花费爬楼梯

给你一个整数数组 cost ，其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用，即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
请你计算并返回达到楼梯顶部的最低花费。
示例 1：
输入：cost = [10,15,20]
输出：15
解释：你将从下标为 1 的台阶开始。

支付 15 ，向上爬两个台阶，到达楼梯顶部。
总花费为 15 。

class Solution {
    public int minCostClimbingStairs(int[] cost) {
        if (cost.length == 0) {
            return 0;
        }
        if (cost.length == 1) {
            return cost[0];
        }
        int[] dp = new int[cost.length + 1];
        dp[0] = 0;
        dp[1] = 0;
        for (int i = 2; i <= cost.length; i++) {
            dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
        }
        return dp[cost.length];
    }
}

62. 不同路径

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为 “Start” ）。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。
问总共有多少条不同的路径？

class Solution {
    public int uniquePaths(int m, int n) {
        int[][] dp = new int[m][n];
        for (int i = 0; i < m; i++) {
            dp[i][0] = 1;
        }
        for (int i = 0; i < n; i++) {
            dp[0][i] = 1;
        }
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
        return dp[m - 1][n - 1];
    }
}

63.不同路径II

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为 “Start” ）。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？
网格中的障碍物和空位置分别用 1 和 0 来表示。

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int m = obstacleGrid.length;
        int n = obstacleGrid[0].length;
        int[][] dp = new int[m][n];
        for (int i = 0; i < m && obstacleGrid[i][0] != 1; i++) {
            dp[i][0] = 1;
        }
        for (int i = 0; i < n && obstacleGrid[0][i] != 1; i++) {
            dp[0][i] = 1;
        }
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                if (obstacleGrid[i][j] != 1) {
                    dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
                } else {
                    dp[i][j] = 0;
                } 
            }
        }
        return dp[m - 1][n - 1];
    }
}

343.正数拆分

给定一个正整数 n ，将其拆分为 k 个正整数的和（ k >= 2 ），并使这些整数的乘积最大化。
返回你可以获得的最大乘积。文章来源地址https://www.toymoban.com/news/detail-422062.html

class Solution {
    public int integerBreak(int n) {
        if (n <= 2) {
            return 1;
        }
        int[] dp = new int[n + 1];
        dp[1] = 1;
        dp[2] = 1;
        for (int i = 3; i < n + 1; i++) {
            for (int j = 1; j <= i / 2; j++) {
                dp[i] = Math.max(dp[i], Math.max(j * (i - j), j * dp[i - j]));
            }
        }
        return dp[n];
    }
}

96.不同的二叉搜索树

class Solution {
    public int numTrees(int n) {
        if (n <= 2) {
            return n;
        }
        int[] dp = new int[n + 1];
        dp[0] = 1;
        dp[1] = 1;
        dp[2] = 2;
        for (int i = 3; i < n + 1; i++) {
            for (int j = 0; j < i; j++) {
                dp[i] += dp[j] * dp[i - j - 1];
            }
        }
        return dp[n];
    }
}