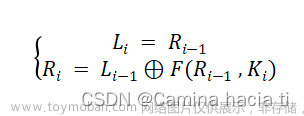参考blog:
密码学中的数学基础2
信道编码系列三
1. 域
域是一种定义了域中元素两种数学运算的代数系统,域由全体元素的加法集合以及非零元素的乘法集合构成。
性质:在加法和乘法上具有封闭性。
对域中元素进行加法或乘法运算后的结果仍然是域中元素。
PS: 域里面的乘法和加法可以是C语言中的与运算(module-2加法)和异或运算分别定义成加法和乘法。但习惯上,仍然使用符号+ 和 * 表示加法和乘法运算。
2. 域中单位元和逆元
加法和乘法运算都有对应的单位元(这两个单位元一般不同,但都用符号e表示):对于加法单位元,所有元素加上单位元e,等于其本身;对应乘法单位元,所有元素乘上单位e,等于其本身。
如果元素a在域中找不到另外一个元素b,使得a+b=e(a*b=e),那么a就没有加法(乘法)逆元。
PS: 0元素没有对应的乘法逆元
3. 有限域GF ( p ) (p) (p)
考虑这样一组整组构成的域 G = { 0 , 1 , 2 , 3 , … . . p − 1 } G = \{0, 1,2,3,….. p-1\} G={0,1,2,3,…..p−1}。其中p为素数,定义两种数学运算分别为 modulo-p加法和 module-p乘法。以p=7为例,加法和乘法分别为:
| 加 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 0 |
| 2 | 2 | 3 | 4 | 5 | 6 | 0 | 1 |
| 3 | 3 | 4 | 5 | 6 | 0 | 1 | 2 |
| 4 | 4 | 5 | 6 | 0 | 1 | 2 | 3 |
| 5 | 5 | 6 | 0 | 1 | 2 | 3 | 4 |
| 6 | 6 | 0 | 1 | 2 | 3 | 4 | 5 |
| 乘 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 |
| 2 | 2 | 4 | 6 | 1 | 3 | 5 |
| 3 | 3 | 6 | 2 | 5 | 1 | 4 |
| 4 | 4 | 1 | 5 | 2 | 6 | 3 |
| 5 | 5 | 3 | 1 | 6 | 4 | 2 |
| 6 | 6 | 5 | 4 | 3 | 2 | 1 |
为满足乘法的封闭性,显然p只能为素数。集合中元素个数为p。
性质(定理一): 如果 α \alpha α 是有限域GF ( p ) (p) (p) 中的非零元素,那么有 α p − 1 = 1 \alpha^{p-1}=1 αp−1=1
证明:设 b 1 , b 2 , … , b q − 1 b_{1}, b_{2}, \ldots, b_{q-1} b1,b2,…,bq−1为GF ( p ) (p) (p)中的p-1个非零元素,由于a也是非零元素,那么 a ⋅ b 1 , a ⋅ b 2 , … , a ⋅ b p − 1 a \cdot b_{1}, a \cdot b_{2}, \ldots, a \cdot b_{p-1} a⋅b1,a⋅b2,…,a⋅bp−1也是非零元素。
1)由p-1个元素的互异性得:
( a ⋅ b 1 ) ⋅ ( a ⋅ b 2 ) ⋯ ⋯ ( a ⋅ b q − 1 ) = b 1 ⋅ b 2 ⋯ ⋯ b q − 1 \left(a \cdot b_{1}\right) \cdot\left(a \cdot b_{2}\right) \cdots \cdots\left(a \cdot b_{q-1}\right)=b_{1} \cdot b_{2} \cdots \cdots b_{q-1} (a⋅b1)⋅(a⋅b2)⋯⋯(a⋅bq−1)=b1⋅b2⋯⋯bq−1
2)由乘法交换律得:
a q − 1 ( b 1 ⋅ b 2 ⋯ b q − 1 ) = b 1 ⋅ b 2 ⋯ ⋯ b q − 1 a^{q-1}\left(b_{1} \cdot b_{2} \cdots b_{q-1}\right)=b_{1} \cdot b_{2} \cdots \cdots b_{q-1} aq−1(b1⋅b2⋯bq−1)=b1⋅b2⋯⋯bq−1
4. 有限域GF ( 2 p ) (2^p) (2p)
将多项式的系数限定于有限域GF
(
p
)
(p)
(p)中的元素,并且基于有限域中的运算规则重新定义多项式的加减乘除操作,那么这样的多项式集合称为 基于有限域的多项式。
将GF
(
p
)
(p)
(p)扩展成GF
(
2
p
)
(2^p)
(2p),p不再仅限于素数,但仍然满足有限域的加法和乘法规则的思想:将有限域中的数值元素用多项式元素映射,即有限域GF
(
2
p
)
(2^p)
(2p)中的元素是包含0、1在内的
(
2
p
)
(2^p)
(2p)个多项式。
以GF ( 2 3 ) (2^3) (23)为例,指数小于 3 的多项式共 8 个: 0 , 1 , x , x + 1 , x 2 , x 2 + 1 , x 2 + x , x 2 + x + 1 0 , 1 , x , x+1 , x^2 , x^2+1 , x^2+x , x^2+x+1 0,1,x,x+1,x2,x2+1,x2+x,x2+x+1 。其系数刚好就是 000 , 001 , 010 , 011 , 100 , 101 , 110 , 111 000,001,010,011,100,101,110,111 000,001,010,011,100,101,110,111 ,是0 到7这8个数的二进制形式。多项式对应一个值,称这个值为多项式值。
4.1 有限域GF ( 2 p ) (2^p) (2p)的生成
生成元是域上的一类特殊元素,生成元的幂可以遍历域上的所有元素。假设g是域GF ( 2 p ) (2^p) (2p)上生成元,那么集合 { g 0 , g 1 , … … , g ( 2 p − 1 ) } \{g^0 ,g^1 , ……,g^{(2^p-1)} \} {g0,g1,……,g(2p−1)} 包含了域GF(2^p)上所有非零元素。
所以生成步骤为:
- 查表或手动计算得到p对应的本原多项式
- 本原多项式求幂得到 2 p − 2 2^p-2 2p−2个多项式
- 添加0、1形成域
4.2 GF ( 2 p ) (2^p) (2p)中的计算
加法和减法:
- 加法即异或运算
- 减法即加法
乘法和除法:
- 伽罗华域上的多项式乘法,其结果需要mod P(x)
实际实现中利用查表法解决,将二进制形式和多项式形式相互映射。每一个二进制数值对应的是本原多项式的多少次幂。
5.【GF域的具现化】
本原多项式
p
(
x
)
=
x
3
+
x
+
1
p(x)=x^{3}+x+1
p(x)=x3+x+1,
(1) 计算其本原根
α
\alpha
α 的复数值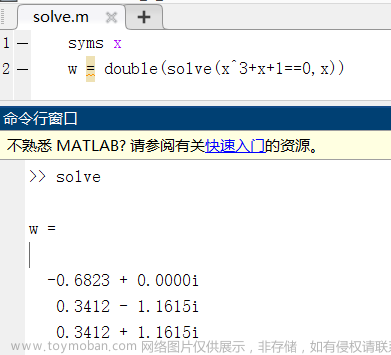
即本原多项式中
α
=
0.3412
+
1.1615
i
\alpha = 0.3412+1.1615i
α=0.3412+1.1615i
(2) 计算GF
(
2
3
)
\left(2^{3}\right)
(23) 内各个元素的复数值
GF ( 2 3 ) \left(2^{3}\right) (23)的多项式共 8 个: 0,1,x,x+1,x2,x2+1,x2+x,x2+x+10 , 1 , x , x+1 , x^2 , x^2+1 , x^2+x , x^2+x+1 。
其系数是 000,001,010,011,100,101,110,111000,001,010,011,100,101,110,111 ,是 0到 7的二进制形式。
下表给出了从本原根数值映射到多项式的过程
| 本原根 | 复数值 | 映射为多项式 | 多项式mod2 |
|---|---|---|---|
| 0 | 0 | ||
| α 0 α^0 α0 | 1 | α 0 α^0 α0 | α 0 α^0 α0 |
| α 1 α^1 α1 | α = 0.3412 + 1.1615 i \alpha = 0.3412+1.1615i α=0.3412+1.1615i | α 1 α^1 α1 | α 1 α^1 α1 |
| α 2 α^2 α2 | -1.2328 + 0.7926i | α 2 α^2 α2 | α 2 α^2 α2 |
| α 3 α^3 α3 | -1.3412 - 1.1615i | -α-1 | α+1 |
| α 4 α^4 α4 | 0.8916 - 1.9541i | − α 2 − α -α^2-α −α2−α | α 2 + α α^2+α α2+α |
| α 5 α^5 α5 | 2.5739 + 0.3690i | − α 2 − α + 1 -α^2-α+1 −α2−α+1 | α 2 + α + 1 α^2+α+1 α2+α+1 |
| α 6 α^6 α6 | 0.4495 + 3.1156i | α 2 + 2 ∗ α + 1 α^2+2*α+1 α2+2∗α+1 | α 2 + 1 α^2+1 α2+1 |
| α 7 α^7 α7 | -3.4656 + 1.5851i | 2 ∗ α 2 − 1 2*α^2-1 2∗α2−1 | 1 |
 文章来源:https://www.toymoban.com/news/detail-422194.html
文章来源:https://www.toymoban.com/news/detail-422194.html
(3) 验证域GF
(
2
3
)
\left(2^{3}\right)
(23)满足加法交换群和乘法交换群性质
参考1,c实现
参考2,python实现文章来源地址https://www.toymoban.com/news/detail-422194.html
到了这里,关于伽罗华域GF,GF(256)来源的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!