详解遗传算法与生产作业调度-Toy模板网

这篇具有很好参考价值的文章主要介绍了详解遗传算法与生产作业调度。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

🍎道阻且长，行则将至。🍓

一、遗传算法🌱

根据遗传学的理论，生物的进化发展来源于三大动力：自然选择、遗传和突变。自然选择就是自然环境对不同表现型生物有不同的影响，使用适应度来度量这种影响，适应度较好的生物个体对环境亲和力较高，有较大的几率可以存活下来，而适应度较差的容易被淘汰。遗传是指亲子之间或子代之间存在着相似的特点，由现代的遗传分子学说证明性状是由染色体上基因编码表达，适应度较高的个体基因编码可以更容易传递到下一代。变异则是染色体的基因编码发生异于父本的改变，导致性状发生改变，由于变异的不确定性，通常会带来不好的结果。遗传保证了生物的稳定性，变异促进了生物的多样性，在自然选择的作用下使生物能够不断进化发展。

而对于许多复杂的问题，例如函数优化和组合优化等，随着规模的扩大，约束的增加，问题变得更加复杂，以至于无法找到一种数值计算方法，那么如何在这样复杂的搜索空间寻求最优解。20世纪70年代美国密歇根大学John Holland等提出遗传算法，主要方法是模拟自然选择的演化过程构造人工系统模型，将问题的解作为一个个体进行合适的编码，将所有的编码抽象为一个种群，在种群内逐代进行选择、交叉、变异操作，以筛选出最优个体。

1.遗传算法简介

遗传算法就是对自然界生物演化的模拟，“物竞天择，适者生存…”我们都知道遗传学知识中有种群、个体、基因等，那么在遗传算法中同样也存在。
种群：自然界中生物一般以种群为单位生存，种群的大小表示问题解的规模。
个体：种群中单个生物由于基因的差别，表现出的性状也不一样，把个体作为算法中问题的解。
染色体、DNA、RNA：一种链状的有规则的编码结构。
基因：控制某种性状的编码片段。
遗传算法是模拟生物遗传过程，对待求问题进行分析，把所有解的集合视为一个种群，对问题的解进行适合的编码随机产生作为个体，设置一定的度量方式来评价每一个个体，自然选择则对应算法的选择操作，根据适应度函数，用一定的方法来选择个体，然后是繁殖后代，对应有算法的交叉和变异操作，随着时间的推进，种群逐渐具备更优良的品质，而达到一种稳定状态，种群中优良个体即为问题的较优解。

2.遗传操作

算法的三个核心计算：选择、交叉和变异0，每个操作也有不同的方案，对于不同的问题可以采取合适的方案来求解。

2.1 选择

通常我们是要挑选较优秀的个体出来，这个操作主要是通过选择概率进行的，而选择概率和适应度（根据函数计算的结果）有关，因此需要先计算每个个体的适应度。适应度计算之后挑选父代个体，主要方法有：

轮盘赌选择：模拟一种称为轮盘赌的游戏，选择概率与适应度有关：
将选择概率累加得到累积概率区间，然后随机产生一个概率值，包含在哪个区间范围则说明此次选中哪个个体。因此个体的适应度越高，即表示个体越优秀，选中该个体的概率也越大。
随机遍历抽样：和上一个方法轮盘赌类似，需要计算选择概率和累积概率区间，若种群的个体数目为m，先在0到1/m中随机产生一个数，此数值所在的区间代表的个体被选中，然后以1/m的距离在区间进行等距离抽样选择。
锦标赛选择：就是挑选一定数量个体参加比赛优者获胜，即随机参考一定数量个体，然后选择其中最好的。
局部选择：以种群中具有一定规则的部分个体为邻集，在这个邻集中选择父代个体。

2.2 交叉

交叉操作模拟生物的基因重组产生新个体，它的操作参数包括交叉的概率、位点和方式。根据编码类型的不同，包括实值交叉重组和二进制交叉重组，其中二进制交叉主要有以下几种方法：

单点交叉：若染色体编码长度为L，则在0~L随机取一个数k，以k为分界线进行交换。
多点交叉：在染色体长度内随机产生指定个数，作为本次交叉的交叉点，间隔进行交换。由于交叉的点较多，因此多点交叉的破坏性更强，可以在一定程度上增强算法搜索能力。
均匀交叉：对染色体编码每位以概率进行交换，这种方法类似于多点交叉。

而对于实数编码采用的是模拟二进制交叉方法。

2.3 变异

对个体的编码以较小的概率改变（遗传学中认为突变更可能带来不好的影响），属于局部随机搜索方法，根据编码方式的不同有实值变异和二进制变异。

3.遗传算法流程

步骤一：产生初始种群，使用合适的方式随机产生一定数目的编码；
步骤二：根据适应度函数计算适应度，判断是否符合结束要求，符合则结束并输出结果，否则继续计算；
步骤三：根据适应度按某种选择方法挑选父代个体；
步骤四：交叉，对父代进行交叉操作，生成下一代；
步骤五：变异，对个体的编码进行改变；
步骤六：产生新一代种群后返回步骤二。

详解遗传算法与生产作业调度

二、实现遗传算法🌴

遗传算法的主要流程就是编码、选择、交叉、变异，本节以遗传算法优化求解一个函数最大值为例进行实现和分析:

1.编码与初始化

编码是遗传算法的重要一步，编码有问题则后面的工作也无法继续，采取一个合适的编码方式可以有效提高遗传算法的运行效率。编码方式是一种解空间到搜索空间的映射，有浮点数和二进制数两种类型，浮点数编码在求解高精度问题上比较好，同时对复杂的约束条件处理也比较方便，二进制编码相比于浮点数编码具有操作简便的特点，但对于连续函数存在离散化的误差，使用较长的编码串可以提高精确度，可是会使得算法的搜索空间加大，降低遗传算法的性能。对于编码问题Goldberg提出编码评估规范：完备性、健全性和非冗余性。
在本节函数优化中，自变量的范围为[-1,2]，精确度为6位，解的空间大小为310⁶，由于2²¹< 310⁶ <2²², 进行二进制编码需要22位，通过下面的计算方法进行二进制编码：
详解遗传算法与生产作业调度
选择一个较好地种群规模可以提供遗传算法的运行效果，较小的种群规模可能降低算法的运行性能，而较大的规模可能会增加遗传算法的计算复杂度。初始化方法如下：

void  initpop(){
	int  j1 , k1 , m , end;
	unsigned  int g_mask  = 1;
	for (j1 = 0 ; j1 < popsize; j1++){  //popsize的种群
		for (k1 = 0; k1 < chrom_size; k1++){ 
			oldp[j1].chrom[k1] = 0;
			if (k1 == (chrom_size - 1))
				end = lchrom - (k1 * (8 * sizeof(unsigned int)));
			else
				end = 8 * sizeof(unsigned int);
			for (m = 1; m <= end;m++){
				oldp[j1].chrom[k1] = oldp[j1].chrom[k1] << 1;
				if (flip(0.5))
					oldp[j1].chrom[k1] = oldp[j1].chrom[k1] | g_mask;
			}
		}
		oldp[j1].parent[0] = 0; 
		oldp[j1].parent[1] = 0;
		oldp[j1].xsite = 0;
		fun_ob(&(oldp[j1])); 
	}
}

2.适应度计算和选择

根据目标函数计算值作为适应度，然后使用轮盘赌选择出子代。

void fun_ob(struct individual *p) {
	unsigned int g_mask = 1;
	unsigned int bit_p;
	unsigned int tp;
	double bit_po;
	int j, k, end;
	p->varible = 0.0;
	for (k = 0; k < chrom_size; k++){
		if (k == (chrom_size - 1))
			end = lchrom - (k*(8 * sizeof(unsigned int)));
		else
			end = 8 * sizeof(unsigned int);
		tp = p->chrom[k];
		for (j = 0; j < end; j++){
			bit_p = j + (8 * sizeof(unsigned int))*k;
			if ((tp&g_mask) == 1){
				bit_po = pow(2.0, (double)bit_p);
				p->varible = p->varible + bit_po;
			}
			tp = tp >> 1;
		}
	}
	p->varible = -1 + p->varible * 3 / (pow(2.0, (double)L_chrom) - 1);
	p->fitness = p->varible*sin(p->varible * 10 * atan(1.0) * 4) + 2.0;
}

3.交叉

交叉是对个体之间部分编码进行交换，是一种编码的处理方式。
单点交叉在染色体编码长度内随机选取一点作为交叉位点，对父代编码该点之前或之后的编码串进行交换。如对于以下两个父代编码：
父代1：1001 0101 1011
父代2：0111 0100 1100
若随机产生一个交叉位点为8，交叉后产生两个子代：
子代1：1001 0101 |1100
子代2：0111 0100 |1011

多点交叉就是在单点交叉的方法上产生多个交叉位点，多点交叉对模式的破坏性更强0，可以在一定程度上增强遗传算法的搜索能力，防止过早收敛，但是交叉概率不能设置太高，导致大量较高适应度的模式被破坏。如对于以下两个父代编码：
父代1：1001 0101 1011
父代2：0111 0100 1100
若随机产生的交叉位点为4、8、10，交叉后产生两个子代：
子代1：1001| 0100 |10|00
子代2：0111| 0101 |11|11

int g_cross (unsigned int *p1, unsigned int *p2, unsigned int *c1, unsigned int *c2) {
	int j, k, cross;
	unsigned int g_mask, tem;
	if (flip(pcross)){
		cross = rnd(1, (L_chrom - 1)); 
		ncross++;
		for (k = 1; k <= chrom_size; k++){
			if (cross >= (k*(8 * sizeof(unsigned int)))){
				c1[k - 1] = p1[k - 1];
				c2[k - 1] = p2[k - 1];
			}
			else if((cross<(k*(8 * sizeof(unsigned int)))) && (cross >((k - 1)*(8 *sizeof(unsigned int))))){
				g_mask = 1;
				for (j = 1; j <= (cross - 1 - ((k - 1)*(8 * sizeof(unsigned int)))); j++){
					tem = 1;
					g_mask = g_mask << 1;
					g_mask = g_mask | tem;
				}
				c1[k - 1] = (p1[k - 1] & g_mask) | (p2[k - 1] & (~g_mask));
				c2[k - 1] = (p1[k - 1] & (~g_mask)) | (p2[k - 1] & g_mask);
			}
			else{
				c1[k - 1] = p2[k - 1];
				c2[k - 1] = p1[k - 1];
			}
		}
	}
	else{
		for (k = 0; k < chrom_size; k++){
			c1[k] = p1[k];
			c2[k] = p2[k];
		}
		cross_p = 0;
	}
	return(cross_p);
}

3.突变

子代个体编码以小概率或步长进行改变。对于二进制的编码方式，变异就是以概率将染色体编码某一位取反。

void mutation(unsigned int *p) {  
	int j, k, end;
	unsigned int g_mask, tem = 1;
	for (k = 0; k < chrom_size; k++){
		g_mask = 0;
		if (k == (chrom_size - 1))
			end = L_chrom - (k*(8 * sizeof(unsigned int)));
		else
			end = 8 * sizeof(unsigned int);
		for (j = 0; j < end; j++){
			if (flip(p_mutation))	{
				g_mask = g_mask | (tem << j);
				n_mutation++;	}
		}
		p[k] = p[k] ^ g_mask;
	}
}

进化过程

模拟种群世代的进化过程，先预先设定种群的参数，包括种群大小、染色体编码长度、遗传操作的概率和计算的代数，然后根据参数对种群初始化，每一代调用generation函数进行计算，然后将新一代个体作为父代再进行下一轮计算，这样循环到指定代数结束。

for (gen = 0; gen < m_gen; gen++){
generation();
bestm = statistics(newp);
newp[bestm].keep = 1;
tem = oldp;
oldp = newp;
newp = tem;
}

void generation(){
	int parte1, parte2, cross_p, j = 0, k = 0;
	preselect();
	int prot = popsize*0.05;
	if (prot % 2 == 1)
		prot++; 
	j = prot;
	protect_mate(prot);
	do{
		parte1 = select();
		parte2 = select();
		cross_p = g_cross_p(oldp[parte1].chrom, oldp[parte2].chrom, newp[j].chrom, newp[j + 1].chrom);
		mutation(newp[j].chrom);
		mutation(newp[j + 1].chrom);
		fun_ob(&(newp[j]));
		newp[j].parent[0] = parte1 + 1;
		newp[j].xsite = cross_p;
		newp[j].parent[1] = parte2 + 1;
		fun_ob(&(newp[j + 1]));
		newp[j + 1].parent[0] = parte1 + 1;
		newp[j + 1].xsite = cross_p;
		newp[j + 1].parent[1] = parte2 + 1;
		j = j + 2;
	} while (j < (popsize - 1));
}

调用EasyX库进行绘图

同时实现了使用文件存储每一代个体情况。源代码下载👉看这里
详解遗传算法与生产作业调度

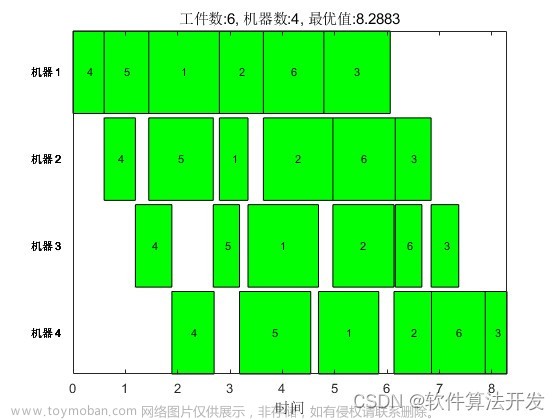
三、作业调度🌴

作业调度问题就是对资源进行合理分配使产生最大的效益，对于车间生产的问题考虑的主要是设备资源如何规划，让车间生产工作有条不紊的进行同时做到高效。基于前面遗传算法的基础，这一节我们采用遗传算法进行车间作业调度优化。

1.调度模型

工厂车间调度实际要考虑的问题比计算的更复杂，在实验中对问题进行简化讨论，假设某机器用于工业生产，可以生产多种组件，每个组件在进行生产前需要使用夹具来固定，每个夹具可以固定不同数目的组件，一天可以使用的夹具数目有限，不同的组件有不同的完工时间要求，对于一个组件有多项生产要求，包括交工时间、需要完成的数量、当天可以使用的夹具数量，要求制定一个较好地加工计划完成生产任务。对于这里的调度问题，有以下约束条件：每日的总工作时间，考虑到机器和生产能力，每天的累积工作时长不超过11天；加工机器每天可用的工具总个数不超过100个；总生产任务在交工期限之前完成；夹具数量约束。
以最小交工时间为目标进行调度规划，使用数学符号建立相应的数学模型。

符号	说明	符号	说明
i	组件编号	j	加工的天数
t_ij	组件i第j天的加工时间	b_ij	组件i第j天使用的夹具数
c_ij	组件i第j天使用的工具数	a_ti	组件i的总加工时间
^b_i	组件i可使用的夹具数	f_i	组件i的交工时间
N_i	组件i加工日期的集合

可以建立对应目标函数为：
约束条件：

2.遗传算法应用

使用遗传算法完成作业调度最优计算，首先对结果选取合适的编码方式，一个调度方案作为个体，这个方案的元素包括不同组件、对应组件的加工时间安排，因此使用一个数组保存比较方便，由于不同组件的加工时间不同，随机生成的一个时间可能不能完整加工一个组件，因此需要对此时间进行修正，考虑到这样的修正处理可能比较多，使得运算效率下降，这里采用夹具数来代替，同时考虑夹具数的约束。
选取好合适的编码表示方法后随机生成初始种群，先将矩阵置0，组件在矩阵的列方向排列，依次处理每列，先处理第一个组件，对所在的行任意元素选取一个可选加工日，添加可选的夹具数目，直到达到该组件的总夹具数，接下来继续同样的方法处理后面的组件，当所有组件处理完成后检查是否符合约束条件，符合则计算出目标函数值，否则继续。
选择操作基于排序选择，按目标值排序，使用预定的淘汰比例去掉一部分目标函数值高的个体，对剩下的进行选择。之后进行交叉操作，也是随机产生一个交叉位点，对选取的两父本部分进行交换，由于约束条件的存在，需要在交叉之后对个体进行修正，主要就是考虑哪个组件使用的夹具数过多，哪个组件使用的夹具数不够，对于过多的则随机选取一天慢慢减少夹具数直到满足要求，过少的组件就要在约束的天数内，同时要考虑列的夹具要求，随机选取选取合适的一天慢慢增加夹具数，如果存在某个无论怎么修正都不符合的，就认为这个个体交叉致死，进行淘汰处理。
之后就对个体进行变异操作，在交工时间数内随机产生两个数作为两列标号，交换这两列，这样的操作有可能会产生不满足交工时间的约束，而其他的约束都是符合的，所以出现这种情况就对个体进行重新突变，使得满足交工时间的约束。

3.实现

详解遗传算法与生产作业调度

源代码接测试文件下载👉
主要代码如下：

%% load数据
load test2 Jm T JmNumber
%工序 时间

%% 基本参数
NIND=200;        %个体数目
MAXGEN=1000;      %最大遗传代数
GGAP=0.6;       %代沟
XOVR=0.9;       %交叉率
MUTR=0.05;       %变异率
gen=0;          %代计数器
%PNumber 工件个数 MNumber  工序个数
[PNumber ,MNumber]=size(Jm);
trace=zeros(2, MAXGEN);      %寻优结果的初始值
WNumber=PNumber*MNumber;     %工序总个数

%% 初始化
Number=zeros(1,PNumber);     % PNumber 工件个数
for i=1:PNumber
    Number(i)=MNumber;         %MNumber工序个数
end

% 代码2层，第一层工序，第二层机器
Chrom=zeros(NIND,2*WNumber);        %0矩阵
for j=1:NIND
    WPNumberTemp=Number;
    for i=1:WNumber
        
        %随机产成工序
        val=unidrnd(PNumber);       %1到P的随机数
        while WPNumberTemp(val)==0
            val=unidrnd(PNumber);
        end
        
        %第一层代码表示工序
        Chrom(j,i)= val;
        WPNumberTemp(val)=WPNumberTemp(val)-1;
        
        %第2层代码表示机器
        Temp=Jm{val,MNumber-WPNumberTemp(val)};
        SizeTemp=length(Temp);
        %随机产成工序机器
        Chrom(j,i+WNumber)= unidrnd(SizeTemp);
        
    end
end

%计算目标函数值
[PVal, ObjV ,P, S]=cal(Chrom,JmNumber,T,Jm);

while gen<MAXGEN
    
    %分配适应度值
    FitnV=ranking(ObjV);
    %选择操作
    SelCh=select('rws', Chrom, FitnV, GGAP);
    %交叉操作
    SelCh=across(SelCh,XOVR,Jm,T);
    %变异操作
    SelCh=aberranceJm(SelCh,MUTR,Jm,T);
    
    %计算目标适应度值
    [PVal, ObjVSel ,P ,S]=cal(SelCh,JmNumber,T,Jm);
    %重新插入新种群
    [Chrom, ObjV] =reins(Chrom, SelCh,1, 1, ObjV, ObjVSel);
    %代计数器增加
    gen=gen+1;
    
    %保存最优值
    trace(1, gen)=min(ObjV);
    trace(2, gen)=mean(ObjV);
    
    % 记录最佳值
    if gen==1
        Val1=PVal;
        Val2=P;
        MinVal=min(ObjV);%最小时间
        STemp=S;
    end
    %记录 最小的工序
    if MinVal>trace(1,gen)
        Val1=PVal;
        Val2=P;
        MinVal=trace(1,gen);
        STemp=S;
    end    
end

% 当前最佳值
PVal=Val1; %工序时间
P=Val2;  %工序
S=STemp; %调度基因含机器基因

四、遗传算法的数学分析🌲

1.模式定理

遗传算法是逐代从种群中搜索最优个体，每个个体对应一个编码，不同的个体之间由于编码的规则存在一些相似的编码结构，因此搜索最优个体的过程就是对编码结构的处理过程。
模式指的是种群中个体编码串的相似结构模板，也就是相似的构型，代表一类具有某种共同特点个体的集合。在二进制编码串中，模式由1、0、*这三个字符表示。由于不确定字符的存在使得模式之间具有不同的特性，有些表示的编码更加确定:
模式H1(1*** ***0)与模式H2(101**110)相比，H2表示的确定位更多，模式内编码的差异性越小，表示的个体越确定；有些模式比其他模式表示的确定位更密集;
比如模式H3(1*** ***0)与模式H4(1**1* ****)相比，H4表示的确定位更集中，这样的模式在遗传操作过程中更稳定。

下面给出模式阶和定义距的概念来表达这种关系：

模式阶：模式的确定位的个数，记为O(H)，例如O(100* **10)=4。
定义距：模式中第一个确定位到最后一个确定位的距离，记为σ(H)，如σ(10** 1*1*)=6。

在大小为n的种群S第t代S(t)中，设模式H有k个代表串，记为k(H,t)，在生成下一代时每个编码串以适应度为标准进行复制，可用公式表示：
详解遗传算法与生产作业调度

其中f(H)是模式H的平均适应度，若用表示种群的平均适应度，则又可以表示为:
详解遗传算法与生产作业调度

表明模式H的代表串个数在代际间呈线性变化。若模式的平均适应度f(H)=cU,c为常数，则模式H的变化方程可以表示为：
详解遗传算法与生产作业调度
交叉和变异对模式的影响:

假设一个串c的编码为1001 0011，可以同时包含在模式H1：1*0* **1*和模式H2：*0** 0***，交叉位置随机在1~7，若交叉点为1、5、6，则模式H1被破坏，模式H2保留到下一代，可以看出模式H2更稳定。一般情况下长度为j的模式被破坏的概率为σ(H)/(j-1)。对于变异操作，若以概率p随机改变一位编码，如果模式串H有一个确定位在计算过程中被改变了，说明这个模式没有被保留下来，则H1保留下来的概率为(1-p)³ ，H2保留下来的概率为(1-p)²。一般情况下模式H保留下来的概率为(1-p)^O(H)。

模式定理：具有低阶、短定义距和平均适应度高于种群的模式以指数增长。说明了较优模式在计算过程中以较快的速度增长，获得更多较好的解。

2.积木块假设

积木块假设是将每个模式作为一个积木模型的潜在组件，只有选择出合适的组件来拼接组合才可以构造出最后的目标物。积木块就是这样合适的组件：具有低阶、短定义距和平均适应度高于种群的模式。积木块在遗传操作过程中的拼接结合，出现更优秀的个体，最后产生全局最优解。
模式定理使得较优模式在子代可以快速增长，满足遗传算法求最优解的条件，而积木块假设表明遗传算法具有求最优解的能力。

3.收敛性分析

交叉概率和变异概率的选择对计算影响较大，选择的概率过大或者过小也会影响收敛速度，最优个体保护机制让每一代的最优个体总可以保留到下一代，最后计算最优个体达到一个较大值后不在增长，即开始收敛。模式定理虽然给出了模式H随代数的变化关系，但是我们仍然无法由此得出算法的收敛性。在最优解和积木块有冲突的情况下，就可能收敛到一个非最优的解，这通常和编码方式、适应度函数的设置有关。
若某个种群中，用4位二进制对个体编码，使用的适应度函数为g(x)，其中个体m1(1000)为最优，并且g(0***)=82,g(1***)=36，模式H1（0***）>H2(1***)，就可能会妨碍模式H2的生成，出现更多模式H1的个体，对这样的情况一般采取对适应度函数进行调整。

参考文献：
[1]Mirjalili S, Mirjalili S. Genetic algorithm[J]. Evolutionary Algorithms and Neural Networks: Theory and Applications, 2019: 43-55.
[2]王小平, 曹立明. 遗传算法: 理论, 应用及软件实现[M]. 西安交通大学出版社, 2002.
[3]Forrest S. Genetic algorithms[J]. ACM computing surveys (CSUR), 1996, 28(1): 77-80.
[4]Holland J H. Genetic algorithms[J]. Scientific american, 1992, 267(1): 66-73.