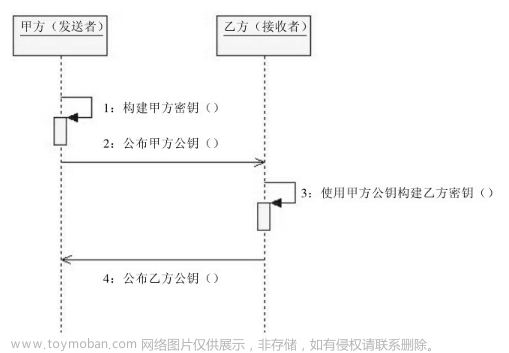
不同于传统的对称加密算法体系,非对称公私钥密码系统中的加密密钥和解密密钥是相互分开的,加密密钥用于公开给别人加密,而只有持有解密密钥的人才能对信息进行解密。1976年诞生过不少非对称密码算法,但是RSA是其中最容易让人理解的。下文将尝试对RSA实现的具体流程进行解析。
寻找合适的加密、解密函数
我并不知道RSA最初的诞生经过了怎样的启发与灵光一闪,但仍有办法切入RSA的设计思路,现在,我们从它的实际效果:公钥加密,私钥解密来入手,尝试一步步分析它,了解它。
我们首先面临的问题是,如果想要达到加解密的钥匙分开的效果,应当怎么做呢?
先尝试使用数学语言抽象化描述一下这个问题:
设加密函数为 f 1 ( m , e ) f_1(m,e) f1(m,e),m为明文,e为加密密钥,解密函数为 f 2 ( x , d ) f_2(x,d) f2(x,d),x为密文,d为解密密钥,那么,我们需要寻找函数 f 1 f_1 f1和 f 2 f_2 f2,使得: m = f 2 ( f 1 ( m , e ) , d ) m=f_2(f_1(m, e),d) m=f2(f1(m,e),d)成立,经过函数 f 1 f_1 f1和 f 2 f_2 f2两次变换之后,我们需要能够把明文给还原回来。
为了解决上面的问题,我们需要对两个数学知识有一定的了解,第一个是欧拉定理,第二个则是模算术。
欧拉定理
若 a , m 均为正整数 , 且 g c d ( a , m ) = 1 , 则 a φ ( m ) ≡ 1 ( m o d m ) 若a,m均为正整数,且gcd(a,m)=1,则a^{\varphi(m)}\equiv 1 (\mod m) 若a,m均为正整数,且gcd(a,m)=1,则aφ(m)≡1(modm)
g c d ( a , m ) gcd(a,m) gcd(a,m)表示求数a和m的最大公因数,如果最大公因数为1,这两个数互质。
其中 φ ( m ) \varphi(m) φ(m)是一个重要的数论函数:欧拉函数。 φ ( m ) \varphi(m) φ(m)表示小于等于m的正整数中与m互质的数的数目。显然,若m为素数,则 φ ( m ) = m − 1 \varphi(m)=m-1 φ(m)=m−1。
基本的模算术
如果A和B满足 A m o d n = B m o d n A \mod n=B\mod n Amodn=Bmodn,我们称之为A与B有同余关系,同余关系常常又表示成: A ≡ B ( m o d n ) A\equiv B (\mod n) A≡B(modn)。同余关系是一种等价关系。
模的含义可以换算为普通乘式:
A
m
o
d
B
=
C
→
A
=
k
B
+
C
A\mod B=C \rightarrow A=kB+C
AmodB=C→A=kB+C
基本的模加法和模乘法、模幂运算规则如下:
(
A
+
B
)
m
o
d
C
=
(
A
m
o
d
C
+
B
m
o
d
C
)
m
o
d
C
(
A
∗
B
)
m
o
d
C
=
(
(
A
m
o
d
C
)
∗
(
B
m
o
d
C
)
)
m
o
d
C
(
A
B
)
m
o
d
C
=
(
A
m
o
d
C
)
B
m
o
d
C
(A + B) \mod C = (A \mod C + B \mod C) \mod C \\ (A * B) \mod C = ((A \mod C) * (B \mod C)) \mod C \\ (A^B)\mod C = (A\mod C)^B \mod C \\
(A+B)modC=(AmodC+BmodC)modC(A∗B)modC=((AmodC)∗(BmodC))modC(AB)modC=(AmodC)BmodC
了解了模幂的规则,其实我们很快就能发现函数 f ( a , x ) = a x m o d m f(a,x)=a^x\mod m f(a,x)=axmodm很有趣,因为存在 f ( f ( a , e ) , d ) = f ( a , e d ) f(f(a,e),d)=f(a,ed) f(f(a,e),d)=f(a,ed),即 ( a e m o d m ) d m o d m = a e d m o d m (a^e \mod m)^d \mod m = a^{ed} \mod m (aemodm)dmodm=aedmodm成立,而 a e d m o d m a^{ed} \mod m aedmodm与 a φ ( m ) ≡ 1 ( m o d m ) a^{\varphi(m)}\equiv 1 (\mod m) aφ(m)≡1(modm)之间的相似度又不禁令我们遐想联翩。实际上,欧拉定理再变通一下,我们就能得
到 a φ ( m ) + 1 m o d m = a a^{\varphi(m)+1}\mod m=a aφ(m)+1modm=a,**其中 a < m a<m a<m。**那么,要是 e d = φ ( m ) + 1 ed=\varphi(m)+1 ed=φ(m)+1的话,不就有 a e d m o d m = a φ ( m ) + 1 m o d m = a a^{ed} \mod m=a^{\varphi(m)+1}\mod m=a aedmodm=aφ(m)+1modm=a了吗?!那么,我们现在这样来描述我们的加解密函数 f 1 f_1 f1和 f 2 f_2 f2,令 f 1 = f 2 = a x m o d m f_1=f_2=a^x\mod m f1=f2=axmodm,其中a为明文,选择一个 m m m,计算 φ ( m ) \varphi(m) φ(m),公钥和私钥的策略是,然后选择一个 e e e并根据 e d = φ ( m ) + 1 ed=\varphi(m)+1 ed=φ(m)+1计算 d d d。
经过上面的简单思考,我们来解决一些随之而来的问题。
首先,我们为了得到 a φ ( m ) + 1 m o d m = a a^{\varphi(m)+1}\mod m=a aφ(m)+1modm=a,实际上弱化了欧拉定理,要求底数 a < m a<m a<m。不过这并不是什么大问题,底数a代表的明文如果实在太长,我们把它分割一下,让它小于m就行了。
其次,欧拉定理还要求底数a和模m互质( g c d ( a , m ) = 1 gcd(a,m)=1 gcd(a,m)=1),这是一个比较严苛的要求。幸运的是,即使明文a与m不互质,我们也可以证明我们的加密、解密函数仍然有效,稍后将给出证明。
另外,在实现上仍有诸多疑问:一个数的幂的结果增长得特别快,计算 a e d a^{ed} aed是否很容易超出编程语言中整型变量的范围呢?如何根据 n n n确定 φ ( n ) \varphi(n) φ(n)?
快速模幂
我们先来解决计算 a e d m o d n a^{ed}\mod n aedmodn的问题。
例如,要求计算
2
256
m
o
d
7
2^{256}\mod 7
2256mod7。显然,先计算出
2
256
2^{256}
2256不是什么明智的选择。根据模算术的基本规则,我们可以得到:
2
256
m
o
d
7
=
(
2
128
m
o
d
7
∗
2
128
m
o
d
7
)
m
o
d
7
2^{256}\mod 7=(2^{128}\mod 7*2^{128}\mod7)\mod7
2256mod7=(2128mod7∗2128mod7)mod7
如何求
2
128
m
o
d
7
2^{128}\mod 7
2128mod7呢?答案是去求解
2
64
m
o
d
7
2^{64}\mod 7
264mod7,这样循环递归下去,我们可以凭借
2
m
o
d
7
2\mod 7
2mod7的结果计算
2
256
m
o
d
7
2^{256}\mod 7
2256mod7!这是基于分治思想得出的算法。
不过,如果幂不能被2整除呢?例如求 3 117 m o d 7 3^{117}\mod 7 3117mod7。这时,关键在于如何对整数117按照2的若干次幂进行划分,其实117的二进制表示本身就是一种天然划分。把117表示成二进制: 117 = ( 1110101 ) 2 117=(1110101)_2 117=(1110101)2, 3 117 = 3 2 0 + 2 2 + 2 4 + 2 5 + 2 6 = 3 1 ∗ 3 4 ∗ 3 16 ∗ 3 32 ∗ 3 64 3^{117}=3^{2^0+2^{2}+2^{4}+2^{5}+2^{6}}=3^1*3^4*3^{16}*3^{32}*3^{64} 3117=320+22+24+25+26=31∗34∗316∗332∗364
我们可以使用动态规划的思想,自底向上进行迭代来求解这个问题。
分析递推式,有 2 k m o d n = ( 2 k − 1 m o d n ) 2 m o d n 2^k\mod n=(2^{k-1}\mod n)^2\mod n 2kmodn=(2k−1modn)2modn,事实上动态规划表内第k项只和第k-1项有关,我们可以省略一个完整的动态规划表,只保留k-1项。
public static int fastModularExponentiation(int base, int power, int p) {
// 缓存k-1项
int i = base % p;
int result = 1;
while (power > 0) {
if ((power & 1) == 1) {
result = (result * i) % p;
}
i = (i * i) % p;
power = power >> 1;
}
return result;
}
如何产生n与如何计算 φ ( n ) \varphi(n) φ(n)
因为我们选定了 f ( m , e ) = m e m o d n f(m,e)=m^e\mod n f(m,e)=memodn来进行加密运算,那么公钥e和模n都需要公开,其他人才可以进行加密。 n n n被公开则触及一个核心的问题:既然 n n n被公开, φ ( n ) \varphi(n) φ(n)不是很容易被计算出来吗?又有 e d = φ ( n ) + 1 ed=\varphi(n)+1 ed=φ(n)+1,那么密钥 d d d不是很容易确定吗?这样还存在保密性吗?
首先,对于一个合数而言,欧拉函数 φ ( n ) \varphi(n) φ(n)的值其实不那么容易被计算出来,因为没有有效的算法来计算甚至估算这个函数的值,我们只能暴力地从1到 n − 1 n-1 n−1,一个个去尝试它是否与n互质。问题随之而来,如果公开的模n复杂到别人无法暴力破解 φ ( n ) \varphi(n) φ(n),那么我们又凭什么能够快速算出 φ ( n ) \varphi(n) φ(n)呢?算法又需要这个值来生成公钥和私钥。
下面的这个定理完美解决了上述问题
若
p
和
q
都是素数,
n
=
p
q
,那么
φ
(
n
)
=
φ
(
p
)
φ
(
q
)
若p和q都是素数,n=pq,那么\varphi(n)=\varphi(p)\varphi(q)
若p和q都是素数,n=pq,那么φ(n)=φ(p)φ(q)
以上定理不作证明,我们使用这个定理,轻易就能得出
φ
(
n
)
=
(
p
−
1
)
(
q
−
1
)
\varphi(n)=(p-1)(q-1)
φ(n)=(p−1)(q−1),也就是说,只要找到n的两个素数因子,我们就能确定
φ
(
n
)
\varphi(n)
φ(n),以这种思路来计算
φ
(
n
)
\varphi(n)
φ(n)的可行性基本上是……0。是的,当n相当大的时候,找出两个素数因子简直难如登天。我们不是采用这种方法来计算
φ
(
n
)
\varphi(n)
φ(n),而是以这种思路来生成
n
n
n,从而不费吹灰之力得到
φ
(
n
)
\varphi(n)
φ(n):先选择两个大素数p和q,然后计算n=pq,
φ
(
n
)
\varphi(n)
φ(n)自然等于
(
p
−
1
)
(
q
−
1
)
(p-1)(q-1)
(p−1)(q−1),而公开的公钥对{e,n}中,别人只拿到了n,想计算出
φ
(
n
)
、
p
、
q
\varphi(n)、p、q
φ(n)、p、q反而相当困难。
公钥e和私钥d的生成
既然我们已经调整了n的生成过程,其实公钥e和私钥d的生成过程我们也需要调整了。因为要求 e d = φ ( n ) + 1 ed=\varphi(n)+1 ed=φ(n)+1不一定能得到满足,我们不能保证 φ ( n ) + 1 \varphi(n)+1 φ(n)+1一定是一个合数,为此不停生成n显得有点本末倒置,我们希望能够得到一个更简洁的公钥私钥生成过程。
e d = φ ( n ) + 1 ed=\varphi(n)+1 ed=φ(n)+1不一定成立?没关系,我们可以加入一个系数k,构造 e d = k ∗ φ ( n ) + 1 ed=k*\varphi(n)+1 ed=k∗φ(n)+1,k为整数,当k=1时不成立也不要紧,只要有一个k能使得上述式子成立就行了。加上k之后, e d ed ed的含义并没有改变,因为 a φ ( n ) ≡ 1 ( m o d n ) a^{\varphi(n)}\equiv 1 (\mod n) aφ(n)≡1(modn)成立意味着 a k φ ( n ) + 1 ≡ a ( m o d n ) a^{k\varphi(n)+1}\equiv a (\mod n) akφ(n)+1≡a(modn)也成立。
先不讨论是否真的存在一个这样的k,我们先来化简一下这个式子。还记得模与普通算式的转换吗?
e
d
=
k
∗
φ
(
n
)
+
1
→
e
d
≡
1
(
m
o
d
φ
(
n
)
)
ed=k*\varphi(n)+1\rightarrow ed\equiv 1(\mod \varphi(n))
ed=k∗φ(n)+1→ed≡1(modφ(n))
然后,上述式子还可以写为
d
=
e
−
1
m
o
d
φ
(
n
)
d= e^{-1}\mod \varphi(n)
d=e−1modφ(n)
d称之为e的模逆元,不过e的模逆元的意思可不是e的倒数求模,而是求一个数d能使得e与d的乘积与1同余。
经过修改,我们暂时把公钥e和私钥d的生成过程描述如下:
选择一个公钥
e
,计算私钥
d
=
e
−
1
m
o
d
φ
(
n
)
。
选择一个公钥e,计算私钥d= e^{-1}\mod \varphi(n)。
选择一个公钥e,计算私钥d=e−1modφ(n)。
现在我们再来思考这个问题:是否存在一个整数k,使得
e
d
=
k
∗
φ
(
n
)
+
1
ed=k*\varphi(n)+1
ed=k∗φ(n)+1成立呢?如果不成立,私钥d就不存在了。需要什么前提条件使得k存在吗?
解决这个问题需要引入线性同余方程的概念。
在数论中,形如
a
x
≡
b
(
m
o
d
n
)
的形式的方程称之为线性同余方程
在数论中,形如ax\equiv b(\mod n)的形式的方程称之为线性同余方程
在数论中,形如ax≡b(modn)的形式的方程称之为线性同余方程
此方程有解当且仅当
b
b
b能够被
a
a
a与
n
n
n的最大公因数整除。该性质的详细证明忽略。由该性质得到下面的引理:
设
a
和
b
不全为
0
,则存在整数
x
,
y
,使得
g
c
d
(
a
,
b
)
=
a
x
+
b
y
设a和b不全为0,则存在整数x,y,使得gcd (a,b)=ax+by
设a和b不全为0,则存在整数x,y,使得gcd(a,b)=ax+by
我们拿出方程式
e
d
≡
1
(
m
o
d
φ
(
n
)
)
ed\equiv 1(\mod \varphi(n))
ed≡1(modφ(n))对比上面的同余方程一般式,就能发现,只要e和
φ
(
n
)
\varphi(n)
φ(n)的最大公因数为1(它们互质),那么方程的解就存在,也就是私钥d存在。
既然证明了私钥d是存在的,剩下的问题则是如何计算它。计算私钥d的核心思想是扩展欧几里得算法。
提到欧几里得算法(GCD),相比各位不会陌生,这是一个求数A和B的最大公因数的高效算法,我们有
g
c
d
(
a
,
b
)
=
g
c
d
(
b
,
a
m
o
d
b
)
gcd(a,b)=gcd(b, a\mod b)
gcd(a,b)=gcd(b,amodb)
该算法正确性的证明不作讨论,我们仅关注怎么使用它来解决同余方程,计算出我们想要的私钥d。
下面是扩展欧几里得算法的思路:
g
c
d
(
a
,
n
)
=
a
x
1
+
n
y
1
g
c
d
(
n
,
a
%
n
)
=
n
x
2
+
(
a
%
n
)
y
2
=
n
x
2
+
(
a
−
a
/
n
∗
n
)
∗
y
2
=
n
x
2
+
a
y
2
−
a
/
n
∗
n
∗
y
2
=
a
y
2
+
n
(
x
2
−
a
/
n
∗
y
2
)
gcd(a,n)=ax_1+ny_1 \\ gcd(n, a \% n) = nx_2+(a\% n)y_2\\ =nx_2+(a-a/n*n)*y_2 \\ = nx_2+ay_2-a/n*n*y_2 \\ =ay_2+n(x_2-a/n*y_2) \\
gcd(a,n)=ax1+ny1gcd(n,a%n)=nx2+(a%n)y2=nx2+(a−a/n∗n)∗y2=nx2+ay2−a/n∗n∗y2=ay2+n(x2−a/n∗y2)
因为
g
c
d
(
a
,
n
)
=
g
c
d
(
n
,
a
%
n
)
gcd(a,n)=gcd(n, a \% n)
gcd(a,n)=gcd(n,a%n),所以
x
1
=
y
2
,
y
1
=
x
2
−
a
/
n
∗
y
2
x_1=y_2,y_1=x_2-a/n*y_2
x1=y2,y1=x2−a/n∗y2,我们得到了计算a与n的最大公因数的过程中x和y的递推公式,据此可以写出算法的简单实现代码。
public static int x = 0;
public static int y = 0;
/**
* 计算ax+ny=1的特解
*/
public static int gcd(int a, int n) {
if (n == 0) {
x = 1;
y = 0;
return a;
} else if (a == 0) {
x = 0;
y = 1;
return n;
} else {
int c = gcd(n, a % n);
int tmp = x;
x = y;
y = tmp - a / n * y;
return c;
}
}
上面的静态变量x就是我们想要的私钥d。现在,生成私钥d已经不是难题了。
RSA算法全过程
我们已经差不多把RSA算法的全过程都解释了一遍,现在来浏览一下真正的RSA算法全过程吧。
密钥生成
- 选择大素数p与q,计算 n = p q n=pq n=pq, φ ( n ) = ( p − 1 ) ( q − 1 ) \varphi(n)=(p-1)(q-1) φ(n)=(p−1)(q−1),然后丢弃p和q,不保留。
- 在 1 < e < φ ( n ) 1<e<\varphi(n) 1<e<φ(n)的范围内选择整数公钥e,使得 g c d ( e , φ ( n ) ) = 1 gcd(e,\varphi(n))=1 gcd(e,φ(n))=1(若 e e e和 φ ( n ) \varphi(n) φ(n)不互质,则不存在私钥 d d d,这点上面已经证明过了)。
- 计算私钥d, d = e − 1 m o d φ ( n ) d=e^{-1}\mod \varphi(n) d=e−1modφ(n)。
加密过程
- 发送方获得公钥对{e,n}
- 把明文 m m m分解为小于n的若干块
- 计算密文 C = m e m o d n C=m^e\mod n C=memodn
解密过程
- 接收方提前内置密钥对{d,n}
- 对密文解密 m = C d m o d n m=C^d\mod n m=Cdmodn
尾声:RSA算法正确性证明
回到我们最开始先忽略的那一个问题,既然欧拉定理要求底数a与模n互质,当明文a与模n不互质的时候,还能够完成加密并解密的任务吗?先给出结论,结论是只要a不是模n的倍数,RSA算法就是正确的。既然我们要求了 a < n a<n a<n,那么a是n的倍数的可能性不复存在。
以下是证明:
设
n
=
p
q
,
a
是某一个整数、
g
c
d
(
a
,
n
)
≠
1
且
a
不能被
n
整除,试证明
a
≡
a
k
φ
(
n
)
+
1
(
m
o
d
n
)
设n=pq,a是某一个整数、gcd(a,n)\neq 1 且a不能被n整除,试证明a\equiv a^{k\varphi(n)+1}(\mod n)
设n=pq,a是某一个整数、gcd(a,n)=1且a不能被n整除,试证明a≡akφ(n)+1(modn)
若 a 与 n 不互质,必有 p ∣ a ( a 能被 p 整除 ) 或者 q ∣ a 。设 p ∣ a 成立,必有 g c d ( q , a ) = 1 ,否则 n ∣ a ,不符合题设条件。 同理设 q ∣ a 成立也是一样的情况,不失一般性,设 p ∣ a 成立。由欧拉定理和 φ ( n ) = ( p − 1 ) ( q − 1 ) 得到: a φ ( n ) ≡ 1 ( m o d q ) a k φ ( n ) ≡ 1 ( m o d q ) 令 m 为整数 , 有 a k φ ( n ) = m q + 1 a k φ ( n ) + 1 = m a q + a 将 a 分解为 a = x p a k φ ( n ) + 1 = m x p q + a = m x n + a 则 a k φ ( n ) + 1 ≡ a ( m o d n ) 成立 若a与n不互质,必有p|a(a能被p整除)或者q|a。设p|a成立,必有gcd(q,a)=1,否则n|a,不符合题设条件。\\同理设q|a成立也是一样的情况,不失一般性,设p|a成立。 由欧拉定理和\varphi(n)=(p-1)(q-1)得到:\\ a^{\varphi(n)}\equiv 1(\mod q) \\ a^{k\varphi(n)}\equiv 1(\mod q) \\ 令m为整数,有\\ a^{k\varphi(n)}=mq+1\\ a^{k\varphi(n) + 1}=maq+a\\ 将a分解为a=xp \\ a^{k\varphi(n) + 1}=mxpq+a=mxn+a\\ 则a^{k\varphi(n) + 1}\equiv a(\mod n)成立 若a与n不互质,必有p∣a(a能被p整除)或者q∣a。设p∣a成立,必有gcd(q,a)=1,否则n∣a,不符合题设条件。同理设q∣a成立也是一样的情况,不失一般性,设p∣a成立。由欧拉定理和φ(n)=(p−1)(q−1)得到:aφ(n)≡1(modq)akφ(n)≡1(modq)令m为整数,有akφ(n)=mq+1akφ(n)+1=maq+a将a分解为a=xpakφ(n)+1=mxpq+a=mxn+a则akφ(n)+1≡a(modn)成立文章来源:https://www.toymoban.com/news/detail-422436.html
参考资料:RSA解密正确性证明文章来源地址https://www.toymoban.com/news/detail-422436.html
到了这里,关于RSA算法加解密过程全解析的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!