目录
Kruskal算法
Kruskal重构树
在学习重构树之前,我们要先熟悉一下基本的kruskal算法
Kruskal算法
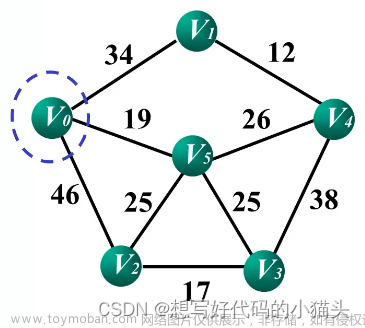
首先给出一张有向图,让我们求最小生成树(用总权值最小的一些边的集合,使得所有点都能互通,很明显n个点会有n-1条边)

kruskal算法思想是先把所有的边按权值大小排序,得到这个样子

然后从小往大依次取边,如果加上这条边和之前的边构成了环,就舍弃这条边,不然就加上,直至取得n-1条边,构成一棵树
例如此图,我们按照权值加完前四条边

在加入第五条边时,我们发现原图出现了环,我们就舍弃这条边

就这样一直加边,直至构成一棵完整的树

这就是kruskal算法的
Kruskal重构树
那么什么又是kruskal重构树呢?
kruskal重构树其实就是把这张图重建成一个二叉树,原图中所有的叶子节点都为原图中的点
其他点都有一个点权w,代表从左集合到右集合的路径,由于重构树是在kruskal的基础上完成的,所以我们必然可以得到一个自下而上点权不降的二叉树
比如我们还用上图距离,建一颗重构树
首先我们合并6,7两个集合,把他们两个连接到一个虚点上,该点权值为他们的边权

(红色代表虚点,白色代表原图的点)
然后我们依次2-8 , 5-6

就这样把这颗二叉树建完

最后重构树大概长这样
这棵树有很多独特的性质
就比如我们想知道从节点2到7路径的最大边权是多少,其实就是他们公共祖先这个虚点的点权值
再比如我们想知道从某个点出发,给出一个值,在通过所有边的权值都小于等于这个值时,我们走过多少个点,其实就等于这个点一直往上面找,找到最后一个小于等于这个值的虚点,他的子树的点我们都是可以通过的(因为从上到下点权不上升)
以上这种问题我们都可以通过在重构树上倍增的方式,把时间复杂度压到logn
典型例题有洛谷的P2245 星际导航 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
和去年icpc上海区域赛的H Problem - H - Codeforces
重构树板子:
int n, m;
int k, T, S, D;
struct edge
{
int a, b, w;
bool operator <(const edge& ee)const { return w < ee.w; }
}ed[M];
vector<int> e[N];//即为重构树
int d[N];
int p[N];
int a[N];
int down[N];
int fa[N][18];
int find(int x) {
return p[x] == x ? p[x] : p[x] = find(p[x]);
}
int kruskal() {
sort(ed + 1, ed + 1 + m);
fer(i, 1, 2*n)p[i] = i;
int cnt = n;
fer(i, 1, m) {
int a = find(ed[i].a), b = find(ed[i].b);
if (a^b){
d[++cnt]=ed[i].w;
p[a]=p[b]=cnt;
e[cnt].push_back(a);
e[cnt].push_back(b);
}
}
return cnt;
}
文章来源地址https://www.toymoban.com/news/detail-422661.html
文章来源:https://www.toymoban.com/news/detail-422661.html
到了这里,关于Kruskal重构树详解的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!