RSA密码原理详解及算法实现(六步即可掌握)

一、RSA算法概述

rsa算法是一种非对称加密算法，其安全性是建立在大素数难以分解的基础上的，即将两个大素数相乘十分容易，但想对其乘积进行分解却很困难，所以可以将其乘积公开作为加密密钥

二、RSA算法设计理念

根据数论，寻求两个大素数比较简单，而将它们的乘积进行因式分解却极其困难，因此可以将乘积公开作为加密密钥

三、加解密过程及密钥生成

1、加解密过程

此处从明文和密文加密和解密开始，然后讲密钥的生成

(1). 对于明文M，则有密文C=M^e mod n  (获得密文是明文的e次方再模n，即求余数)    

(2). 对于密文C，则有明文M=C^d mod n   (获得明文是密文的d次方再模n，即求余数)

明文和密文的产生是建立在一对密钥的基础上的，即(e,n)和(d,n) ,(e,n)称为公钥 , (d,n)称为私钥   (先记下公钥和私钥的概念，有个印象)

下面是一个形象的例子

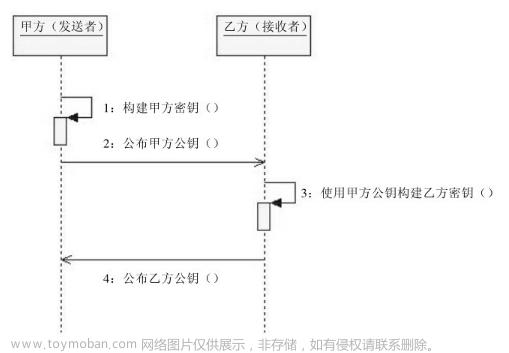
假设A要与B通信：

 A————————————————————————————B

(e,n)                                                                                             (d,n)

A握着（e,n）对想发送的明文M加密C=M^e mod n形成密文C，再将C发送给B

B拿到密文C，再用自己的私钥（d,n）对密文C解密还原明文M

现在我们只需要知道(e,n)和(d,n)即（e，d，n）三个密钥怎么来的就搞定了RSA算法

2、密钥生成过程  (e,d,n)

(1).求n

准备两个素数p，q（最好准备较大的素数）   (注:素数 质数是同一个东东)

n=p*q

至此n得到了

(2).根据第一步准备的p和q计算 n的欧拉函数φ(n)

φ(n)=(p-1)*(q-1)

(3).选取公钥e

选取条件：质数，1<e<φ(n)  ,  (e,φ(n))=1(e与φ(n)互质)

至此e得到了，在实际应用中，e一般为65537，(ctfer应该比较敏感吧hhh

(4).计算私钥d，计算e对于φ(n)的模反元素d。

d应满足：ed ≡ 1 (mod φ(n))             （即 （d*e）mod φ(n)=1）

至此(e,d,n)全部得出

带具体例子的视频在这里：

数学不好也能听懂的算法 - RSA加密和解密原理和过程_哔哩哔哩_bilibili

安全性推荐看这篇，此处不讲了，因为本文主要内容只是给大家讲解原理

python实现RSA算法-Python教程-PHP中文网

四、python实现

明白了算法的原理，代码实现也就变的简单了

具体思路就是，按照p，q得到密钥e，d，n后，执行加密和解密的式子。

import random


'''
Euclid's algorithm for determining the greatest common divisor
Use iteration to make it faster for larger integers
'''


def gcd(a, b):
    while b != 0:
        a, b = b, a % b
    return a


'''
Euclid's extended algorithm for finding the multiplicative inverse of two numbers
'''


def multiplicative_inverse(e, phi):
    d = 0
    x1 = 0
    x2 = 1
    y1 = 1
    temp_phi = phi

    while e > 0:
        temp1 = temp_phi//e
        temp2 = temp_phi - temp1 * e
        temp_phi = e
        e = temp2

        x = x2 - temp1 * x1
        y = d - temp1 * y1

        x2 = x1
        x1 = x
        d = y1
        y1 = y

    if temp_phi == 1:
        return d + phi


'''
Tests to see if a number is prime.
'''


def is_prime(num):
    if num == 2:
        return True
    if num < 2 or num % 2 == 0:
        return False
    for n in range(3, int(num**0.5)+2, 2):
        if num % n == 0:
            return False
    return True


def generate_key_pair(p, q):
    if not (is_prime(p) and is_prime(q)):
        raise ValueError('Both numbers must be prime.')
    elif p == q:
        raise ValueError('p and q cannot be equal')
    # n = pq
    n = p * q

    # Phi is the totient of n
    phi = (p-1) * (q-1)

    # Choose an integer e such that e and phi(n) are coprime
    e = random.randrange(1, phi)

    # Use Euclid's Algorithm to verify that e and phi(n) are coprime
    g = gcd(e, phi)
    while g != 1:
        e = random.randrange(1, phi)
        g = gcd(e, phi)

    # Use Extended Euclid's Algorithm to generate the private key
    d = multiplicative_inverse(e, phi)

    # Return public and private key_pair
    # Public key is (e, n) and private key is (d, n)
    return ((e, n), (d, n))


def encrypt(pk, plaintext):
    # Unpack the key into it's components
    key, n = pk
    # Convert each letter in the plaintext to numbers based on the character using a^b mod m
    cipher = [pow(ord(char), key, n) for char in plaintext]
    # Return the array of bytes
    return cipher


def decrypt(pk, ciphertext):
    # Unpack the key into its components
    key, n = pk
    # Generate the plaintext based on the ciphertext and key using a^b mod m
    aux = [str(pow(char, key, n)) for char in ciphertext]
    # Return the array of bytes as a string
    plain = [chr(int(char2)) for char2 in aux]
    return ''.join(plain)


if __name__ == '__main__':
    '''
    Detect if the script is being run directly by the user
    '''
    print("===========================================================================================================")
    print("================================== RSA Encryptor / Decrypter ==============================================")
    print(" ")

    p = int(input(" - Enter a prime number (17, 19, 23, etc): "))
    q = int(input(" - Enter another prime number (Not one you entered above): "))

    print(" - Generating your public / private key-pairs now . . .")

    public, private = generate_key_pair(p, q)

    print(" - Your public key is ", public, " and your private key is ", private)

    message = input(" - Enter a message to encrypt with your public key: ")
    encrypted_msg = encrypt(public, message)

    print(" - Your encrypted message is: ", ''.join(map(lambda x: str(x), encrypted_msg)))
    print(" - Decrypting message with private key ", private, " . . .")
    print(" - Your message is: ", decrypt(private, encrypted_msg))

    print(" ")
    print("============================================ END ==========================================================")
    print("===========================================================================================================")

懒得写了，git上co的)文章来源地址https://www.toymoban.com/news/detail-422794.html

到了这里，关于RSA密码原理详解及算法实现(六步即可掌握)的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！