前言
本文内容源于对《数据结构(C语言版)》(第2版)、王道讲解学习所得心得、笔记整理和总结,以便复习。
可搭配以下链接一起学习:
【考研】《数据结构》知识点总结.pdf_考研数据结构知识点总结-其它文档类资源-CSDN文库
【2023考研】数据结构常考应用典型例题(含真题)_住在阳光的心里的博客-CSDN博客
目录
前言
一、基本概念
二、KMP算法
三、KMP算法的进一步优化
四、习题
一、基本概念
1、串的模式匹配:子串(即模式串)的定位操作,即求子串在主串中的位置。
例1:设有两个串S1 和串S2 ,求 S2 在 S1 中首次出现的位置的运算称为模式匹配。
2、字符串的前缀、后缀和部分匹配值
(1)前缀:除最后一个字符以外,字符串的所有头部子串。
(2)后缀:除第一个字符以外,字符串的所有尾部子串。
(3)部分匹配值:字符串的前缀和后缀的最长相等前后缀长度。
例2:以 ‘ ababa ’ 为例:
| 串 | 前缀 | 后缀 | 前后缀交集 | 最长相等前后缀长度 |
| ‘ a ’ | 空集 | 空集 | 空集 | 0 |
| ‘ ab ’ | { a } | { b } | 空集 | 0 |
| ‘ aba ’ | { a, ab } | { a, ba } | { a } | 1 |
| ‘ abab ’ | { a, ab, aba } | { b, ab, bab } | { ab } | 2 |
| ‘ ababa ’ | { a, ab, aba, abab } | { a, ba, aba, baba } | { aba } | 3 |
所以,串 S 的 ‘ ababa ’ 的部分匹配值为 00123,部分匹配值(Partial Match,PM)的表如下:
| 编号 | 1 | 2 | 3 | 4 | 5 |
| S | a | b | a | b | a |
| PM | 0 | 0 | 1 | 2 | 3 |
二、KMP算法
已知:右移位数 = 已匹配的字符数 - 对应的部分匹配值
写成:Move = (j - 1) - PM[j - 1]
针对例 2 ,PM 表右移一位,得到 next 数组:
| 编号 | 1 | 2 | 3 | 4 | 5 |
| S | a | b | a | b | a |
| next | -1 | 0 | 0 | 1 | 2 |
改写成:Move = (j - 1) - next[j]
相当于将子串的比较指针回退到 j = j - Move = next[j] + 1,
为了使公式更简洁,将 next 数组整体加1:
| 编号 | 1 | 2 | 3 | 4 | 5 |
| S | a | b | a | b | a |
| next | 0 | 1 | 1 | 2 | 3 |
即子串指针变化公式为 j = next[j]。
在实际匹配过程中,子串在内存里是不会移动的,而是指针在变化。
next[j] 的含义:在子串的第 j 个字符与主串发生失配时,则跳到子串的 next[j] 位置重新与主串当前位置进行比较。
当模式串第一个字符 (j = 1) 与主串第 i 个字符发生失配时,规定 next[1] = 0。将模式串右移一位,从主串的下一个位置 (i + 1) 和模式串的第一个字符继续比较。
例3:求模式串的 next 值:
| j | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 模式 | a | b | a | a | b | c | a | b | a |
| next[j] | 0 | 1 | 1 | 2 | 2 | 3 | ? | ? | ? |
上表中,已求得6个字符的 next 值,现求 next[7]。
解法一:(选择题中常用方法)
‘a',最长相等前后缀长度为 0
’ab',最长相等前后缀长度为 0
'aba',最长相等前后缀长度为 1
'abaa',最长相等前后缀长度为 1
'abaab',最长相等前后缀长度为 2
'abaabc',最长相等前后缀长度为 0
'abaabca',最长相等前后缀长度为 1
'abaabcab',最长相等前后缀长度为 2
'abaabcaba' ,最长相等前后缀长度为 3
串 S 的 'abaabcaca' 的部分匹配值为 0 0 1 1 2 0 1 2 3
PM 表右移一位,得到 next 数组:-1 0 0 1 1 2 0 1 2
next 数组整体加1:0 1 1 2 2 3 1 2 3
由此可知,next[7] = 1; next[8] = 2; next[9] = 3;
解法二:
关键点:若 , 则 next[j+1] = next[j] + 1,否则令 j = next[j],继续比较
因为 next[6] = 3,又 ,则需比较 和 (因 next[3] = 1),
由于 而 next[1] = 0,所以 next[7] = 1;
求 next[8],因 ,则 next[8] = next[7] + 1 = 2;
求 next[9],因 ,则 next[9] = 3。
求 next 值的程序如下:
void get_next (String T, int next []) {
int i,j = 0;
next = 0;
while(i < T.length){
if(j == 0 || T.ch[i] == T.ch[j]){
++i;
++j;
next[i] = j; //若pi = pj, 则 next[j+1] = next[j] + 1
}
else{
j = next[j]; //否则令 j = next[j], 循环继续
}
}
}KMP的匹配算法:
与 next 数组的求解相比,KMP的匹配算法相对要简单很多,它在形式上与简单的模式匹配算法很相似。不同之处仅在于当匹配过程产生失配时,指针 i 不变,指针 j 退回到 next[j] 的位置并重新进行比较,并且当指针 j 为 0 时,指针 i 和 j 同时加1。
即若主串的第 i 个位置和模式串的第一个字符不等,则应从主串的第 i + 1 个位置开始匹配。
具体代码如下:
int Index_KMP(String S, String T, int next[]){
int i = 1, j = 1;
while (i <= S.length && j <= T.length){
if(j == 0 || S.ch[i] == T.ch[j]){ //继续比较后继字符
++i;
++j;
}
else{
j = next[j]; //模式串向右移动
}
}
if (j > T.length)
return i - T.length; //匹配成功
else
return 0;
}
时间复杂度为 O(m + n)。
【注意】尽管普通模式匹配的时间复杂度是O(mn),KMP算法的时间复杂度是O(m + n),但在一般情况下,普通模式匹配的实际执行时间近似为O(m + n),因此至今仍被采用。
KMP算法仅在主串与子串有很多 “ 部分匹配 ” 时才显得比普通算法快得多,其主要优点是主串不回溯。
三、KMP算法的进一步优化
更新后的数组命名为 nextval,计算 next 数组修正值的算法如下,此时匹配算法不变。
void get_nextval (String T,int nextval[]){
int i = 1, j = 0;
nextval[1] = 0;
while(i < T.length){
if(j == 0 || T.ch[i] == T.ch[j]){
++i;
++j;
if(T.ch[i] != T.ch[j])
nextvall[i] = j;
else
nextval[i] = nextval[j];
else
j = nextval[j];
}
}nextval 详细的手动计算方式请见习题 2 。
四、习题
1、KMP 算法的特点是在模式匹配时指示主串的指针( B )
A. 不会变大 B. 不会变小 C.都有可能 D. 无法判断
解:在 KMP 算法的比较过程,主串不会回溯,所以主串的指针不会变小。
2、串 'ababaaababaa' 的 nextval 数组为( C )。
A. 0,1, 0,1, 1, 2, 0,1, 0, 1, 0, 2 B. 0, 1, 0, 1, 1, 4, 1, 1, 0, 1, 0, 2
C. 0,1, 0,1, 0, 4, 2,1, 0, 1, 0, 4 D. 0, 1, 1, 1, 0, 2, 1, 1, 0, 1, 0, 4
解:【注意】如果串的位序是从 1 开始的,则 next 数组需要整体加1,若串的位序从 0 开始,则 next 数组不需要整体加 1。
由选项可知,nextval 数组由 0 开始,因为 nextval[1] = 0,可知串的位序从 1 开始。
(1)求 next 数组:
'a',最长相等前后缀长度为 0
'ab',最长相等前后缀长度为 0
'aba',最长相等前后缀长度为 1
'abab',最长相等前后缀长度为 2
'ababa',最长相等前后缀长度为 3
'ababaa',最长相等前后缀长度为 1
'ababaaa',最长相等前后缀长度为 1
'ababaaab',最长相等前后缀长度为 2
'ababaaaba',最长相等前后缀长度为 3
'ababaaabab',最长相等前后缀长度为 4
'ababaaababa',最长相等前后缀长度为 5
'ababaaababaa',最长相等前后缀长度为 6
串 S 的 'abaabcaca' 的部分匹配值为 0 0 1 2 3 1 1 2 3 4 5 6
PM 表右移一位,得到 next 数组:-1 0 0 1 2 3 1 1 2 3 4 5
因为串的位序是从 1 开始的,所以 next 数组整体加 1:0 1 1 2 3 4 2 2 3 4 5 6
(2)求 nextval 数组:
得出串 S = 'ababaaababaa' 的 next 数组后,有下表:
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| S | a | b | a | b | a | a | a | b | a | b | a | a |
| next | 0 | 1 | 1 | 2 | 3 | 4 | 2 | 2 | 3 | 4 | 5 | 6 |
| nextval | 0 |
从 j = 2 开始,依次判断 ,是否等于 ?
不相等:nextval[j] = next[j]
相等:将 next[j] 修正为 next[next[j]],直至两者不相等为止。
步骤1:令 nextval[1] = next[1] = 0
步骤2:j = 2, next[j] = next[2] = 1, 则 p2 = b ≠ p1 = a,nextval[2] = next[2] = 1
步骤3:j = 3, next[j] = next[3] = 1, 则 p3 = p1 = a,则 nextval[3] = nextval[next[3]] = nextval[1] = 0
步骤4:j = 4, next[j] = next[4] = 2, 则 p4 = p2 = b,则 nextval[4] = nextval[next[4]] = nextval[2] = 1
步骤5:j = 5, next[j] = next[5] = 3, 则 p5 = p3 = a,则 nextval[5] = nextval[next[5]] = nextval[3] = 0
步骤6:j = 6, next[j] = next[6] = 4, 则 p6 = a ≠ p4 = b,则 nextval[6] = next[6] = 4
步骤7:j = 7, next[j] = next[7] = 2, 则 p7 = a ≠ p2 = b,则 nextval[6] = next[7] = 2
步骤8:j = 8, next[j] = next8] = 2, 则 p8 = p2 = b,则 nextval[8] = nextval[next[8]] = nextval[2] = 1
步骤9:j = 9, next[j] = next[9] = 3, 则 p9 = p3 = a,则 nextval[9] = nextval[next[9]] = nextval[3] = 0
步骤10:j=10, next[10] = 4, 则 p10 = p4 = b,则 nextval[10] = nextval[next[10]] = nextval[4] = 1
步骤11:j=11, next[11] = 5, 则 p11 = p5 = a,则 nextval[11] = nextval[next[11]] = nextval[5] = 0
步骤12:j=12, next[12] = 6, 则 p12 = p6 = a,则 nextval[12] = nextval[next[12]] = nextval[6] = 4
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| S | a | b | a | b | a | a | a | b | a | b | a | a |
| next | 0 | 1 | 1 | 2 | 3 | 4 | 2 | 2 | 3 | 4 | 5 | 6 |
| nextval | 0 | 1 | 0 | 1 | 0 | 4 | 2 | 1 | 0 | 1 | 0 | 4 |
串 'ababaaababaa' 的 nextval 数组为 0 1 0 1 0 4 2 1 0 1 0 4
由上述推理可知,答案选C。
【注意】
在步骤 5 的推理中, ,按前面的讲解部分,应该继续让 和 比较,(恰好 ),注意到此时 nextval[3] 的值已存在,故直接将 nextval[5]赋值为 nextval[3]。
对于一般情况,nextval 数组是从前往后逐步求解的,
发生 时,因为 nextval[next[j]] 早已求得,
所以直接将 nextval[j] 赋值为 nextval[next[j]]。
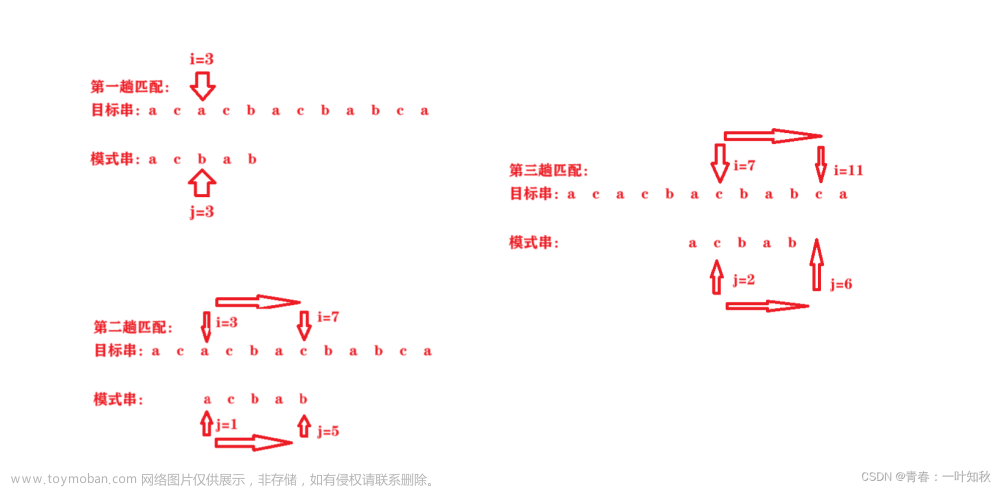
3、【2015统考真题】已知字符串 S 为 'abaabaabacacaabaabcc',模式串 t 为' abaabc',采用 KMP 算法进行匹配,第一次出现“失配” (s[i] ≠ t[j]) 时,i = j = 5, 则下次开始匹配时,i 和 j 的值分别是( C )
A. i = 1, j = 0 B. i = 5, j = 0
C. i = 5, j = 2 D. i = 6, j = 2
解: KMP的匹配算法在于当匹配过程产生失配时,指针 i 不变,指针 j 退回到 next[j] 的位置并重新进行比较,并且当指针 j 为 0 时,指针 i 和 j 同时加1。
所以, i = 5,j = next[j] = next[5],关键是求 next 数组
由题知,主串和模式串的位序都是从 0 开始的,将PM右移一位后得到 next 数组:
| 编号 | 0 | 1 | 2 | 3 | 4 | 5 |
| 模式串 t | a | b | a | a | b | c |
| PM | 0 | 0 | 1 | 1 | 2 | 0 |
| next | -1 | 0 | 0 | 1 | 1 | 2 |
由上表知 next[5] = 2,即 j = 2。
4、【2019统考真题】设主串T = ' abaabaabcabaabc ', 模式串 s = 'abaabc', 采用 KMP 算法进行模式匹配,到匹配成功时为止,在匹配过程中进行的单个字符间的比较次数是( B )。
A. 9 B. 10 C.12 D. 15
解:模式串 s = 'abaabc',最长相等前后缀长度有:
‘a',最长相等前后缀长度为 0
‘ab',最长相等前后缀长度为 0
‘aba',最长相等前后缀长度为 1
‘abaa',最长相等前后缀长度为 1
‘abaab',最长相等前后缀长度为 2
‘abaabc',最长相等前后缀长度为 0
所以,模式串 s = 'abaabc' 的部分匹配值 PM 为 001120
将 PM 右移一位,得 next 数组为 -1 0 0 1 1 2,即如下表:
| 编号 | 0 | 1 | 2 | 3 | 4 | 5 |
| s | a | b | a | a | b | c |
| next | -1 | 0 | 0 | 1 | 1 | 2 |
【注意】如果串的位序是从 1 开始的,则 next 数组需要整体加1,若串的位序从 0 开始,则 next 数组不需要整体加 1。
| 编号 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 主串 | a | b | a | a | b | a | a | b | c | a | b | a | a | b | c |
| 第一趟 | a | b | a | a | b | c | |||||||||
| 失败, 比较了6次 |
|||||||||||||||
| 第二趟 | a | b | a | a | b | c | |||||||||
| 开始比较 | 成功, 比较了4次 |
第一趟连续比较 6 次,在模式串的 5 号位和主串的 5 号位匹配失败,模式串的下一个比较位置为 next[5] = 2,即下一次比较从模式串的 2 号位和主串的 5 号位开始,然后直到模式串 5 号位和主串8 号位匹配,第二趟比较 4 次,模式串匹配成功。文章来源:https://www.toymoban.com/news/detail-423061.html
单个字符的比较次数为10次,因此选B。文章来源地址https://www.toymoban.com/news/detail-423061.html
到了这里,关于【考研】串的模式匹配算法——KMP算法(含真题)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!





![[入门必看]数据结构4.2:串的模式匹配](https://imgs.yssmx.com/Uploads/2024/02/422466-1.png)