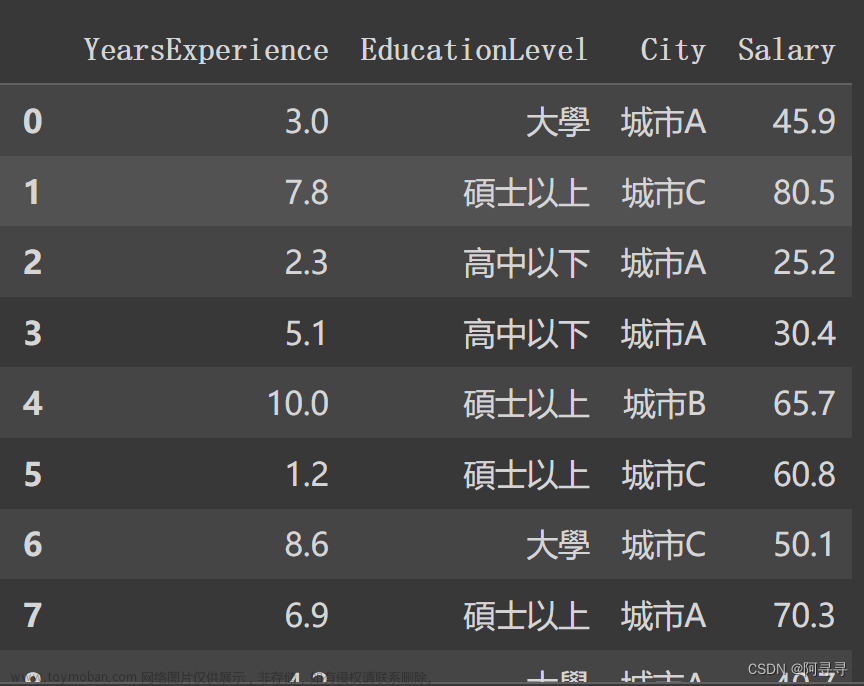
前言
什么是多元线性回归分析预测法
在市场的经济活动中,经常会遇到某一市场现象的发展和变化取决于几个影响因素的情况,也就是一个因变量和几个自变量有依存关系的情况。而且有时几个影响因素主次难以区分,或者有的因素虽属次要,但也不能略去其作用。例如,某一商品的销售量既与人口的增长变化有关,也与商品价格变化有关。这时采用一元回归分析预测法进行预测是难以奏效的,需要采用多元回归分析预测法。
多元回归分析预测法,是指通过对两个或两个以上的自变量与一个因变量的相关分析,建立预测模型进行预测的方法。当自变量与因变量之间存在线性关系时,称为多元线性回归分析。
一、多元线性回归
一元线性回归是一个主要影响因素作为自变量来解释因变量的变化,但是在现实问题研究中,因变量的变化往往受几个重要因素的影响,此时就需要用两个或两个以上的影响因素作为自变量来解释因变量的变化,这就是多元回归亦称多重回归。当多个自变量与因变量之间是线性关系时,所进行的回归分析就是多元线性回归。
设y为因变量,  为自变量,并且自变量与因变量之间为线性关系时,则多元线性回归模型为:
为自变量,并且自变量与因变量之间为线性关系时,则多元线性回归模型为:
其中,b0为常数项, 为回归系数,b1为
为回归系数,b1为  固定时,x1 每增加一个单位对 y 的效应,即 x1 对 y 的偏回归系数;同理 b2 为 x1, xk 固定时,x2每增加一个单位对y的效应,故有 x2 对 y 的偏回归系数。如果两个自变量 x1,x2 同一个因变量y呈线性相关时,可用二元线性回归模型描述为:
固定时,x1 每增加一个单位对 y 的效应,即 x1 对 y 的偏回归系数;同理 b2 为 x1, xk 固定时,x2每增加一个单位对y的效应,故有 x2 对 y 的偏回归系数。如果两个自变量 x1,x2 同一个因变量y呈线性相关时,可用二元线性回归模型描述为:
在建立多元性回归模型时,为了保证回归模型具有优秀的解释能力和预测效果,应首先注意自变量的选择,其准则是:
-
(1)自变量对因变量必须有显著的影响,并呈密切的线性相关;
-
(2)自变量与因变量之间的线性相关必须是真实的,而不是形式上的;
-
(3)自变量之间具有一定的互斥性,即自变量之间的相关程度不能高于自变量与因变量之间的相关程度;
-
(4)自变量应具有完整的统计数据,其预测值容易确定。
多元性回归模型的参数估计,同一元线性回归方程一样,也是在要求误差平方和 为最小的前提下,用最小二乘法求解参数。
为最小的前提下,用最小二乘法求解参数。
用二元线性回归模型来求解回归参数的标准参数方程组为:
二、多元线性回归模型求解
多元线性回归模型的主要作用:(主要用于预测)通过建模来拟合我们所提供的或是收集到的这些因变量和自变量的数据,收集到的数据拟合之后来进行参数估计。参数估计的目的主要是来估计出模型的偏回归系数的值。估计出来之后就可以再去收集新的自变量的数据去进行预测,也称为样本量。
多元线性回归模型:
回归模型算法实现:
import pandas as pd
import numpy as np
import statsmodels.api as sm# 实现了类似于二元中的统计模型,比如ols普通最小二乘法
import statsmodels.stats.api as sms#实现了统计工具,比如t检验、F检验...
import statsmodels.formula.api as smf
import scipy
np.random.seed(991)# 随机数种子
# np.random.normal(loc=0.0, scale=1.0, size=None)
# loc:float 此概率分布的均值(对应着整个分布的中心),loc=0说明这一个以Y轴为对称轴的正态分布,
# scale:float 此概率分布的标准差(对应于分布的宽度,scale越大越矮胖,scale越小,越瘦高)
# size:int or tuple of ints 输出的shape,默认为None,只输出一个值
# 数据生成
x1 = np.random.normal(0,0.4,100)# 生成符合正态分布的随机数(均值为0,标准差0.4,所生成随机数的个数为100)
x2 = np.random.normal(0,0.6,100)
x3 = np.random.normal(0,0.2,100)
eps = np.random.normal(0,0.05,100)# 生成噪声数据,保证后面模拟所生成的因变量的数据比较接近实际的环境
X = np.c_[x1,x2,x3]# 调用c_函数来生成自变量的数据的矩阵,按照列进行生成的;100×3的矩阵
beta = [0.1,0.2,0.7]# 生成模拟数据时候的系数的值
y = np.dot(X,beta) + eps# 点积+噪声(dot是表示乘)
X_model = sm.add_constant(X)# add_constant给矩阵加上一列常量1,便于估计多元线性回归模型的截距,也是便于后面进行参数估计时的计算
model = sm.OLS(y,X_model)# 调用OLS普通最小二乘法来求解
# 下面是进行参数估计,参数估计的主要目的是估计出回归系数,根据参数估计结果来计算统计量,
# 这些统计量主要的目的就是对我们模型的有效性或是显著性水平来进行验证。
results = model.fit()# fit拟合
results.summary()# summary方法主要是为了显示拟合的结果
OLS 回归结果:
2.1最小二乘法实现参数估计—估计自变量X的系数
回归系数的计算:X转置(T)乘以X,对点积求逆后,再点乘X转置,最后点乘y 。
beta_hat = np.dot(np.dot(np.linalg.inv(np.dot(X_model.T,X_model)),X_model.T),y)# 回归系数
print('回归系数:',np.round(beta_hat,4))# 四舍五入取小数点后4位
print('回归方程:Y_hat=%0.4f+%0.4f*X1+%0.4f*X2+%0.4f*X3' % (beta_hat[0],beta_hat[1],beta_hat[2],beta_hat[3]))
输出为:
回归系数: [-0.0097 0.0746 0.2032 0.7461]
回归方程:Y_hat=-0.0097+0.0746*X1+0.2032*X2+0.7461*X3
代码讲解:
2.2决定系数:R² 与调整后 R²
决定系数R² 主要作用是:检验回归模型的显著性
# 因变量的回归值=np.dot(X_model,系数向量)
y_hat = np.dot(X_model,beta_hat)# 回归值(拟合值)的计算
y_mean = np.mean(y) # 求因变量的平均值
sst = sum((y-y_mean)**2) # 总平方和:即y减去y均值后差的平方和
ssr = sum((y_hat-y_mean)**2) # 回归平方和: y回归值减去y均值后差的平方和
sse = sum((y-y_hat)**2) # 残差平方和: y值减去y回归值之差的平方和
# sse = sum(results.resid**2) # 结果和上面注释了的式子一样,或许有小数点的误差,但基本上可忽略不计
R_squared =1 - sse/sst # R²:1减去残差平方和除以总平方和商的差;求解方法二:R²=ssr/sst
# 按照线性回归模型原理来说:[残差平方和+回归平方和=总平方和]→[R²=ssr/sst]
print('R²:',round(R_squared,3))
# 调整后平方和:100表示样本数据总数(n),3表示自变量个数(p)
adjR_squared =1- (sse/(100-3-1))/(sst/(100-1)) # 1-(残差的平方和/残差的自由度)/(总平方和/无偏估计),式子开头为常数-1
# 残差的自由度也是残差方差的无偏估计
print('调整后R²:',round(adjR_squared,3))
输出为:
R²: 0.931
调整后R²: 0.929
说明:
2.3F检验参数
F显著性检验:
F = (ssr/3)/(sse/(100-3-1));
print('F统计量:',round(F,1))
# 累积分布函数叫cdf(),调用方法和下面残差函数调用方法一样;注意:cdf+sf算出来的值为1
F_p = scipy.stats.f.sf(F,3,96)# 使用F分布的残存函数计算P值;sf是残存函数英语单词的缩写;3和96分别是两个自由度
print('F统计量的P值:', F_p)
输出为:
F统计量: 432.6
F统计量的P值: 1.2862966484214766e-55
说明:
- 若假设的检验的P值越小,表示的显著性水平就越高。也就是说拒绝原假设H0,接受备选假设H1。
2.4对数似然、AIC与BIC
# 对数似然值计算公式: L=-(n/2)*ln(2*pi)-(n/2)*ln(sse/n)-n/2;sse/n就是方差
res = results.resid# 残差(sse = sum(results.resid**2) 惨差平方和)
# 可以写成res = y-y_hat
sigma_res = np.std(res) # 残差标准差
var_res = np.var(res) # 残差方差
L = -(100/2)*np.log(2*np.pi)-(100/2)*np.log(var_res)-100/2
print('对数似然为:', round(ll,2))# 保留两位小数
# 赤池信息准则:-2乘以对数似然比+2*(参数个数+1)。
# −2ln(L)+2(p+1)(赤池弘次),其中p为参数个数,ln(L)即L
AIC = -2*L + 2*(3+1)
print('AIC为:',round(AIC,1))
# 贝叶斯信息准则:−2ln(L)+ln(n)∗(p+1),其中ln(L)即Lr
BIC = -2*L+np.log(100)*(3+1)
print('BIC为:',round(BIC,1))
输出为:
对数似然为: 152.69
AIC为: -297.4
BIC为: -287.0
- AIC和BIC越小越好。
2.5回归系数标准差
回归系数标准差为:
from scipy.stats import t,f
C = np.linalg.inv(np.dot(X_model.T,X_model))# X倒置点乘X,然后对点集求逆
C_diag = np.diag(C)# 取出C矩阵对角线的值
sigma_unb= (sse/(100-3-1))**(1/2)# 残差标准差的无偏估计:残差平方和/(样本数减参数个数减1)
'''
回归系数标准差std err的计算:
计算方式:残差标准差(无偏估计)乘以(C矩阵对角线上对应值的平方根)
'''
# 标准差
stdderr_const = sigma_unb*(C_diag[0]**(1/2))# 常数项(截距)的标准差,对应C_diag[0]
print('常数项(截距)的标准差:',round(stdderr_const,3))
stderr_x1 = sigma_unb*(C_diag[1]**(1/2))# 第一个系数对应C_diag[1]
print('beta1的标准差:',round(stderr_x1,3))
stderr_x2 = sigma_unb*(C_diag[2]**(1/2))# 第二个系数对应C_diag[2]
print('beta2的标准差:',round(stderr_x2,3))
stderr_x3 = sigma_unb*(C_diag[3]**(1/2))# 第三个系数对应C_diag[3]
print('beta3的标准差:',round(stderr_x3,3))
# 矩阵
print('C矩阵:\n', C)
print('\nC矩阵的对角线元素:',C_diag)
输出标准差为:
常数项(截距)的标准差: 0.005
beta1的标准差: 0.015
beta2的标准差: 0.009
beta3的标准差: 0.03
输出矩阵为:
C矩阵:
[[ 1.02054345e-02 1.95714789e-03 -8.54037508e-05 -6.90581790e-03]
[ 1.95714789e-03 7.92625905e-02 -3.13550686e-03 -3.64832485e-04]
[-8.54037508e-05 -3.13550686e-03 2.84951362e-02 -8.72645509e-03]
[-6.90581790e-03 -3.64832485e-04 -8.72645509e-03 3.05673367e-01]]
C矩阵的对角线元素: [0.01020543 0.07926259 0.02849514 0.30567337]
2.6回归系数的显著性t检验
回归系数显著性检验:
t_const = beta_hat[0]/stdderr_const
print('截距项的t值:',round(t_const,3))
p_const = 2*t.sf(t_const,96)
print("P>|t|:",round(p_const,3))
t_x1 = beta_hat[1]/stderr_x1
print('x1系数的t值:',round(t_x1,3))
p_t1 = 2*t.sf(t_x1,96)
print("P>|t|:",round(p_t1,3))
# t_x2 = beta_h
输出为:
截距项的t值: -1.798
P>|t|: 1.925
x1系数的t值: 4.941
P>|t|: 0.0
- t值足够小就可以认为回归方程的系数是具有显著性的,显著性水平是比较高的,否则就可以认为这个回归系数的显著性不高。
三、多元线性回归问题TensorFlow实践(波士顿房价预测)
数据下载方法:
- 波士顿房价数据
- 使用从sklearn库中导出数据集
首先需要用到sklearn里面的数据集以及调用pandas库
from sklearn import datasets
import pandas as pd
boston = datasets.load_boston()
再用pandas库中的DataFrame函数,这个函数可以指定data,columns,index等,若不指明columns,则每列数据的标签会以1、2、3等标记,这里我们每列数据的标签用数据集里面的。
data =pd.DataFrame(data=boston.data,columns=boston.feature_names)
print(data)
最后把数据导入csv文件中。
data.to_csv('./boston.csv', index=None)
- 原数据中有14列数据,由于data=pd.DataFrame(data=boston.data,columns=boston.feature_names) 这里的feature_names指的是特征的名字,也就是13个自变量,至于MEDV,你再用target即可(把boston.feature_names改成boston.target),而且运行boston.keys() 你也可以看到关于这个数据集的介绍(包括目标、特征、描述)
波士顿房价数据:
波士顿房价数据集包括506个样本,每个样本包括12个特征变量和该地区的平均房价。房价(单价)显然和多个特征变量相关,不是单变量线性回归(- 元线性回归)问题。选择多个特征变量来建立线性方程,这就是多变量线性回归(多 元线性回归)问题。
| 字段 | 字段说明 |
|---|---|
| CRIM | 城镇人均犯罪率 |
| ZN | 占地面积超过25,000平方英尺的住宅用地比例。 |
| INDUS | 每个城镇非零售业务的比例。 |
| CHAS | Charles River虚拟变量(如果是河道,则为1;否则为0) |
| NOX | 一氧化氮浓度(每千万份) |
| RM | 每间住宅的平均房间数 |
| AGE | 1940年以前建造的自住单位比例 |
| DIS | 加权距离波士顿的五个就业中心 |
| RAD | 径向高速公路的可达性指数 |
| TAX | 每10,000美元的全额物业税率 |
| PTRATIO | 城镇的学生与教师比例 |
| B | 1000(Bk - 0.63)^ 2其中Bk是城镇黑人的比例 |
| LSTAT | 人口状况下降% |
| MEDV | 自有住房的中位数报价, 单位1000美元 |
- 对波士顿房价数据用pandas来处理:
# import tensorflow as tf #导入Tensorflow
import tensorflow.compat.v1 as tf # 由于tensorflow对placeholder无法使用,所以引入tensorflow.compat.v1
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd # 能快速读取常规大小的文件。Pandas能提供高性能、易用的数据结构和数据分析工具
from sklearn.utils import shuffle # 随机打乱工具,将原有序列打乱,返回一个全新的顺序错乱的值
#读取数据文件,结果为DataFrame格式
df_data = pd.read_csv('boston.csv')
df_data

对于下载tensorflow 可以参考这篇文章:Win10下用Anaconda安装TensorFlow 按照里面所有步骤完成后还是用不了tensorflow 的话,就在Anaconda Prompt中启动tensorflow环境并进入ipython环境中,再次下载:
# pip install tf
pip install tensorflow
就可以使用了。
df_data.head(3) # 显示前3条数据

- 数据准备(相关操作)
# 获取数据集的值
ds=df_data.values # d f.values以np.array形式返回数据集的值
print(ds.shape) # 查看数据的形状
输出为:(506, 13)
print(ds) # 查看数据集的值
输出为:
- 划分特征数据和标签数据
# x_data 为归一化前的前12列特征数据
x_data = ds[:,:12]
# y_data 为最后1列标签数据
y_data = ds[:,12]
print('x_data shape=',x_data.shape)
print('y_data shape=',y_data.shape)
输出为:
- 特征数据归一化
#对特征数据{0到11}列 做(0-1)归一化
for i in range(12):
df[:,i] = (df[:,i]-df[:,i].min())/(df[:,i].max()-df[:,i].min())
df

- 模型定义
5.1 定义特征数据和标签数据的占位符
#shape中None表示行的数量未知,在实际训练时决定一次带入多少行样本,从一个样本的随机SDG到批量SDG都可以
x = tf.placeholder(tf.float32,[None,12],name = "X") #12个特征数据(12列)
y = tf.placeholder(tf.float32,[None,1],name = "Y") #1个标签数据(1列)
5.2 定义模型函数
#定义了一个命名空间.
#命名空间name_scope,Tensoflow计算图模型中常有数以千计节点,在可视化过程中很难一下子全部展示出来
# 因此可用name_scope为变量划分范围,在可视化中,这表示在计算图中的一个层级
with tf.name_scope("Model"):
# w 初始化值为shape=(12,1)的随机数
w = tf.Variable(tf.random_normal([12,1],stddev=0.01),name="W")
# b 初始化值为1.0
b = tf.Variable(1.0,name="b")
# w和x是矩阵相乘,用matmul,不能用mutiply或者*
def model(x,w,b):
return tf.matmul(x,w) + b
#预测计算操作,前向计算节点
pred = model(x,w,b)
- 模型训练
6.1 设置训练超参数
#迭代轮次
train_epochs = 50
#学习率
learning_rate = 0.01
6.2 定义均方差损失函数
#定义损失函数
with tf.name_scope("LossFunction"):
loss_function = tf.reduce_mean(tf.pow(y-pred,2)) #均方误差
6.3 创建优化器
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss_function)
6.4 会话
#声明会话
sess = tf.Session()
#定义初始化变量的操作
init = tf.global_variables_initializer()
#启动会话
sess.run(init)
6.5 训练
#迭代训练
for epoch in range(train_epochs):
loss_sum = 0.0
for xs,ys in zip(x_data,y_data):
xs = xs.reshape(1,12)
ys = ys.reshape(1,1)
#feed数据必须和Placeholder的shape一致
_,loss = sess.run([optimizer,loss_function],feed_dict={x:xs,y:ys})
loss_sum = loss_sum + loss
#打乱数据顺序,防止按原次序假性训练输出
x_data,y_data = shuffle(x_data,y_data)
b0temp = b.eval(session=sess) #训练中当前变量b值
w0temp = w.eval(session=sess) #训练中当前权重w值
loss_average = loss_sum/len(y_data) #当前训练中的平均损失
print("epoch=",epoch+1,"loss=",loss_average,"b=",b0temp,"w=",w0temp)
输出为:
epoch= 1 loss= 28.082918898316105 b= 3.952297 w= [[ 0.51253736]
[-0.9672818 ]
[ 2.1312068 ]
[-0.21723996]
[ 1.6660578 ]
[-1.8813397 ]
[ 4.6080937 ]
[ 0.3415178 ]
[ 0.8034863 ]
[ 1.5301441 ]
[ 2.754847 ]
[ 1.4393961 ]]
epoch= 2 loss= 26.376526752740993 b= 4.887504 w= [[ 1.5641255 ]
[-1.1011099 ]
[ 3.9318624 ]
[-0.53754747]
[ 3.4213843 ]
[-4.5665426 ]
[ 7.1060243 ]
[ 0.17595242]
[ 1.6169361 ]
[ 2.7584982 ]
[ 3.626495 ]
[ 0.01978375]]
epoch= 3 loss= 24.173813558376537 b= 5.395661 w= [[ 2.1237833 ]
[-0.54208773]
[ 3.853566 ]
[-1.1139921 ]
[ 3.4763796 ]
[-6.7673526 ]
[ 7.363592 ]
[ 0.9175515 ]
[ 0.79786545]
[ 2.145488 ]
[ 3.542476 ]
[-0.7713235 ]]
... ...后面还有47条数据就不展示。
- 模型应用
n = np.random.randint(506) # 随机确定一条来看看效果
print(n)
x_test = x_data[n]
x_test = x_test.reshape(1,12)
predict = sess.run(pred,feed_dict={x:x_test})
print("预测值:%f"%predict)
target = y_data[n]
print("标签值:%f"%target)
输出为:
进一步可视化:
-
根据波士顿房价信息进行预测,多元线性回归+特征数据归一化+可视化
添加loos_list值列表,并且输出可视化plt.plot(loss_list)
输出为:
-
根据波士顿房价信息进行预测,多元线性回归+特征数据归一化+可视化+TensorBoard可视化
TensorBoard可视化准备数据
#设置日志存储目录
logdir='d:/log'
#创建一个操作,用于记录损失值loss,后面在TensorBoard中SCALARS栏可见
sum_loss_op = tf.summary.scalar("loss",loss_function)
#把所有需要记录摘要日志文件的合并,方便一次性写入
merged = tf.summary.merge_all()
输出为:
总结
对于数据集划分还可以继续优化:
划分数据集的方法:
一种方法是将数据集分成两个子集:
- 训练集 - 用于训练模型的子集
- 测试集 - 用于测试模型的子集
通常,在测试集上表现是否良好是衡量能否在新数据上表现良好的有用指标,前提是:
测试集足够大,不会反复使用相同的测试集来作假。
拆分数据:将单个数据集拆分为一个训练集和一个测试集
确保测试集满足以下两个条件:
- (1)规模足够大,可产生具有统计意义的结果
- (2)能代表整个数据集,测试集的特征应该与训练集的特征相同
但是在每次迭代时,都会对训练数据进行训练并评估测试数据,并以基于测试数据的评估结果为指导来选择和更改各种模型超参数,例如学习速率和特征。所以在新数据基础上将数据集划分为三个子集,可以大幅降低过拟合的发生几率:划分训练集、验证集和测试集
- 在模型“通过”验证集之后,使用测试集再次检查评估结果。
train_num = 300 # 训练集的数目
valid_num = 100 # 验证集的数目
test_num = len(x_data) - train_num - valid_num # 测试集的数日 = 506-训练集的数日–验证集的数月
# 训练集划分
x_train = x_data[:train_num]
y_train = y_data[:train_num]
# 验证集划分
x_valid = x_data[train_num:train_num+valid_num]
y_valid = y_data[train_num:train_num+valid_num]
# 测试集划分
x_test = x_data[train_num+valid_num:train_num+valid_num+test_num]
y_test = y_data[train_num+valid_num:train_num+valid_num+test_num]
- 数据类型的转换
# 转换为tf.float32数据类型,后面求损失时要和变量W执行tf.matmul操作
x_train = tf.cast(x_train,dtype=tf.float32)
x_valid = tf.cast(x_valid,dtype=tf.float32)
x_test = tf.cast(x_test,dtype=tf.float32)
- 构建模型
def model(x,w,b):
return tf.matmul(x,w)+b
- 优化变量的创建
W = tf.Variable(tf.random.normal([12,1],mean=0.0,stddev=1.0,dtype=tf.float32))
B= tf.Variable(tf.zeros(1),dtype = tf.float32)
print(W)
print(B)
输出为: 文章来源:https://www.toymoban.com/news/detail-423597.html
文章来源:https://www.toymoban.com/news/detail-423597.html
- 模型训练
# 设置超参数
training_epochs = 50 #迭代次数
learning_rate = 0.001 #学习率
batch_size = 10 #批量训练一次的样本数
# 定义损失函数
# 采用均方差作为损失函数
def loss(x,y,w,b):
err = model(x, w,b) - y # 计算模型预测值和标签值的差异
squared_err = tf.square(err) # 求平方,得出方差
return tf.reduce_mean(squared_err) # 求均值,得出均方差.
# 定义梯度函数
#计算样本数据[x,y]在参数[w, b]点上的梯度
def grad(x,y,w,b):
with tf.GradientTape() as tape:
loss_= loss(x,y,w,b)
return tape.gradient(loss_,[w,b]) #返回梯度向量
# 选择优化器
optimizer = tf.keras.optimizers.SGD(learning_rate) #创建优化器,指定学习率
# 迭代训练
loss_list_train = [] # 用于保存训练集1oss值的列表
loss_list_valid = [] # 用于保存验证集loss值的列表
total_step = int(train_num/batch_size)# 转换为整型
for epoch in range(training_epochs):
for step in range(total_step):
xs = x_train[step*batch_size:(step+1)*batch_size,:]
ys = y_train[step*batch_size:(step+1)*batch_size]
grads = grad(xs,ys,W,B) # 计算梯度
optimizer.apply_gradients(zip(grads,[W,B]))# 优化器根据梯度自动调整变量w和b
loss_train = loss(x_train,y_train,W,B).numpy() # 计算当前轮训练损失
loss_valid = loss(x_valid,y_valid,W,B).numpy() # 计算当前轮验证损失
loss_list_train.append(loss_train)
loss_list_valid.append(loss_valid)
print("epoch={:3d},train_loss={:.4f},valid_loss={:.4f}".format(epoch+1,loss_train,loss_valid))
输出为:迭代50次,但是由于训练集和验证集损失都为nan就没有继续下去了。
可以参考一下:https://itcn.blog/p/1026265732.html文章来源地址https://www.toymoban.com/news/detail-423597.html
epoch= 1,train_loss=nan,valid_loss=nan
epoch= 2,train_loss=nan,valid_loss=nan
epoch= 3,train_loss=nan,valid_loss=nan
epoch= 4,train_loss=nan,valid_loss=nan
epoch= 5,train_loss=nan,valid_loss=nan
epoch= 6,train_loss=nan,valid_loss=nan
epoch= 7,train_loss=nan,valid_loss=nan
epoch= 8,train_loss=nan,valid_loss=nan
epoch= 9,train_loss=nan,valid_loss=nan
epoch= 10,train_loss=nan,valid_loss=nan
epoch= 11,train_loss=nan,valid_loss=nan
epoch= 12,train_loss=nan,valid_loss=nan
epoch= 13,train_loss=nan,valid_loss=nan
epoch= 14,train_loss=nan,valid_loss=nan
epoch= 15,train_loss=nan,valid_loss=nan
epoch= 16,train_loss=nan,valid_loss=nan
epoch= 17,train_loss=nan,valid_loss=nan
epoch= 18,train_loss=nan,valid_loss=nan
epoch= 19,train_loss=nan,valid_loss=nan
epoch= 20,train_loss=nan,valid_loss=nan
epoch= 21,train_loss=nan,valid_loss=nan
epoch= 22,train_loss=nan,valid_loss=nan
epoch= 23,train_loss=nan,valid_loss=nan
epoch= 24,train_loss=nan,valid_loss=nan
epoch= 25,train_loss=nan,valid_loss=nan
epoch= 26,train_loss=nan,valid_loss=nan
epoch= 27,train_loss=nan,valid_loss=nan
epoch= 28,train_loss=nan,valid_loss=nan
epoch= 29,train_loss=nan,valid_loss=nan
epoch= 30,train_loss=nan,valid_loss=nan
epoch= 31,train_loss=nan,valid_loss=nan
epoch= 32,train_loss=nan,valid_loss=nan
epoch= 33,train_loss=nan,valid_loss=nan
epoch= 34,train_loss=nan,valid_loss=nan
epoch= 35,train_loss=nan,valid_loss=nan
epoch= 36,train_loss=nan,valid_loss=nan
epoch= 37,train_loss=nan,valid_loss=nan
epoch= 38,train_loss=nan,valid_loss=nan
epoch= 39,train_loss=nan,valid_loss=nan
epoch= 40,train_loss=nan,valid_loss=nan
epoch= 41,train_loss=nan,valid_loss=nan
epoch= 42,train_loss=nan,valid_loss=nan
epoch= 43,train_loss=nan,valid_loss=nan
epoch= 44,train_loss=nan,valid_loss=nan
epoch= 45,train_loss=nan,valid_loss=nan
epoch= 46,train_loss=nan,valid_loss=nan
epoch= 47,train_loss=nan,valid_loss=nan
epoch= 48,train_loss=nan,valid_loss=nan
epoch= 49,train_loss=nan,valid_loss=nan
epoch= 50,train_loss=nan,valid_loss=nan
到了这里,关于机器学习10—多元线性回归模型的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!