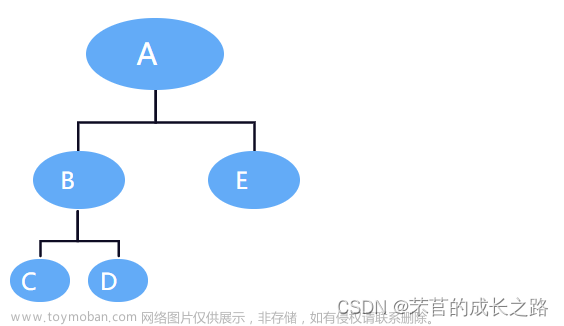
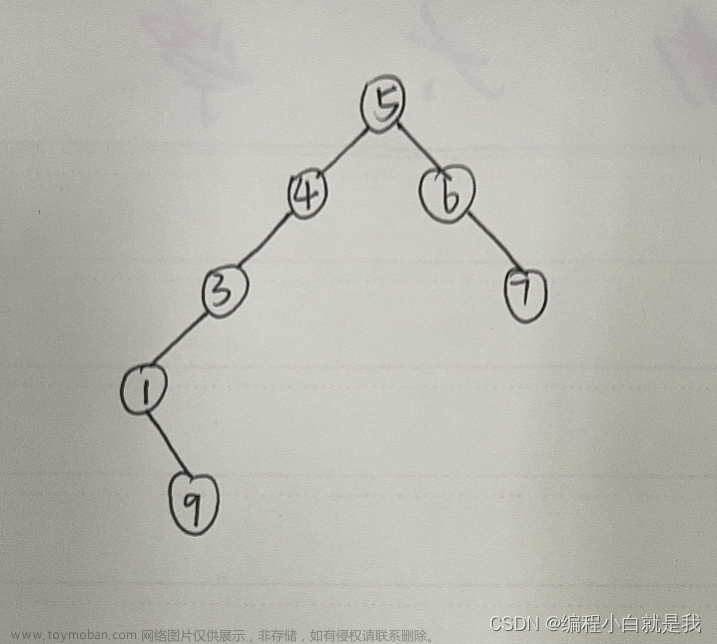
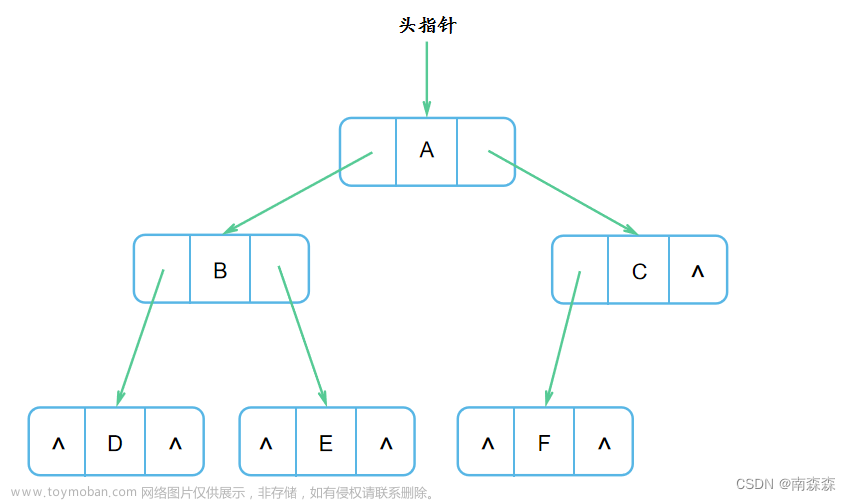
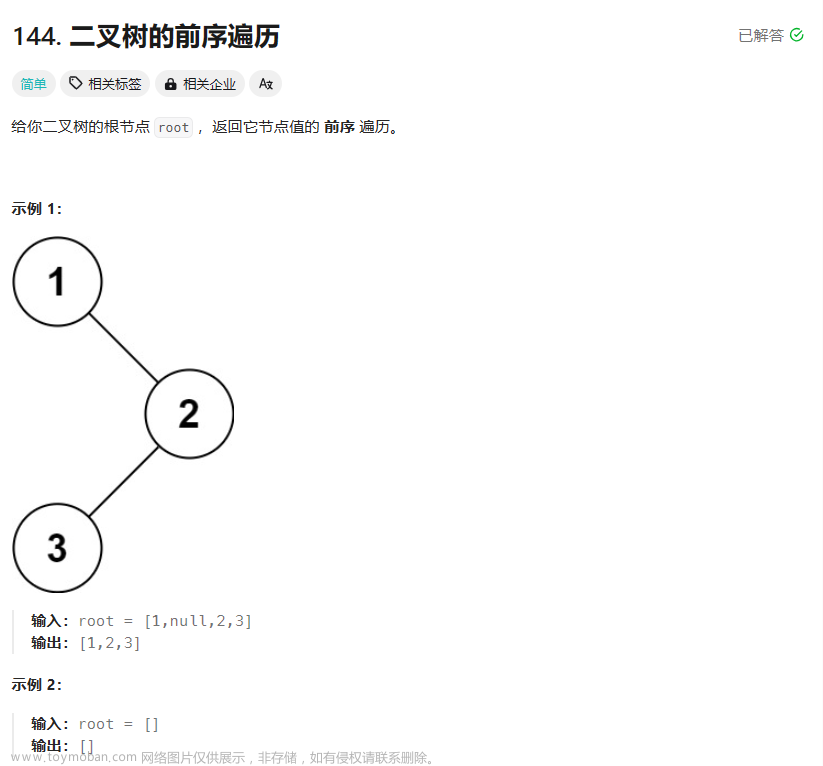
{用先序讲解举例,请自己联系中序和后序(在最后):}
(在自己作为儿子的同时自己也是根)
注意:递归的形参不是你看到的形参,而是逻辑上的形参!
首先是创建的函数,如果我们要先序输入这样一个二叉树:那么我们在计算机内部其实是要先序输入:ab##c##的,【这里的‘#’用来表示没有数值了,把传入的形参置空NULL】

所以create创造函数里面的if-else语句第一次走else建立根结点,然后进入T->lchild
( p->lchild=create(p->lchild,name,index); ),递归这个函数,左儿子判断为b,所以进入else,又递归( p->lchild=create(p->lchild,name,index); )语句,判断为‘#’,进入if,说明这次的结点应该是空的,return NULL; 回到递归上一级的地方执行( p->rchild=create(p->rchild,name,index); ),这个函数的递归上一级是b的rchild,所以把b->rchild置空,回到再再上一级,也就是a的那一层,进入a->rchild...
以上是创建,遍历的时候,因为之前的函数是把地址置空,所以,在遍历函数中if的判断也是对当前形参的地址进行操作的。

/*二叉树的实现【创建与遍历】*/
#include<stdio.h>
#include<stdlib.h>
typedef struct Bigtree{
char data;
struct Bigtree *lchild;
struct Bigtree *rchild;
}Bigtree;
Bigtree* create(Bigtree *T,char name[],int *index);
void preoder(Bigtree *T);
int main(){
Bigtree *T;
char name[50]={"ab##c##"};
int index=0;
T=create(T,name,&index);
printf("\n先序遍历为:");
preoder(T);
return 0;
}
//创建[先序创建]
Bigtree* create(Bigtree *T,char name[],int *index) //不改变n的值,所以不是int* n
{
char ch;
ch=name[*index];
//(*index)++;
Bigtree *p=T;
if(name[(*index)]=='#'){
*index+=1;
p=NULL; //T是形参,每一次传的参数不一样!
return p; //记得‘#’要返回空
}else{
p=(Bigtree*)malloc(sizeof(Bigtree));
p->data=ch;
*index+=1;
p->lchild=create(p->lchild,name,index);
p->rchild=create(p->rchild,name,index);
}
return p;
}
//先序遍历
int i=0;
void preoder(Bigtree *T)
{
//printf("\norderT,[%d]==%p",++i,T);
if(T==NULL){
return;
}else{
printf("%c ",T->data);
preoder(T->lchild);
preoder(T->rchild);
}
}
-------------------------------分割线------------------------文章来源:https://www.toymoban.com/news/detail-423651.html
中序与后序遍历的代码:文章来源地址https://www.toymoban.com/news/detail-423651.html
//中序遍历
void inoder(Bigtree *T)
{
if(T==NULL){
return;
}else{
preoder(T->lchild);
printf("%c ",T->data);
preoder(T->rchild);
}
} //后序遍历
void underoder(Bigtree *T)
{
if(T==NULL){
return;
}else{
preoder(T->lchild);
preoder(T->rchild);
printf("%c ",T->data);
}
}
到了这里,关于二叉树的创建与遍历的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!