参数与非参数检验：理解差异并正确使用-Toy模板网

这篇具有很好参考价值的文章主要介绍了参数与非参数检验：理解差异并正确使用。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

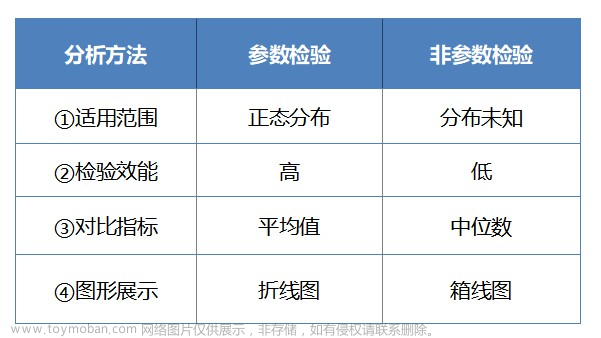
数据科学是一个快速发展的领域，它在很大程度上依赖于统计技术来分析和理解复杂的数据集。这个过程的一个关键部分是假设检验，它有助于确定从样本中获得的结果是否可以推广到总体。

在这篇文章中，我们将探讨参数与非参数检验之间的区别，提供示例以更好地理解它们的用例，并总结关键要点。

理解假设检验

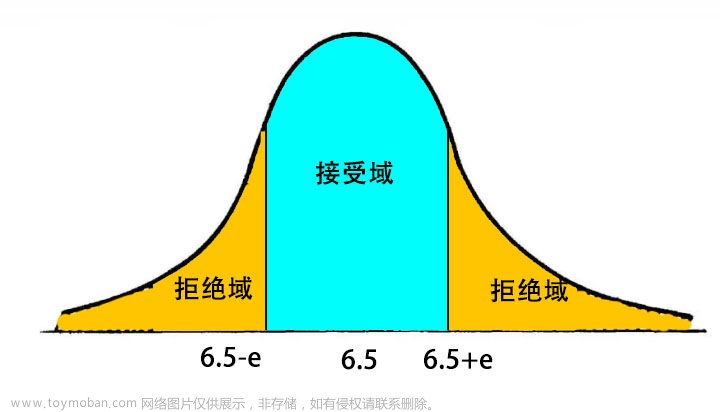
假设检验是一种统计方法，用于确定给定结果是由于偶然或特定影响的可能性。它包括制定一个零假设(H0)和一个备选假设(H1)，然后使用统计检验来确定哪一个更有可能。

检验的选择取决于数据的特征、变量的分布和检验的假设。这就是参数和非参数测试发挥作用的地方。

参数与非参数检验：理解差异并正确使用

参数检验

参数检验是对数据的基本分布做出某些假设的统计测试。这些检验假定数据呈正态分布、方差相等且样本独立。参数检验通常基于总体参数的假设，例如总体均值、方差等已知或假设的数值，通过样本数据对总体参数进行推断和判断一些常见的参数测试包括：

1、T检验

t 检验用于比较两组的均值。它可以用来判断两个样本的均值是否存在显着差异，例如两个不同班级的平均考试成绩。

2、方差分析(ANOVA)

方差分析用于比较三个或更多组的均值。该检验有助于确定多个群体的的均值之间是否存在任何显着差异，例如比较不同营销策略的性能。

3、皮尔森的相关性

皮尔逊相关是用来衡量两个连续变量之间的线性关系的强度和方向。例如，它可以用来确定学习的小时数和最终的考试成绩之间是否存在关系。

非参数检验

非参数检验是不对数据的基本分布做出任何假设的统计检验。非参数检验则不需要对总体参数进行假设或推断，而是通过对数据的排序、计数等简单操作来进行假设检验。非参数检验方法通常比参数检验方法更加灵活，但也相对更加保守和低效。一些常见的非参数检验包括：

1、Mann-Whitney U检验

Mann-Whitney U 检验也称为Wilcoxon秩和检验。它用于比较两个独立的样本，判断它们是否来自于同一个总体分布。例如，它可用于比较两个社区的收入中位数。

2、Kruskal-Wallis H 检验

Kruskal-Wallis H 检验用于比较三个或以上独立样本的中位数是否相同，也称为方差分析的非参数替代方法。当数据不满足参数检验所需的假设时，它可以替代方差分析，用来比较使用不同产品的客户的满意度。

3、Spearman相关性

Spearman’s Rank Correlation用于度量两个变量之间的相关性。它通过将两个变量的值转换为排名，然后计算这些排名之间的相关性，从而可以处理非线性关系和离群值的影响。例如，它可用于确定运动员在比赛中的排名与其经验年数之间是否存在关系。

如何选择参数和非参数检验

在参数测试和非参数检验之间进行选择取决于几个因素，例如:

数据分布：如果数据呈正态分布，则参数检验更合适，因为它们具有更强的统计能力（更擅长检测显着影响）。如果数据不是正态分布的，则应使用非参数检验，因为它们对数据的假设较少。
样本大小：当样本大小较小时，非参数检验更适合，因为它们对样本分布的假设更少。当样本大小较大时，参数检验更可靠。这是因为非参数检验对违反假设的敏感性较低，而这种情况更可能发生在小样本中。
等方差：参数检验假定各组之间的方差相等。如果数据不是等方差的，则应改用非参数测试。
数据分布的偏斜程度：如果数据分布严重偏斜，则非参数检验可能更可靠，因为它们对分布的假设更少。
检验目的：如果需要检验的是中位数、百分位数、比例等非参数统计量，那么非参数检验更适合。如果需要检验均值、标准差等参数统计量，那么参数检验更可靠。

总结

假设检验是数据科学的基本组成部分，有助于确定从样本中获得的结果是否可以推广到总体。参数检验对数据的基本分布做出假设，例如正态分布、等方差和独立样本。非参数检验更灵活，可以在数据不满足参数检验所需的假设时使用。在参数检验和非参数检验之间进行选择取决于数据的特征、样本大小和检验所做的假设。本文介绍的参数检验的示例包括 t 检验、方差分析和 Pearson 相关性，而非参数检验包括 Mann-Whitney U 检验、Kruskal-Wallis H 检验和 Spearman 等级相关性。

通过了解参数和非参数测试之间的差异以及何时使用每种类型，我们可以在数据分析中做出更明智的决策，最终获得更准确和可靠的结果。

https://avoid.overfit.cn/post/f516ef963cd54d61bc7d702337c69f48

作者：Andrew Austin文章来源地址https://www.toymoban.com/news/detail-423666.html

到了这里，关于参数与非参数检验：理解差异并正确使用的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！