特征方程和通项公式
如果数列 a n a_n an的递推公式: a n = c 1 a n − 1 + c 2 a n − 2 a_n=c_1a_{n-1}+c_2a_{n-2} an=c1an−1+c2an−2------(1)
根据待定系数法,假设
a
n
−
x
a
n
−
1
=
y
(
a
n
−
1
−
x
a
n
−
2
)
a_n-xa_{n-1}=y(a_{n-1}-xa_{n-2})
an−xan−1=y(an−1−xan−2)-----(2)
(1)和(2)比较得

根据韦达定理, x , y x,y x,y是方程 t 2 − c 1 t − c 2 = 0 t^2-c_1t-c_2=0 t2−c1t−c2=0的两个根,我们也将这个方程称为数列 a n a_n an的特征方程
根据方程(2)可以推出 a n − x a n − 1 = y n − 1 ( a 1 − x a 0 ) a_n-xa_{n-1}=y^{n-1}(a_1-xa_0) an−xan−1=yn−1(a1−xa0)(等比数列)-----(3)
下面我们将两个根
t
1
,
t
2
t_1,t_2
t1,t2分别带入方程(3)得
将 ( 5 ) ∗ t 1 − ( 4 ) ∗ t 2 (5)*t_1-(4)*t_2 (5)∗t1−(4)∗t2得
( t 1 − t 2 ) a n = ( a 1 − t 2 a 0 ) t 1 n − ( a 1 − t 1 a 0 ) t 2 n (t_1-t_2)a_n=(a_1-t_2a_0)t_1^n-(a_1-t_1a_0)t_2^n (t1−t2)an=(a1−t2a0)t1n−(a1−t1a0)t2n
再整理得
a n = a 1 − t 2 a 0 t 1 − t 2 t 1 n − a 1 − t 1 a 0 t 1 − t 2 t 2 n a_n=\frac{a_1-t_2a_0}{t_1-t_2}t_1^n-\frac{a_1-t_1a_0}{t_1-t_2}t_2^n an=t1−t2a1−t2a0t1n−t1−t2a1−t1a0t2n
而 a 0 , a 1 , t 1 , t 2 a_0,a_1,t_1,t_2 a0,a1,t1,t2均已知,可当作常项,于是 a n a_n an的通项公式:
a
n
=
A
t
1
n
+
B
t
2
n
a_n=At_1^n+Bt_2^n
an=At1n+Bt2n
t
1
,
t
2
t_1,t_2
t1,t2是特征方程的两个根
A
,
B
A,B
A,B为常项,一般通过待定系数法求出
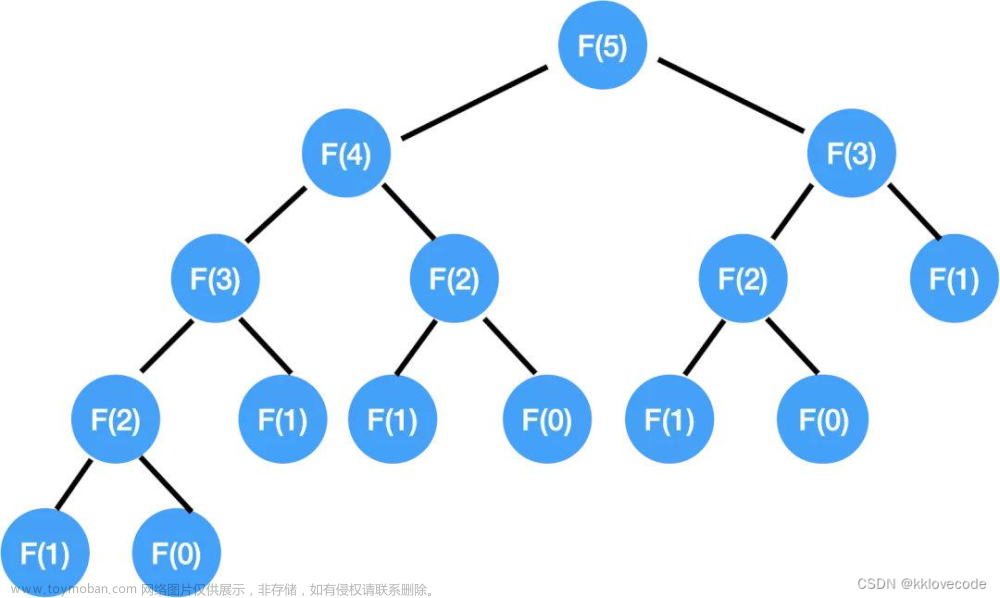
斐波那契通项公式
斐波那契数列的递推公式: a n = a n − 1 + a n − 2 a_n=a_{n-1}+a_{n-2} an=an−1+an−2
于是特征方程为: x 2 − x − 1 = 0 x^2-x-1=0 x2−x−1=0的两个根: x 1 = 1 + 5 2 x_1=\frac{1+\sqrt5}{2} x1=21+5和 x 2 = 1 − 5 2 x_2=\frac{1-\sqrt5}{2} x2=21−5
则 a n = A x 1 n + B x 2 n a_n=Ax_1^n+Bx_2^n an=Ax1n+Bx2n,将 a 1 = 1 , a 2 = 1 a_1=1,a_2=1 a1=1,a2=1带入可求得 A = 1 5 , B = − 1 5 A=\frac{1}{\sqrt5},B=-\frac{1}{\sqrt5} A=51,B=−51文章来源:https://www.toymoban.com/news/detail-423867.html
即通项公式: a n = 1 5 [ ( 1 + 5 2 ) n − ( 1 − 5 2 ) n ] a_n=\frac{1}{\sqrt5}[(\frac{1+\sqrt5}{2})^n-(\frac{1-\sqrt5}{2})^n] an=51[(21+5)n−(21−5)n]文章来源地址https://www.toymoban.com/news/detail-423867.html
到了这里,关于【算法】斐波那契数列通项公式的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!