目录
1.动态规划算法
2.跳跃游戏(一)
1.题目
2.初步分析
3.代码实现
3.跳跃游戏(二)
1.题目
2.初步分析
3.代码实现
1.动态规划算法
动态规划(英语:Dynamic programming,简称 DP),是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的,通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。动态规划常常适用于有重叠子问题和最优子结构性质的问题。
简单来说,动态规划就是把给定的问题拆分成一个个子问题,直到子问题可以直接解决,和递归不同的是,动态规划可以将子问题的答案储存起来,减少重复计算,大大减少了时间复杂度。
下面我们通过两个简单的例题来步入动态规划的大门!
2.跳跃游戏(一)
1.题目
描述
给定一个非负整数数组nums,假定最开始处于下标为0的位置,数组里面的每个元素代表下一跳能够跳跃的最大长度。如果能够跳到数组最后一个位置,则输出true,否则输出false。
输入描述:
第一行输入一个正整数 n ,表示数组 nums 的长度
第二行输入 n 个整数表示数组的每个元素
输出描述:
输出 true 或者 false
2.初步分析
首先,我们可以发现,本道题具有重叠子问题的特点。要求是否能跳到第n格,可以先将其拆分成能否跳到第n-1格,第n-2格...第1格多个子问题,通过求出一步步求出子问题的答案,如果子问题都成立,原问题是否成立就迎刃而解了。
我的思路是:创建一个变量k存储能跳跃的最大距离,自下而上遍历整个数组,不断的更新k的值,当遍历num[i]的过程中,如果i始终小于等于k,即所有子问题都成立,如果出现i>k的情况,则子问题不成立,原问题也就输出false,主要代码如下:
3.代码实现
#include<stdio.h>
#include<stdlib.h>
int main() {
int n = 0;
int i = 0;
scanf("%d", &n);
//动态开辟num数组
int* num = (int*)malloc(n * sizeof(int));
for (int i = 0; i < n; i++)
{
scanf("%d", &num[i]);
}
int k = 0; //表示能走的最大距离
for (i = 0; i < n; i++) //自下而上遍历
{
if (i > k) //即走不到第i格,子问题不成立
{
printf("false");
break;
}
k = k > (i + num[i]) ? k:(i+num[i]); //更新k的值
}
if (i == n) //子问题都成立,且可以走到最后一个
{
printf("true");
}
free(num);
return 0;
}3.跳跃游戏(二)
1.题目
描述
给定一个非负整数数组nums,假定最开始处于下标为0的位置,数组里面的每个元素代表下一跳能够跳跃的最大长度,如果可以跳到数组最后一个位置,请你求出跳跃路径中所能获得的最多的积分。
1.如果能够跳到数组最后一个位置,才能计算所获得的积分,否则积分值为-1
2.如果无法跳跃(即数组长度为0),也请返回-1
3.数据保证返回的结果不会超过整形范围,即不会超过2^{31}-1231−1
输入描述:
第一行输入一个正整数 n 表示数组 nums的长度
第二行输入 n 个整数,表示数组 nums 的所有元素的值
输出描述:
输出能获得的最多的积分
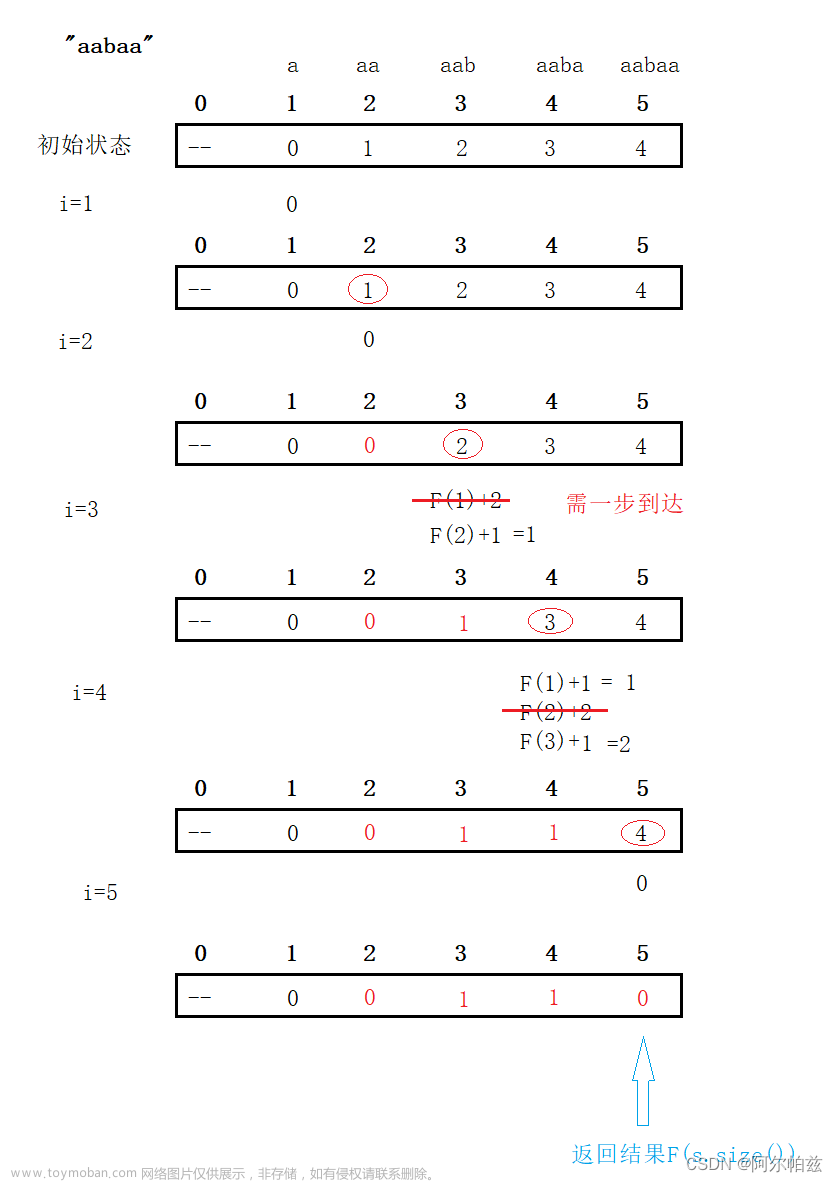
2.初步分析
这题在上一道题的基础上增加了求最高积分的条件,因此,不仅拥有重叠子问题的特点,还有最优子结构的特点。我们可以发现跳到第i格的最高积分一定是可以跳到第i格的最近格子跳上来的。因此我们可以在上一题的遍历中进行扩展,增加一个循环来求出到这个子问题的最多积分。
我的思路是:在自下而上的遍历整个数组时,增加一个循环,自上而下遍历,如果遇到num[j]+j>=i,就代表这是可以跳到i的最近格子(其中i代表第i个格子,j代表0-i中的中的一个格子)。而利用动态规划的思想,我们可以创建一个一维数组dp,存储跳到每一格的最大积分,最终一步步求出跳到第n格的最大积分。主要代码如下:
3.代码实现
#include <stdio.h>
#include<stdlib.h>
int max(int x, int y) //返回可达到最大距离函数
{
return x > y ? x : y;
}
int main()
{
int n = 0; //代表格数
int i = 0; //用于循环遍历
int k = 0; //表示最大跳跃距离
scanf("%d", &n);
int* num = (int*)malloc(n * sizeof(int));
int* dp = (int*)malloc(n * sizeof(int)); //存储每个子问题即跳到第i格的最大积分
for (i = 0; i < n; i++)
{
scanf("%d", &num[i]);
}
dp[0] = num[0]; //赋初值,跳到第1格的最大积分即为自身
if (n == 0) //空数组
{
printf("-1\n");
return 0;
}
if (n == 1) //只有一个格子,最大积分即为自身
{
printf("%d\n", dp[0]);
return 0;
}
for (i = 0; i < n; i++) //自下而上遍历,寻找最大距离
{
if (i <= k) //子问题成立
{
int j = 0;
k = max(k, i + num[i]); //更新最大距离
for (j = i - 1; j >= 0; j--) //自上而下,求出子问题的最大积分
{
if (j + num[j] >= i) //找到可跳到i最近的格子j
{
dp[i] = dp[j] + num[i]; //第i格的最大积分即为j的最大积分加上num[i]
break;
}
}
}
else //子问题不成立,无法跳到第i格
{
printf("-1\n");
return 0;
}
}
printf("%d", dp[n - 1]); //所有子问题均成立,则到终点最大积分就为dp的最后
//一个元素
free(num);
free(dp);
return 0;
}以上,就是动态规划入门刷题(一)的全部内容。文章来源:https://www.toymoban.com/news/detail-424141.html
制作不易,能否点个赞再走呢qwq文章来源地址https://www.toymoban.com/news/detail-424141.html
到了这里,关于C语言刷题之动态规划入门(一)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!