[HDU - 4578]Transformation（线段树+多重懒标记）-Toy模板网

这篇具有很好参考价值的文章主要介绍了[HDU - 4578]Transformation（线段树+多重懒标记）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

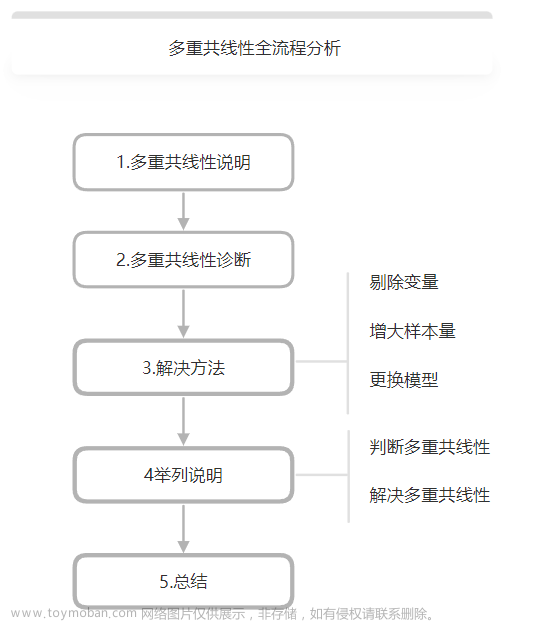
一、问题

[HDU - 4578]Transformation（线段树+多重懒标记）

二、分析

这道题涉及到了区间操作，所以我们用线段树算法。同时，这道题里面有区间修改的操作，所以我们还要用到懒标记。

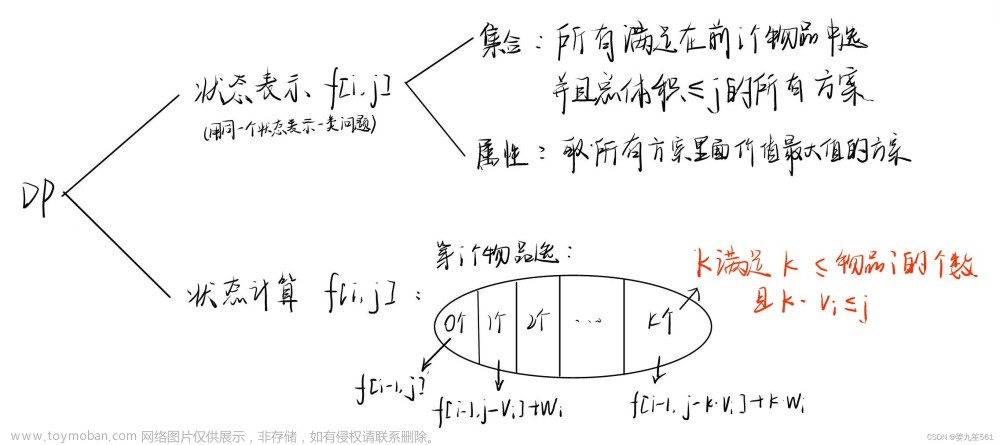
这里一共有三种区间的操作，分别是：加、乘、赋值。这三种操作无法用一个懒标记来统一，所以我们需要使用三个懒标记来完成这道题。

这道题的查询操作也分为三种，一次方的和、二次方的和、三次方的和。

所以我们需要去维护三种 $s u m$ 。

1、节点定义

/*
tag_1 --> 加法
tag_2 --> 乘法
tag_3 --> 赋值
*/
struct Node
{
	int l, r;
	int sum1, sum2, sum3;
	int tag_1, tag_2, tag_3;
}tre[N * 4];

2、pushup

$p u s h u p$ 函数就是利用子节点来更新父节点，这个操作比较简单，直接合并三种和即可。

//lson 是左儿子， rson是右儿子
void pushup(int u)
{
	tre[u].sum1 = (tre[lson].sum1 + tre[rson].sum1) % mod;
	tre[u].sum2 = (tre[lson].sum2 + tre[rson].sum2) % mod;
	tre[u].sum3 = (tre[lson].sum3 + tre[rson].sum3) % mod;
}

3、pushdown

$p u s h d o w n$ 操作是将三种懒标记下传的操作。这里需要注意两个问题：
1、每种标记如何下传？
2、三种标记之间下传的优先级问题。

（1）每种标记如何下传？

赋值

赋值公式如下图所示：
[HDU - 4578]Transformation（线段树+多重懒标记）
$l e n = r - l + 1$
另外需要注意在计算过程中进行取模。

乘法

如下图所示：
[HDU - 4578]Transformation（线段树+多重懒标记）
提取公因式即可。

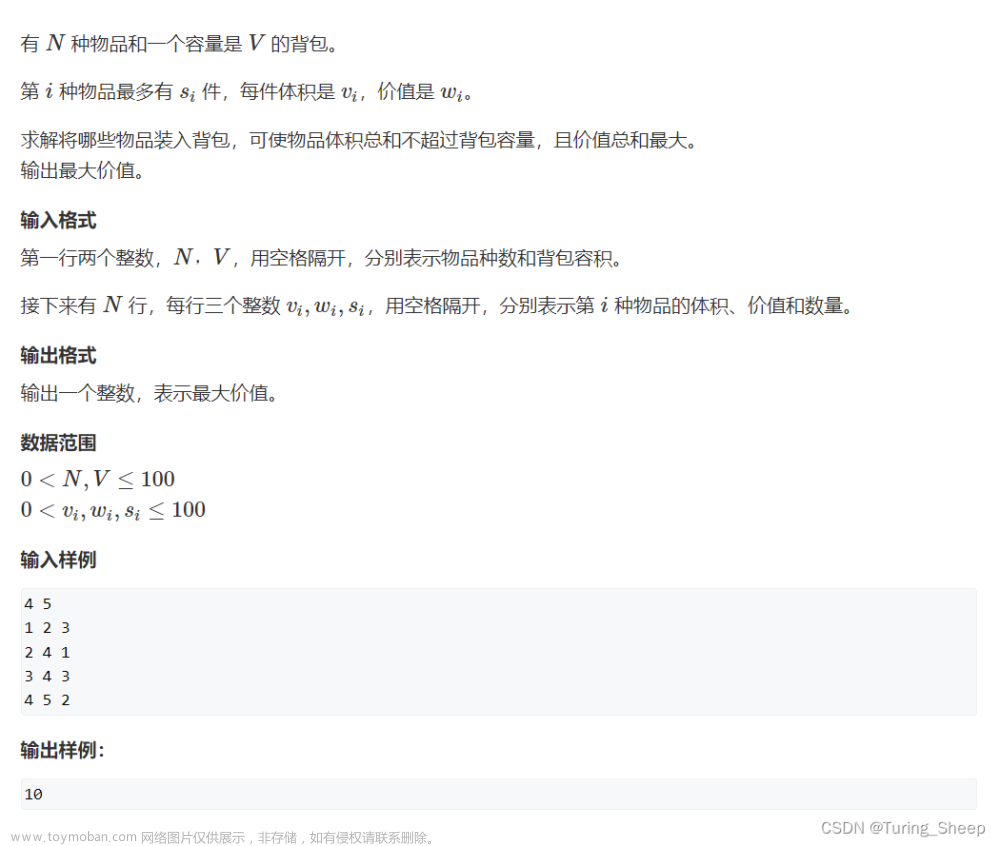
加法

加法是最难处理的，分类讨论一下。
先说一次方。
[HDU - 4578]Transformation（线段树+多重懒标记）
再说二次方

最后说三次方

（2）三种标记下传的优先级问题

对于某一个区间而言，三种操作可能同时出现。当出现赋值操作的时候，说明在此操作之前出现的加、乘都没有用了，因为都被当前的赋值操作覆盖掉了。所以我们最先考虑的是赋值操作。

如果该区间没有赋值操作，我们考虑的就是乘法操作，乘法出现的时候，说明在此次操作之前的加法操作的数值p也同样需要翻对应的倍数。

最后我们考虑加法。

综合上述讨论，我们可以写出下面的函数实现：

另外我们需要注意，在下传的过程中，我们要将左右区间的标记转化到对应的数值上。

void pushdown(int u)
{
	auto &root = tre[u], &left = tre[lson], &right = tre[rson];
	if(root.tag_3)
	{
		int c = root.tag_3;
		int len1 = (left.r - left.l + 1);
		left.sum1 = len1 * c % mod;
		left.sum2 = len1 * c * c % mod;
		left.sum3 = len1 * c % mod * c % mod * c % mod;
		
		int len2 = (right.r - right.l + 1);
		right.sum1 = len2 * c % mod;
		right.sum2 = len2 * c * c % mod;
		right.sum3 = len2 * c * c * c % mod;
		
		left.tag_3 = right.tag_3 = c;
		left.tag_1 = right.tag_1 = 0;
		left.tag_2 = right.tag_2 = 1;
		root.tag_3 = 0;
	}
	if(root.tag_2 != 1)
	{
		int c = root.tag_2;
		left.sum1 = left.sum1 * c % mod;
		left.sum2 = left.sum2 * c * c % mod;
		left.sum3 = left.sum3 * c * c * c % mod;

		right.sum1 = right.sum1 * c % mod;
		right.sum2 = right.sum2 * c * c % mod;
		right.sum3 = right.sum3 * c * c * c % mod;		
		
		right.tag_2 = c * right.tag_2 % mod;
		left.tag_2 = c * left.tag_2 % mod;

		right.tag_1 = c * right.tag_1 % mod;
		left.tag_1 = c * left.tag_1 % mod;

		root.tag_2 = 1; 
	}

	if(root.tag_1)
	{
		int c = root.tag_1;

		int s1 = left.sum1;
		int s2 = left.sum2;
		
		int len1 = left.r - left.l + 1;
		left.sum1 = (left.sum1 + len1 * c) % mod;
		left.sum2 = (left.sum2 + 2 * s1 * c + len1 * c * c) % mod;
		left.sum3 = (left.sum3 + 3 * c * s2 + 3 * s1 * c * c + len1 * c * c * c) % mod;
		
		s1 = right.sum1;
		s2 = right.sum2;
		int len2 = right.r - right.l + 1;
		right.sum1 = (right.sum1 + len2 * c) % mod;
		right.sum2 = (right.sum2 + 2 * s1 * c + len2 * c * c % mod) % mod;
		right.sum3 = (right.sum3 + 3 * c * s2 % mod + 3 * s1 * c * c % mod + len2 * c % mod * c % mod * c % mod ) % mod;
		
		left.tag_1 = (c + left.tag_1) % mod;
		right.tag_1 = (c + right.tag_1) % mod;
		root.tag_1 = 0;
	}
}

以上就是这道题所有的难点，剩下的函数操作就比较常规了。大家直接看代码实现即可。文章来源地址https://www.toymoban.com/news/detail-424327.html

三、代码

#include<bits/stdc++.h>
#define endl '\n'
#define INF 0x3f3f3f3f
#define lson u << 1
#define rson u << 1 | 1
#define int long long
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int N = 1e5 + 10;
const int mod = 1e4 + 7;
int n, m;
struct Node
{
	int l, r;
	int sum1, sum2, sum3;
	int tag_1, tag_2, tag_3;
}tre[N * 4];

void pushup(int u)
{
	tre[u].sum1 = (tre[lson].sum1 + tre[rson].sum1) % mod;
	tre[u].sum2 = (tre[lson].sum2 + tre[rson].sum2) % mod;
	tre[u].sum3 = (tre[lson].sum3 + tre[rson].sum3) % mod;
}

void pushdown(int u)
{
	auto &root = tre[u], &left = tre[lson], &right = tre[rson];
	if(root.tag_3)
	{
		int c = root.tag_3;
		int len1 = (left.r - left.l + 1);
		left.sum1 = len1 * c % mod;
		left.sum2 = len1 * c * c % mod;
		left.sum3 = len1 * c % mod * c % mod * c % mod;
		
		int len2 = (right.r - right.l + 1);
		right.sum1 = len2 * c % mod;
		right.sum2 = len2 * c * c % mod;
		right.sum3 = len2 * c * c * c % mod;
		
		left.tag_3 = right.tag_3 = c;
		left.tag_1 = right.tag_1 = 0;
		left.tag_2 = right.tag_2 = 1;
		root.tag_3 = 0;
	}
	if(root.tag_2 != 1)
	{
		int c = root.tag_2;
		left.sum1 = left.sum1 * c % mod;
		left.sum2 = left.sum2 * c * c % mod;
		left.sum3 = left.sum3 * c * c * c % mod;

		right.sum1 = right.sum1 * c % mod;
		right.sum2 = right.sum2 * c * c % mod;
		right.sum3 = right.sum3 * c * c * c % mod;		
		
		right.tag_2 = c * right.tag_2 % mod;
		left.tag_2 = c * left.tag_2 % mod;

		right.tag_1 = c * right.tag_1 % mod;
		left.tag_1 = c * left.tag_1 % mod;

		root.tag_2 = 1; 
	}

	if(root.tag_1)
	{
		int c = root.tag_1;

		int s1 = left.sum1;
		int s2 = left.sum2;
		
		int len1 = left.r - left.l + 1;
		left.sum1 = (left.sum1 + len1 * c) % mod;
		left.sum2 = (left.sum2 + 2 * s1 * c + len1 * c * c) % mod;
		left.sum3 = (left.sum3 + 3 * c * s2 + 3 * s1 * c * c + len1 * c * c * c) % mod;
		
		s1 = right.sum1;
		s2 = right.sum2;
		int len2 = right.r - right.l + 1;
		right.sum1 = (right.sum1 + len2 * c) % mod;
		right.sum2 = (right.sum2 + 2 * s1 * c + len2 * c * c % mod) % mod;
		right.sum3 = (right.sum3 + 3 * c * s2 % mod + 3 * s1 * c * c % mod + len2 * c % mod * c % mod * c % mod ) % mod;
		
		left.tag_1 = (c + left.tag_1) % mod;
		right.tag_1 = (c + right.tag_1) % mod;
		root.tag_1 = 0;
	}
}

void build(int u, int l, int r)
{
	if(l == r)
	{
		tre[u] = {l, r};
		tre[u].tag_2 = 1;
		return;
	}
	int mid = l + r >> 1;
	tre[u] = {l, r};
	tre[u].tag_2 = 1;
	build(lson, l, mid);
	build(rson, mid + 1, r);
}

void modify(int u, int l, int r, int c, int op)
{
	if(tre[u].l >= l && tre[u].r <= r)
	{
		auto &root = tre[u];
		if(op == 1)
		{
			int s1 = root.sum1;
			int s2 = root.sum2;
			root.sum1 = (root.sum1 + (root.r - root.l + 1) * c) % mod;
			root.sum2 = (root.sum2 + 2 * s1 * c % mod + (root.r - root.l + 1) * c % mod * c % mod) % mod;
			root.sum3 = (root.sum3 + 3 * c * s2 % mod + 3 * s1 * c * c % mod + (root.r - root.l + 1) * c % mod * c * c % mod ) % mod;
			root.tag_1 = (c + root.tag_1) % mod;
		}
		else if(op == 2)
		{
			root.sum1 = root.sum1 * c % mod;	
			root.sum2 = root.sum2 * c * c % mod;
			root.sum3 = root.sum3 * c % mod * c % mod * c % mod;
			root.tag_2 = c * root.tag_2 % mod;
			root.tag_1 = c * root.tag_1 % mod;
		}
		else
		{
			root.sum1 = (root.r - root.l + 1) * c % mod;
			root.sum2 = (root.r - root.l + 1) * c * c % mod;
			root.sum3 = (root.r - root.l + 1) * c % mod * c % mod * c % mod;
			root.tag_3 = c;
			root.tag_1 = 0;
			root.tag_2 = 1;
		}
		return;
	}
	pushdown(u);
	int mid = tre[u].l + tre[u].r >> 1;
	if(l <= mid)
		modify(lson, l, r, c, op);

	if(r > mid)
		modify(rson, l, r, c, op);

	pushup(u);
}

int query(int u, int l, int r, int op)
{
	if(tre[u].l >= l && tre[u].r <= r)
	{
		if(op == 1)
			return tre[u].sum1;
		else if(op == 2)
			return tre[u].sum2;
		else
			return tre[u].sum3;
	}
	int mid = tre[u].l + tre[u].r >> 1;
	int res = 0;
	pushdown(u);
	if(l <= mid)
		res = (res + query(lson, l, r, op)) % mod;
	if(r > mid)
		res = (res + query(rson, l, r, op)) % mod;
	return res;
}

void solve()
{
	while(cin >> n >> m, n || m)
	{
		memset(tre, 0, sizeof tre);
		build(1, 1, n);
		while(m--)
		{
			int opt, l, r, c;
			cin >> opt >> l >> r >> c;
			if(opt != 4)
				modify(1, l, r, c, opt);
			else
				cout << query(1, l, r, c) << endl;
		}
	}
}

signed main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);

	solve();
}