【最小生成树】一文学懂prim、kruskal算法

• 博主简介：努力学习的大一在校计算机专业学生，热爱学习和创作。目前在学习和分享：算法、数据结构、Java等相关知识。
• 博主主页： @是瑶瑶子啦
• 所属专栏: 算法 ；该专栏专注于蓝桥杯和ACM等算法竞赛🔥
• 近期目标：写好专栏的每一篇文章

🎊前言

首先，我们要了解什么是最小生成树

🌠树and图？
其实树也是一种特殊的图；无向、无环、联通 图，就是树。

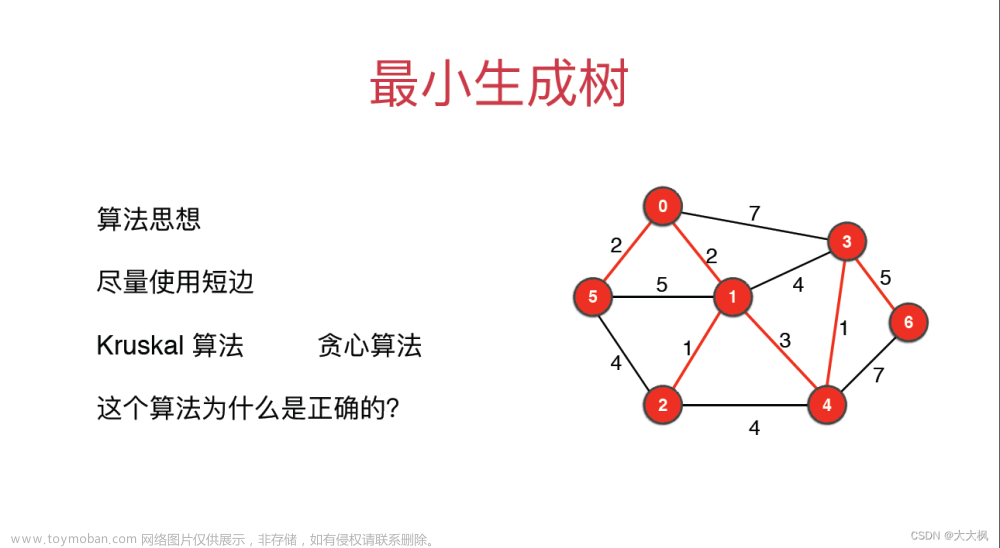
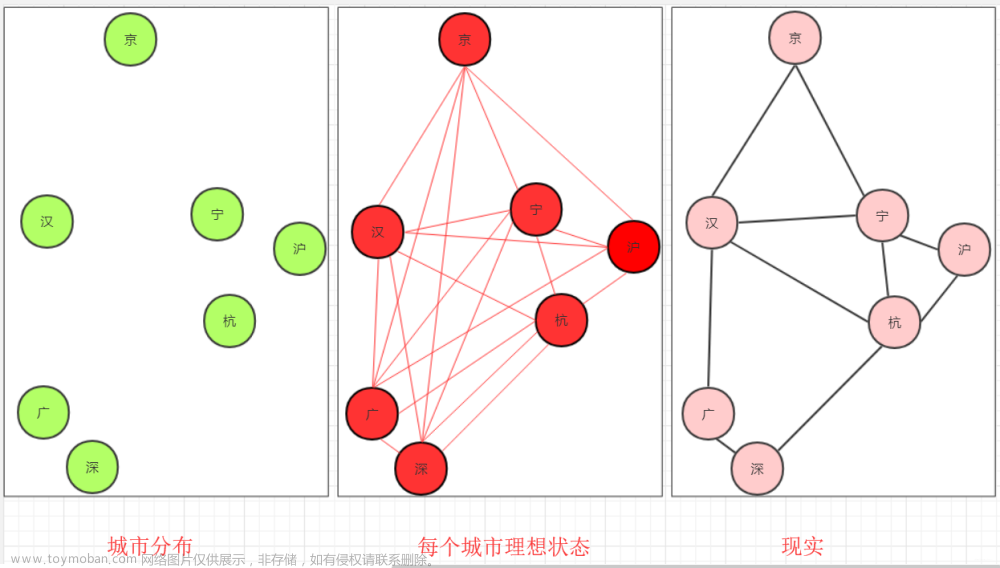
🌳最小生成树
求最小生成树，简单来说，就是让组成图的顶点，根据现有的边的关系，从图转换成一个特殊的图——树，光转换成树还不行，还要时这个特殊的图的所有边的权重加起来最小！这就是所谓的求最小生成树

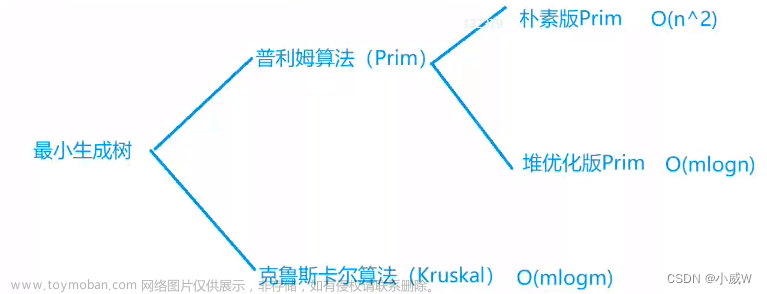
📌一、Prim算法

1.1：prim基本思想

每次将离连通部分的最近的点和点对应的边加入的连通部分，连通部分逐渐扩大，最后将整个图连通起来，并且边长之和最小。

• 📍首先一个dist数组，用于存储还为加入联通部分的点到联通部分的最短距离（绿色点表示未联通，红色表示已处于联通部分,紫色框中的是该点的dist值）；最开始肯定所有点的dist都是无穷大(INF = 0x3f3f3f3f)
  
• 💡关于dist数组的定义，这里再用图形的方式来解释一下。红色表示已经暂时确定的连通图（也就是之后确定完全之后的最小生成树），绿色的表示某一个点，该点可能有很多条边连接到该连通图（也可能不能联通，不能联通就置为INF）；取这些边中最小的一条，即为dist[E]就代表E点到联通图的最短距离
  
• 📍定义好dist数组并且初始化后，随便挑一个点都行，加入连通图集合，这里我们选入一号点加入集合，把dist[1]是0（后面代码并没有把第一个选中的点的dist置为0其实，直接不累加就行，第一个点的dist不用更新，也没有必要；注意在后续点进行时迭代时，必须先累加其dist，再更新，这点下面还会详细说）
  
• 📍用找到的距离联通图距离最短的（未在联通图内，且dist最小）的该点，用该点遍历该点所连接的边的顶点，更新相邻点的dist!(和dijkstra有点像，先找到距离某个地方最近的一个点，用该点去更新相邻的其他点！）
  
• 📍更新完后，下次迭代，先找到距离连通图距离最短的（这里就是2），用2更新相邻点到连通图的距离，再把2也加入联通图阵营
• 📍不断进行上述找最小、借东风（以一点更新相邻点、加入联通图阵营（是不是和Dijkstra很像！不同的就在于，找最小和更新的部分）最后就形成了一个完整的、边数相加最小的联通图（即最小生成树）
  
  

1.2：prim原理浅谈

树是一种特殊的图，一个无向联通图且不包含回路（即不存在环），那么就是一个树
以下是菜鸟瑶瑶子的拙见

• 💡如何保证是个树？
  首先一定不能有环，而且还得联通。这两点保证了，就是树。保证联通好说，在该算法中，我们把顶点一个一个依次往联通图上去连接，这个过程顺利进行就保证肯定是联通的。如何保证没有环呢？可以这样理解，一个顶点有两只手，一个点加入联通图，那么一只手就和联通图连上了，如果再把该点再次加入联通图（另一只手也连上），那势必会存在环。而该算法保证每次往联通图中加的点都是不在联通图中的。这就保证了在联通图中的点，一只手连着联通图，另一只手空着或者连着联通图外的点。这样一来，就不会存在环了

• 💡如何保证边的和最小？
  其实是贪心策略。局部最优，我们每次往联通图中加入的点，都是离联通图最近的点。局部最优解构成全局最优解（因为目前还没学到贪心，要真说原理什么的，我目前还证明不了，只能凭着感觉去意会，感兴趣的同学可以上C站或者百度搜搜看）

1.3：核心模板代码

from acwing(侵删）
时间复杂度是 O(n2+m)O(n2+m), n 表示点数，m 表示边数

时间复杂度是 O(n2+m)O(n2+m), nn 表示点数，mm 表示边数
int n;      // n表示点数
int g[N][N];        // 邻接矩阵，存储所有边
int dist[N];        // 存储其他点到当前最小生成树的距离
bool st[N];     // 存储每个点是否已经在生成树中


// 如果图不连通，则返回INF(值是0x3f3f3f3f), 否则返回最小生成树的树边权重之和
int prim()
{
    memset(dist, 0x3f, sizeof dist);

    int res = 0;
    for (int i = 0; i < n; i ++ )
    {
        int t = -1;
        for (int j = 1; j <= n; j ++ )
            if (!st[j] && (t == -1 || dist[t] > dist[j]))
                t = j;

        if (i && dist[t] == INF) return INF;

        if (i) res += dist[t];
        st[t] = true;

        for (int j = 1; j <= n; j ++ ) dist[j] = min(dist[j], g[t][j]);
    }

    return res;
}

1.4:模板题训练+详细注释题解

858. Prim算法求最小生成树

给定一个 n 个点 m 条边的无向图，图中可能存在重边和自环，边权可能为负数。

求最小生成树的树边权重之和，如果最小生成树不存在则输出 impossible。

给定一张边带权的无向图 G=(V,E)，其中 V 表示图中点的集合，E 表示图中边的集合，n=|V|，m=|E|。

由 V 中的全部 n 个顶点和 E 中 n−1 条边构成的无向连通子图被称为 G 的一棵生成树，其中边的权值之和最小的生成树被称为无向图 G
的最小生成树。

输入格式

第一行包含两个整数 n 和 m。

接下来 m 行，每行包含三个整数 u,v,w，表示点 u 和点 v 之间存在一条权值为 w 的边。

输出格式

共一行，若存在最小生成树，则输出一个整数，表示最小生成树的树边权重之和，如果最小生成树不存在则输出 impossible。

数据范围

1≤n≤500, 1≤m≤105, 图中涉及边的边权的绝对值均不超过 10000。

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 510, INF = 0x3f3f3f3f;

int n,m;//点和边数
int g[N][N];//用于存边
int dist[N];//存当前点到联通图的最小距离
bool st[N];//判断该点是否在联通图中

int prim(){
    memset(dist,0x3f, sizeof dist);
    
    int res = 0;
    
    for(int i = 0;i <= n; i++){
        int t = -1;
        for(int j = 1; j <=n; j++)
            if(!st[j]&&(t == -1 || dist[t] > dist[j]))
                t = j;
        
        if(i && dist[t] == INF) return INF;
        
        if(i) res += dist[t];
        st[t] = true;
        
        //借东风
        for(int j = 1; j <= n; j ++) dist[j] = min (dist[j],g[t][j]);
    }
    
    return res;
}

int main(){
    scanf("%d%d",&n,&m);
    
    memset(g,0x3f, sizeof g);
    
    while(m--){
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        g[a][b] = g[b][a] = min(g[a][b],c);//存边，无向图，记得存两条边，且要判重
    }
    int t = prim();
    
    if(t == INF) puts("impossible");
    
    else printf("%d\n",t);
    
    return 0;
}

💡注意点

• 与dijkstra不同，prim需要迭代n次（因为dijkstra已经确定的起点，少的那一次就少在，dijkstra在循环前就把源点加入集合了！）
• 最小生成树是针对无向图的，所以在读入边的时候，需要赋值两次（且注意判重！）
• 要先把这次迭代选中的点的dist累加，再已该点更新与之相连的点，避免t有自环（在更新的适合dist[t] = 0,后面再累加进答案就不对了），影响答案的正确性。后更新不会影响后面的结果么？不会的，因为dist[i]为i到集合S的距离，当t放入集合后，其dist[t]就已经没有意义了，再更新也不会影响答案的正确性

📌二、kruskal算法

2.1基本思路

核心思想：:所有边能小则小，算法的实现方面要用到***并查集***判断两点是否在同一集合

• 首先，将所有边，按照权重大小，从小到大排序

• 构造一个只含 n 个顶点、而边集为空的子图，把子图中各个顶点看成各棵树上的根结点

• 从边集 E 中选取一条权值最小的边，若该条边的两个顶点分属不同的树（保证了最后是联通且没有环的图，即树），则将其加入子图；即把两棵树合成一棵树；

• 反之，若该条边的两个顶点已落在同一棵树上，则不可取（取了的话会形成环！），而应该取下一条权值最小的边再试之

• 依次类推，直到森林中只有一棵树，也即子图中含有 n-1 条边为止。

2.2:具体步骤/实现

1. 将图中所有边对象(边长、两端点)依次加入集合(优先队列)q1中（或者用数组存边，之后再按权重排序一下，本质都是一样的，让所有的边按升序存储）。初始所有点相互独立（都是不同树的根节点）

2. 取出存储边的集合中的最小边，判断边的两点是否联通。（是否同属于一棵树/集合/连通块

3. 如果联通说明两个点已经有其它边将两点联通了，跳过（不然就形成自环啦），如果不连通，则使用并查集合并，将两个顶点合并

4. 重复2，3操作直到存储边的集合为空。此时被选择的边构成最小生成树。

2.3算法模板

from acwing(侵删）
时间复杂度是 O(mlogm)O(mlogm), n 表示点数，m 表示边数

int n, m;       // n是点数，m是边数
int p[N];       // 并查集的父节点数组

struct Edge     // 存储边
{
    int a, b, w;

    bool operator< (const Edge &W)const
    {
        return w < W.w;
    }
}edges[M];

int find(int x)     // 并查集核心操作
{
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int kruskal()
{
    sort(edges, edges + m);

    for (int i = 1; i <= n; i ++ ) p[i] = i;    // 初始化并查集

    int res = 0, cnt = 0;
    for (int i = 0; i < m; i ++ )
    {
        int a = edges[i].a, b = edges[i].b, w = edges[i].w;

        a = find(a), b = find(b);
        if (a != b)     // 如果两个连通块不连通，则将这两个连通块合并
        {
            p[a] = b;
            res += w;
            cnt ++ ;
        }
    }

    if (cnt < n - 1) return INF;
    return res;
}

2.4：模板题目

859. Kruskal算法求最小生成树

给定一个 n 个点 m 条边的无向图，图中可能存在重边和自环，边权可能为负数。

求最小生成树的树边权重之和，如果最小生成树不存在则输出 impossible。

给定一张边带权的无向图 G=(V,E)，其中 V 表示图中点的集合，E 表示图中边的集合，n=|V|，m=|E|。

由 V 中的全部 n 个顶点和 E 中 n−1 条边构成的无向连通子图被称为 G 的一棵生成树，其中边的权值之和最小的生成树被称为无向图 G
的最小生成树。

输入格式

第一行包含两个整数 n 和 m。

接下来 m 行，每行包含三个整数 u,v,w，表示点 u 和点 v 之间存在一条权值为 w 的边。

输出格式

共一行，若存在最小生成树，则输出一个整数，表示最小生成树的树边权重之和，如果最小生成树不存在则输出 impossible。

数据范围

1≤n≤105, 1≤m≤2∗105, 图中涉及边的边权的绝对值均不超过 1000。

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 100010;
int res;
int p[N];//保存并查集

struct E{
    int a, b, w;
    //因为sort排序函数内部实现是通过小于号来实现的，所以这里需要重载小于号，保证是按边的权重进行排序
    bool operator < (const E& rhs){
        return this->w < rhs.w;
    }
}edge[N * 2];//因为是无向图，所以开两倍

int n,m;
int cnt;//cnt 负责记录当前有多少条边已经加入最终的联通图阵营，根据抽屉原理，加购n-1条边，就说明有n个点，就说明最小生成树已经构建完成

//并查集的核心代码，寻找祖宗节点
int find(int a){
    if(p[a] != a) p[a] = find(p[a]);
    return p[a];
}

//kruskal核心代码
void kruskal(){
    for (int i = 1; i <= m ; i++){//依次尝试加入每条边
        int pa = find(edge[i].a);//a-b边，得到点a所在集合
        int pb = find(edge[i].b);
        if(pa != pb){//a和b两个点暂时不在一个连通块，符合！
            res += edge[i].w;
            p[pa] = pb;//合并a,b两个集合
            cnt ++;//最终连通块的边数+1
        }
    }
}
int main(){
    cin >> n >> m;
    for(int i = 1; i <= n; i++) p[i] = i;//初始化并查集（每个点独立，属于自己的独立集合）
    //读入每条边
    for (int i = 1; i <= m; i++){
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        edge[i] = {a,b,c};
    }
    //对每条边，按照权重进行从小到大排序（升序
    sort(edge+1, edge + m +1);//[ edge[1], edge[m+1] ) 左闭右开
    kruskal();
    if(cnt < n-1){ //说明最终联通图中并没有把所有点都连接起来，说明不能构建最小生成树
        cout << "impossible";
        return 0;
    }
    
    cout << res;
    
    return 0;
}
    

文章来源地址https://www.toymoban.com/news/detail-424579.html

• Java岛冒险记【从小白到大佬之路】
  
• LeetCode每日一题–进击大厂
• 算法

到了这里，关于【最小生成树】一文学懂prim、kruskal算法的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！