目录
两样本和多样本的Brown-Mood中位数检验
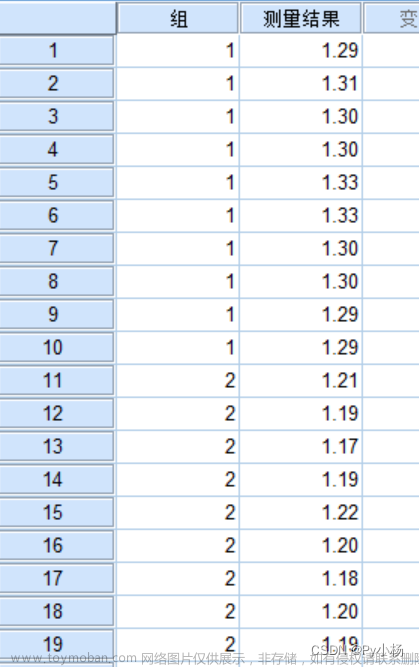
例3.1我国两个地区一些(分别为17个和15个)城镇职工的工资(元):
Wilcoxon(Mann-Whitney)秩和检验及有关置信区间
例3.1我国两个地区一些(分别为17个和15个)城镇职工的工资(元):
Kruskal-Wallis秩和检验
例4.1在一项健康实验中,三人组有三种生活方式,他们的减肥效果如下表:
-
两样本和多样本的Brown-Mood中位数检验
定义:零假设:H0:Mx=My,备择假设:H1:Mx<My.
如果H0成立,两样本混合中位数Mxy可以均匀的分开X和Y两个样本,检验关注A的数值,A的意义是样本X混合中位数右侧的个数,如果A很大,则表示样本X的中位数明显大于样本Y的;如果A很小,则表示样本Y的中位数明显大于样本X的。
例3.1我国两个地区一些(分别为17个和15个)城镇职工的工资(元):
地区1:6864 7304 7477 7779 7895 8348 8461 9553 9919 10073 10270 11581 13472 13600 13962 15019 17244
地区2:10276 10533 10633 10837 11209 11393 11864 12040 12642 12675 13199 13683 14049 14061 16079
人们想要知道这两个地区平均城镇职工工资的中位数是否一样.
答:由题里的数据可制作下图:
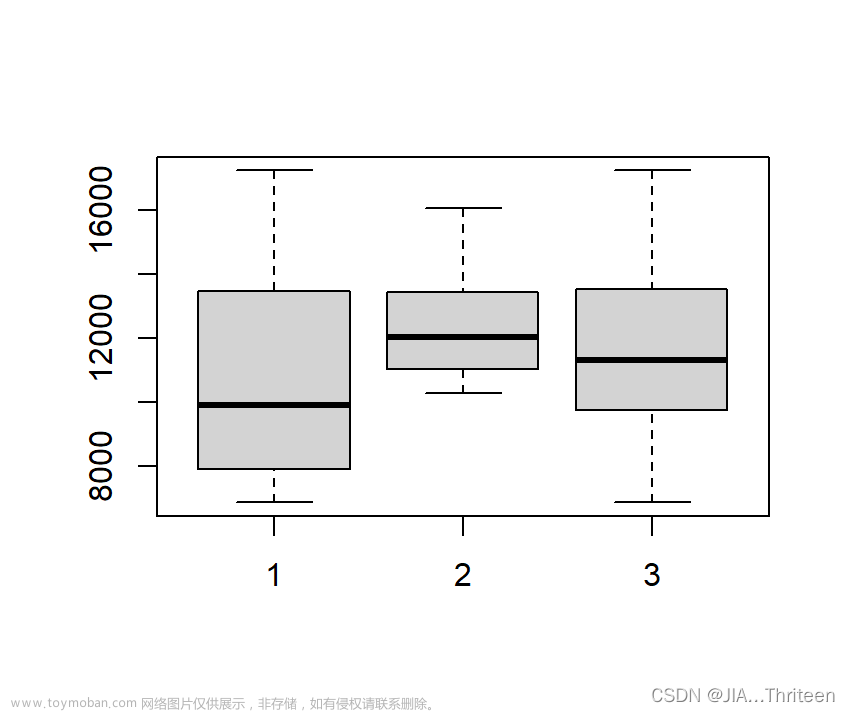
箱线图从左到右依次代表地区1,地区2和混合样本的数据
令地区1的样本数据中位数为Mx,地区2的为My,混合样本数据的中位数为Mxy.
零假设:H0:Mx=My,备择假设:H1:Mx<My.
如果H0成立,则混合样本的中位数Mxy在地区1、地区2的两个样本中,大于或小于Mxy应该大体一样。
由数据算得Mxy=11301,用两样本数据和Mxy比较后得到下表1:
| 地区1(X) |
地区二(Y) |
总和 |
|
| 大于Mxy的数目 |
a=6 |
b=10 |
t=16 |
| 小于Mxy的数目 |
m-a=11 |
n-b=5 |
N-t=16 |
| 总和 |
m=17 |
n=15 |
N=32 |
令A表示列表中a的取值,在m,n和t固定时,A的分布在H0下的超几何分布(m<k)为:
P(A=k)=mknt-km+nt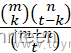
Brown-Mood中位数检验的基本内容(表2):
| 零假设:H0 |
备择假设:H1 |
检验统计量 |
P值 |
| H0:Mx=My |
H1:Mx<My |
A |
P(X≥a) |
| H0:Mx=My |
H1:Mx>My |
A |
P(X≤a) |
| H0:Mx=My |
H1:Mx≠My |
A |
2min(P(X≥a),P(X≤a)) |
由表1数据可知,p值为P(X≤a)=P(X≤6)=0.07780674(由r算得),根据这个p值,按照显著性水平0.05,无法拒绝原假设。也就是两个地区平均城镇职工工资的中位数是一样的。

以此类推,可以求出下表3:
| P(X≥6) |
0.9221933 |
| P(X≤6) |
0.07780674 |
| 2min(P(X≥6),P(X≤6)) |
0.1556135 |
在零假设下,在大样本时,可以从超几何分布的均值和标准差的表达式来得到正态近似统计量为:
Z=A±0.5-mt/Nmnt(N-t)/N3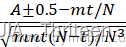 ~N(0,1)
~N(0,1)
对于双边备则检验(H1:Mx≠My),在大样本情况下,可以用检验统计量
K=2a-m2(m+n)mn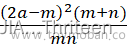
它近似服从自由度为1的卡方分布,当K=3.137255,p值为0.0765225.
由于0.0765225>0.05所以我们有没有充分理由拒绝H0 ,即不能说A组学生比B组学生算得更快。
,即不能说A组学生比B组学生算得更快。
R代码:文章来源地址https://www.toymoban.com/news/detail-424638.html
x=c(6864,7304,7477,7779,7895,8348,8461,9553,9919,10073,10270,11581,13472,13600,13962,15019,17244)
y=c(10276,10533,10633,10837,11209,11393,11864,12040,12642,12675,13199,13683,14049,14061,16079)
z=c(6864,7304,7477,7779,7895,8348,8461,9553,9919,10073,10270,11581,13472,13600,13962,15019,17244,10276,10533,10633,10837,11209,11393,11864,12040,12642,12675,13199,13683,14049,14061,16079)
boxplot(x,y,z)
median(z, na.rm = FALSE)
a=6
b=10
m=17
n=15
phyper(a,m,n,a+b)
1-phyper(a,m,n,a+b)
1-phyper(a-1,m,n,(m+n)-(a+b))
2*phyper(a,m,n,a+b)
pnorm((a+0.5-m*(a+b)/(m+n))/sqrt(m*n*(a+b)*(m+n-(a+b))/(m+n)^3))-
Wilcoxon(Mann-Whitney)秩和检验及有关置信区间
定义:Wilcoxon(Mann-Whitney)秩和检验是Brown-Mood中位数检验的升级版,假设两个总体分布有类似的形状,不假定对称。
X1,X2,…,Xm~F(X-μ1);Y1,Y2,…,Yn~(Y-μ2)
零假设:H0:μ1=μ2,备择假设:H1:μ1≠μ2
例3.1我国两个地区一些(分别为17个和15个)城镇职工的工资(元):
地区1:6864 7304 7477 7779 7895 8348 8461 9553 9919 10073 10270 11581 13472 13600 13962 15019 17244
地区2:10276 10533 10633 10837 11209 11393 11864 12040 12642 12675 13199 13683 14049 14061 16079
人们想要知道这两个地区平均城镇职工工资的中位数是否一样.
答:令地区1的样本数据中位数为Mx,地区2的为My,混合样本数据的中位数为Mxy.
零假设:H0:Mx=My,备择假设:H1:Mx<My.
下面是两个地区混合样本的秩:
| X |
6864 |
7304 |
7477 |
7779 |
7895 |
8348 |
8461 |
9553 |
9919 |
| 秩 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| X |
10073 |
10270 |
11581 |
13472 |
13600 |
13962 |
15019 |
17244 |
|
| 秩 |
10 |
11 |
18 |
24 |
25 |
27 |
30 |
32 |
|
| Y |
10276 |
10533 |
10633 |
10837 |
11209 |
11393 |
11864 |
12040 |
12642 |
| 秩 |
12 |
13 |
14 |
15 |
16 |
17 |
19 |
20 |
21 |
| Y |
12675 |
13199 |
13683 |
14049 |
14061 |
16079 |
|||
| 秩 |
22 |
23 |
26 |
28 |
29 |
31 |

可以得出Wy=306,Wx=222,Wxy=186,Wyx=69.
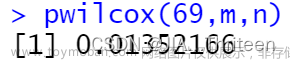
对于备则检验H1:Mx<My,得到p值为0.0135。因此,对于高于0.015的置信区间水平都可以拒绝零假设。
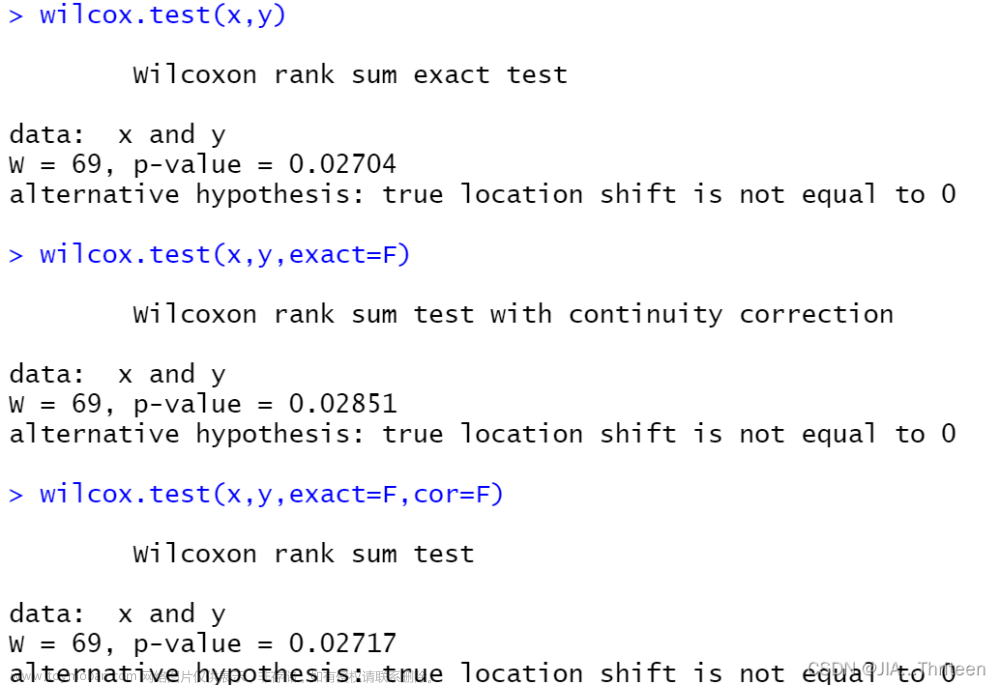
对于双边备择假设H1:Mx≠My,得到p值为0.0270,是上面单边检验的两倍;若用连续修正的正态近似,得到p值为0.0285,;若不加连续改正量,得到p值为0.0272.

对于备择假设H1:Mx<My,若用连续修正的正态近似,得到p值为0.0143,;若不加连续改正量,得到p值为0.0136.
由于以上计算的所有p值,均小于0.05,所以我们有充分的理由拒绝原假设,即地区1的中位数比地区2小。
Mx-My的点估计和区间估计:

由上述代码运行结果知,Mx-My的点估计为-2479.

由上述代码运行结果知,Mx-My的(1-α)置信区间为(-3916,-263)。
R代码:
x=c(6864,7304,7477,7779,7895,8348,8461,9553,9919,10073,10270,11581,13472,13600,13962,15019,17244)
y=c(10276,10533,10633,10837,11209,11393,11864,12040,12642,12675,13199,13683,14049,14061,16079)
m=length(x);n=length(y);m;n;
Wxy=sum(outer(y,x,"-")>0);Wxy
Wyx=sum(outer(x,y,"-")>0);Wyx
pwilcox(69,m,n)
wilcox.test(x,y)
wilcox.test(x,y,exact=F)
wilcox.test(x,y,exact=F,cor=F)
wilcox.test(x,y,exact=F,alt="less")
wilcox.test(x,y,exact=F,alt="less",cor=F)
median(outer(x,y,"-"))
D=sort(as.vector(outer(x,y,"-")))
qwilcox(0.025,m,n)
D[76]
D[m*n+1-76]-
Kruskal-Wallis秩和检验
定义:Kruskal-Wallis秩和检验根据所有数据从小到大排序,算出每个数据的秩。其中Ri为每组的秩和,ni为每组的样本个数。当每组样本中的观察数目有5个或5个以上,则样本统计量 KWC 的分布与自由度为k-1的卡方分布非常接近。因此,KW统计量可利用卡方分布进行检验。
KW=组间平方和/全体样本的秩方差
如果样本中存在结值(数据相同秩值的个数),则校正系数C=1-Σ(τi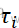 ^3-τi
^3-τi )/n^3-n,其中τi
)/n^3-n,其中τi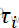 等于第j个结值的个数,调整后的KWc=KW/C.
等于第j个结值的个数,调整后的KWc=KW/C.
Kruskal-Wallis统计量:
H=12N(N-1)i=1kni(Ri-R)2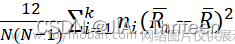 =12N(N-1)i=1kRi2ni-3(N+1)
=12N(N-1)i=1kRi2ni-3(N+1)
例4.1在一项健康实验中,三人组有三种生活方式,他们的减肥效果如下表:
| 生活方式 |
1 |
2 |
3 |
| 一个月后减少的重量(单位500g) |
3.7 |
7.3 |
9.0 |
| 3.7 |
5.2 |
4.9 |
|
| 3.0 |
5.3 |
7.1 |
|
| 3.9 |
5.7 |
8.3 |
|
| 2.7 |
6.5 |
||
| ni= |
5 |
5 |
4 |
人们想知道从这个数据能否得出他们的减肥效果(位置参数)是一样的。
答:假定k个样本有相似的连续正态分布,而且所有的观测值在样本内和样本之间是独立的,我们假定k个独立样本有连续的分布函数F1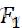 ,…, Fk
,…, Fk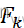 .我们设
.我们设
零假设H0:F1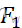 (X)=…=Fk
(X)=…=Fk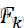 (X)=F(X);备择假设H1:Fi
(X)=F(X);备择假设H1:Fi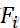 (X)=F(X-θi
(X)=F(X-θi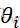 ),i=1,…,k
),i=1,…,k
这里F是某连续分布函数,而且这些位置参数θi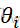 并不全部相同。
并不全部相同。
假定有k个样本,各样本的样本量为ni,i=1,…,k.那么,观测值可以写成下面的线性模型:xij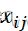 =μ+θi
=μ+θi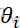 +εij
+εij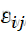 ,j=1,…, ni
,j=1,…, ni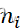 及 i=1,…,k,误差是独立同分布的.
及 i=1,…,k,误差是独立同分布的.
我们要检验的是H0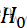 : θ1
: θ1 =θ2
=θ2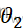 =…=θk
=…=θk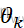 等价于Ha
等价于Ha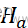 :H0
:H0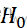 的诸等式中至少有一个不成立。
的诸等式中至少有一个不成立。
由题中数据所画箱线图如下:
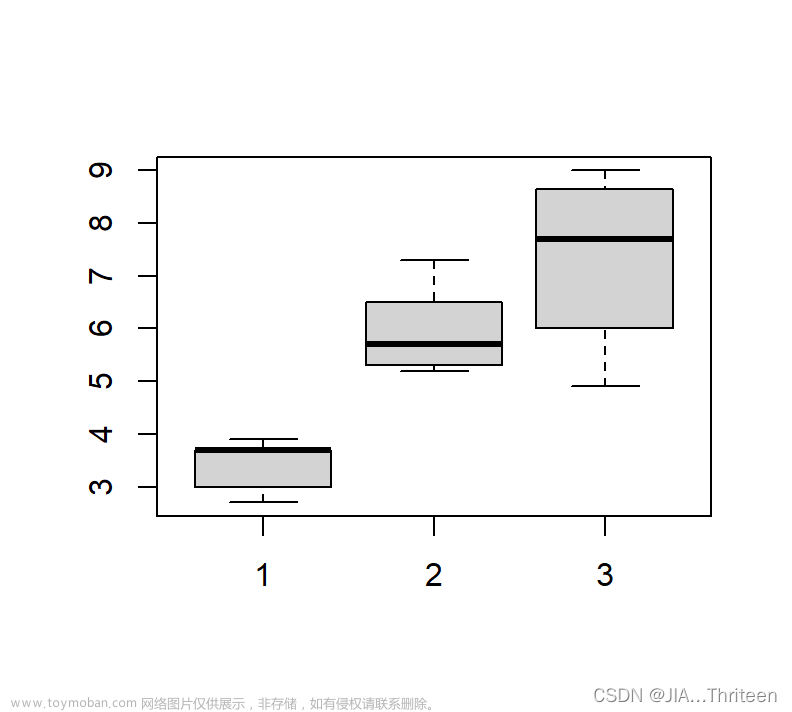

由上述代码运行结果知p=0.00895<0.05,故我们有充分理由拒绝H0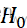 ,即他们的减肥效果,即位置参数是不一样的。文章来源:https://www.toymoban.com/news/detail-424638.html
,即他们的减肥效果,即位置参数是不一样的。文章来源:https://www.toymoban.com/news/detail-424638.html
R代码:
a=c(3.7,3.7,3.0,3.9,2.7)
b=c(7.3,5.2,5.3,5.7,6.5)
c=c(9.0,4.9,7.1,8.3)
boxplot(a,b,c)
m1=length(a)
m2=length(b)
m3=length(c)
m<-m1+m2+m3
library(fBasics)
d=c(a,b,c)
e=c(1,1,1,1,1,2,2,2,2,2,3,3,3,3)
kruskal.test(d,e)到了这里,关于非参数统计:两样本和多样本的Brown-Mood中位数检验;Wilcoxon(Mann-Whitney)秩和检验及有关置信区间;Kruskal-Wallis秩和检验的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!