实验4 图的应用问题给定n个村庄之间的交通图，现计划在n个村庄中选定一个村庄建造一所医院，请设计方案解决问题-Toy模板网

这篇具有很好参考价值的文章主要介绍了实验4 图的应用问题给定n个村庄之间的交通图，现计划在n个村庄中选定一个村庄建造一所医院，请设计方案解决问题。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

数据结构的某次编程实验

【问题描述】

给定n个村庄之间的交通图，现计划在n个村庄中选定一个村庄建造一所医院，请设计方案解决如下问题：
（1）求出该医院应建在哪个村庄，才能使距离最远的村庄到医院的路程最短；
（2）求出该医院应建在哪个村庄，能使其它所有村庄到医院的路径总和最短。

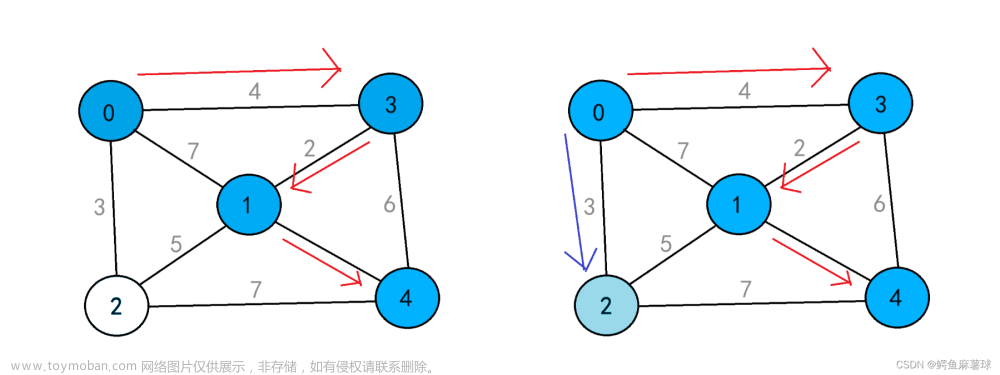
对于如上所示的无向图，设置输入形式如下：

5 //结点个数
A B C D E//输入多个结点值，每个值之间用一个空格隔开
6 //边个数
A B 5 //第1条边的顶点和权值，中间用一个空格隔开
A C 6 //第2条边的顶点和权值，中间用一个空格隔开
A D 3 //第3条边的顶点和权值，中间用一个空格隔开
D E 10 //第4条边的顶点和权值，中间用一个空格隔开
E C 15 //第5条边的顶点和权值，中间用一个空格隔开
C B 7 //第6条边的顶点和权值，中间用一个空格隔开

【输出形式】

D //D村庄1
A //村庄2

实验4 图的应用问题给定n个村庄之间的交通图，现计划在n个村庄中选定一个村庄建造一所医院，请设计方案解决问题

【样例输入】

5
A B C D E
6
A B 5
A C 6
A D 3
D E 10
E C 15
C B 7

【样例输出】

D
A

注：本题运用Dijkstra算法，Dijkstra算法讲解请参考我的另一博文->[点击此处跳转]文章来源地址https://www.toymoban.com/news/detail-424748.html

C++代码实现

#include<iostream>
using namespace std;
#include<limits.h>   //包含int等类型的最值，若两点不连通则该两点的虚边权值为INT_MAX
struct graph {
	char vertlist[100];   //节点名称（如A B C...）
	int edgelist[100][100];   //邻接矩阵
	int n, e;   // n 为nodes' count, e 为edges' count
};
struct table {   //标记当前顶点状态
	bool visited;   //标记当前顶点是否已被访问
	int distance, path;   //当前顶点与各个顶点的最小距离（distance）和经过的顶点
};
void CreateGraph(graph*& g) {
	g = new graph;
	cin >> g->n;   //输入顶点个数
	for (int i = 1; i <= g->n; i++) {
		cin >> g->vertlist[i];   //输入顶点名称（如A B C...）
		for (int j = 1; j <= g->n; j++) {   //初始化邻接矩阵
			if (i != j) g->edgelist[i][j] = INT_MAX;
			else g->edgelist[i][j] = 0;
		}
	}
	cin >> g->e;   //输入边个数
	char temp1, temp2;
	int weight, adj1, adj2;
	for (int i = 1; i <= g->e; i++) {   //将输入的信息转为邻接矩阵储存
		cin >> temp1 >> temp2 >> weight;
		for (int j = 1; j <= g->n; j++) {
			if (g->vertlist[j] == temp1) adj1 = j;
			if (g->vertlist[j] == temp2) adj2 = j;
		}
		g->edgelist[adj1][adj2] = weight;
		g->edgelist[adj2][adj1] = weight;   //无向图需交换邻接点再次录入边信息
	}
}
int Findmin(graph* g, table* t) {   //找到距离最进的顶点
	int min = INT_MAX, adjmin;
	for (int i = 1; i <= g->n; i++)
		if (!t[i].visited && t[i].distance < min) {
			min = t[i].distance;
			adjmin = i;
		}
	return adjmin;
}
void Dijkstra(graph* g, table* t, int flag) {   //从flag顶点出发，求到各个顶点的距离distance（Dijkstra算法）
	for (int i = 1; i <= g->n; i++) {
		t[i].distance = g->edgelist[flag][i];
		t[i].visited = false;
		t[i].path = flag;
	}
	t[flag].visited = true;
	int sum, adjmin;
	for (int i = 1; i < g->n; i++) {   //因为flag顶点已被选出，因此还需选出n-1个顶点
		adjmin = Findmin(g, t);
		t[adjmin].visited = true;
		for (int j = 1; j <= g->n; j++)
			if (!t[j].visited && g->edgelist[adjmin][j] < INT_MAX) {   //注：无向图一定要判断 g->edgelist[adjmin][j]<INT_MAX
				sum = t[adjmin].distance + g->edgelist[adjmin][j];
				if (sum < t[j].distance) {
					t[j].distance = sum;
					t[j].path = adjmin;
				}
			}
	}
}
int main() {
	graph* g;
	CreateGraph(g);
	table t[100][100];
	for (int i = 1; i <= g->n; i++)
		Dijkstra(g, t[i], i);   //从i顶点出发，求到各个顶点的距离distance，存储在t[i]里
	int farthest[100],tempfar;   //farthest[i]为储存从第i顶点出发到最远顶点的最短距离
	for (int i = 1; i <= g->n; i++) {
		tempfar = 0;
		for (int j = 1; j <= g->n; j++)
			if (tempfar < t[i][j].distance)
				tempfar = t[i][j].distance;
		farthest[i] = tempfar;
	}
	int min = INT_MAX, adjmin;   //adjmin为最小值的下标
	for(int i=1;i<=g->n;i++)
		if (min > farthest[i]) {
			min = farthest[i];
			adjmin = i;   //adjmin为到最远顶点的最短距离的最小值的出发顶点下标
		}
	cout << g->vertlist[adjmin] << endl;   //输出第一问题的解
	int sum[100] = { 0 };   //从i顶点出发，求到各个顶点的最短距离之和
	for (int i = 1; i <= g->n; i++)
		for (int j = 1; j <= g->n; j++)
			sum[i] += t[i][j].distance;
	min = INT_MAX;   //min重置为很大的数
	for (int i = 1; i <= g->n; i++)   //找到以adjmin顶点出发路径总和最短
		if (min > sum[i]) {
			min = sum[i];
			adjmin = i;
		}
	cout << g->vertlist[adjmin] << endl;   //输出第二问题的解
	return 0;
}