智能优化算法:金枪鱼群优化算法
摘要:金枪鱼群优化算法(Tuna swarm optimization,TSO),是于2021年提出的一种新型智能优化算法,该算法通过模拟金枪鱼群体的觅食行为,来对问题进行寻优。具有寻优能力强,收敛速度快等特点。
1.算法原理
1.1 初始化
与其他智能优化算法一样,金枪鱼种群在搜索空间内随机初始化。
X
i
i
n
t
=
r
a
n
d
⋅
(
u
b
−
l
b
)
+
l
b
,
i
=
1
,
2
,
⋯
,
N
P
(1)
\mathbf{X}_{i}^{\mathrm{int}}=\mathbf{r a n d} \cdot(\mathbf{u b}-\mathbf{l b})+\mathbf{l b}, i=1,2, \cdots, N P \tag{1}
Xiint=rand⋅(ub−lb)+lb,i=1,2,⋯,NP(1)
其中,
X
i
i
n
t
X_i^{int}
Xiint是第
i
i
i个个体的初始位置,
u
b
ub
ub和
l
b
lb
lb分别是搜索空间的上界和下界,
N
P
NP
NP是金枪鱼种群的数量,
r
a
n
d
rand
rand是一个均匀分布的[0,1]内的随机向量。
1.2 螺旋觅食
金枪鱼群通过形成紧密的螺旋来追逐猎物,除了追逐猎物,成群的金枪鱼还相互交换信息。每一条金枪鱼都跟在前一条鱼的后面,因此可以在相邻的金枪鱼之间共享信息。基于上述原理,螺旋觅食策略的数学公式如下:
X
i
t
+
1
=
{
α
1
⋅
(
X
best
t
+
β
⋅
∣
X
best
t
−
X
i
t
∣
)
+
α
2
⋅
X
i
t
,
i
=
1
α
1
⋅
(
X
best
t
+
β
⋅
∣
X
best
t
−
X
i
t
∣
)
+
α
2
⋅
X
i
−
1
t
,
i
=
2
,
3
,
⋯
,
N
P
(2)
\mathbf{X}_{i}^{t+1}=\left\{\begin{array}{ll} \alpha_{1} \cdot\left(X_{\text {best }}^{t}+\beta \cdot\left|X_{\text {best }}^{t}-\mathbf{X}_{i}^{t}\right|\right)+\alpha_{2} \cdot \mathbf{X}_{i}^{t}, & i=1 \\ \alpha_{1} \cdot\left(X_{\text {best }}^{t}+\beta \cdot\left|X_{\text {best }}^{t}-\mathbf{X}_{i}^{t}\right|\right)+\alpha_{2} \cdot \mathbf{X}_{i-1}^{t}, & i=2,3, \cdots, N P \end{array}\right.\tag{2}
Xit+1={α1⋅(Xbest t+β⋅∣Xbest t−Xit∣)+α2⋅Xit,α1⋅(Xbest t+β⋅∣Xbest t−Xit∣)+α2⋅Xi−1t,i=1i=2,3,⋯,NP(2)
α 1 = a + ( 1 − a ) ⋅ t t max (3) \alpha_{1}=a+(1-a) \cdot \frac{t}{t_{\max }}\tag{3} α1=a+(1−a)⋅tmaxt(3)
α 2 = ( 1 − a ) − ( 1 − a ) ⋅ t t max (4) \alpha_{2}=(1-a)-(1-a) \cdot \frac{t}{t_{\max }} \tag{4} α2=(1−a)−(1−a)⋅tmaxt(4)
β = e b l ⋅ cos ( 2 π b ) (5) \beta=e^{b l} \cdot \cos (2 \pi b) \tag{5} β=ebl⋅cos(2πb)(5)
l = e 3 cos ( ( ( t max + 1 ) / t ) − 1 ) π ) (6) l=e^{\left.3 \cos \left(\left(\left(t_{\max }+1\right) / t\right)-1\right) \pi\right)} \tag{6} l=e3cos(((tmax+1)/t)−1)π)(6)
X
i
t
+
1
X_i^{t+1}
Xit+1是第
t
+
1
t+1
t+1次迭代的第
i
i
i个个体,
X
b
e
s
t
t
X_{best}^t
Xbestt是当前最佳个体(食物),
α
1
\alpha_1
α1 和
α
2
\alpha_2
α2是控制个体向最佳个体和前一个个体移动趋势的权重系数,
a
a
a是一个常数,用于确定金枪鱼在初始阶段跟随最佳个体和前一个体的程度,
t
t
t表示当前迭代次数,
t
m
a
x
t_{max}
tmax表示最大迭代次数,
b
b
b是均匀分布在0到1之间的随机数。当最优个体找不到食物时,盲目跟随最优个体觅食不利于群体觅食。因此,考虑在搜索空间中生成一个随机坐标,作为螺旋搜索的参考点。它使每个个体都能在更广阔的空间里探索,并使TSO具有全局探索能力。具体的数学模型描述如下:
X
i
t
+
1
=
{
α
1
⋅
(
X
rand
t
+
β
⋅
∣
X
rand
t
−
X
i
t
∣
)
+
α
2
⋅
X
i
t
,
i
=
1
α
1
⋅
(
X
rand
t
+
β
⋅
∣
X
rand
t
−
X
i
t
∣
)
+
α
2
⋅
X
i
−
1
t
,
i
=
2
,
3
,
⋯
,
N
P
(7)
\mathbf{X}_{i}^{t+1}=\left\{\begin{array}{ll} \alpha_{1} \cdot\left(X_{\text {rand }}^{t}+\beta \cdot\left|X_{\text {rand }}^{t}-\mathbf{X}_{i}^{t}\right|\right)+\alpha_{2} \cdot \mathbf{X}_{i}^{t}, & i=1 \\ \alpha_{1} \cdot\left(X_{\text {rand }}^{t}+\beta \cdot\left|X_{\text {rand }}^{t}-\mathbf{X}_{i}^{t}\right|\right)+\alpha_{2} \cdot \mathbf{X}_{i-1}^{t}, & i=2,3, \cdots, N P \end{array}\right. \tag{7}
Xit+1={α1⋅(Xrand t+β⋅∣Xrand t−Xit∣)+α2⋅Xit,α1⋅(Xrand t+β⋅∣Xrand t−Xit∣)+α2⋅Xi−1t,i=1i=2,3,⋯,NP(7)
其中,
X
r
a
n
d
t
X_{rand}^t
Xrandt是搜索空间中随机生成的参考点。启发式算法通常在早期阶段进行广泛的全局探索,然后逐渐过渡到精确的局部开发。因此,随着迭代次数的增加,TSO将螺旋觅食的参考点从随机个体更改为最优个体。综上所述,螺旋觅食策略的最终数学模型如下:
X
i
t
+
1
=
{
{
α
1
⋅
(
X
rand
t
+
β
⋅
∣
X
rand
t
−
X
i
t
∣
)
+
α
2
⋅
X
i
t
,
i
=
1
α
1
⋅
(
X
rand
t
+
β
⋅
∣
X
rand
t
−
X
i
t
∣
)
+
α
2
⋅
X
i
−
1
t
,
i
=
2
,
3
,
⋯
,
N
P
,
if rand
<
t
t
max
{
α
1
⋅
(
X
best
t
+
β
⋅
∣
X
best
t
−
X
i
t
∣
)
+
α
2
⋅
X
i
t
,
i
=
1
α
1
⋅
(
X
best
t
+
β
⋅
∣
X
best
t
−
X
i
t
∣
)
+
α
2
⋅
X
i
−
1
t
,
i
=
2
,
3
,
⋯
,
N
P
,
if rand
≥
t
t
max
(8)
\mathbf{X}_{i}^{t+1}=\left\{\begin{array}{ll} \left\{\begin{array}{ll} \alpha_{1} \cdot\left(X_{\text {rand }}^{t}+\beta \cdot\left|X_{\text {rand }}^{t}-\mathbf{X}_{i}^{t}\right|\right)+\alpha_{2} \cdot \mathbf{X}_{i}^{t}, & i=1 \\ \alpha_{1} \cdot\left(X_{\text {rand }}^{t}+\beta \cdot\left|X_{\text {rand }}^{t}-\mathbf{X}_{i}^{t}\right|\right)+\alpha_{2} \cdot \mathbf{X}_{i-1}^{t}, & i=2,3, \cdots, N P \end{array}, \text { if rand }<\frac{t}{t_{\max }}\right. \\ \left\{\begin{array}{ll} \alpha_{1} \cdot\left(X_{\text {best }}^{t}+\beta \cdot\left|X_{\text {best }}^{t}-\mathbf{X}_{i}^{t}\right|\right)+\alpha_{2} \cdot \mathbf{X}_{i}^{t}, & i=1 \\ \alpha_{1} \cdot\left(X_{\text {best }}^{t}+\beta \cdot\left|X_{\text {best }}^{t}-\mathbf{X}_{i}^{t}\right|\right)+\alpha_{2} \cdot \mathbf{X}_{i-1}^{t}, & i=2,3, \cdots, N P \end{array}, \text { if rand } \geq \frac{t}{t_{\max }}\right. \end{array}\right. \tag{8}
Xit+1=⎩⎪⎪⎨⎪⎪⎧{α1⋅(Xrand t+β⋅∣Xrand t−Xit∣)+α2⋅Xit,α1⋅(Xrand t+β⋅∣Xrand t−Xit∣)+α2⋅Xi−1t,i=1i=2,3,⋯,NP, if rand <tmaxt{α1⋅(Xbest t+β⋅∣Xbest t−Xit∣)+α2⋅Xit,α1⋅(Xbest t+β⋅∣Xbest t−Xit∣)+α2⋅Xi−1t,i=1i=2,3,⋯,NP, if rand ≥tmaxt(8)
1.3 抛物线觅食
金枪鱼除了形成螺旋觅食外,还形成抛物线合作觅食。金枪鱼以食物为参照点形成抛物线形。此外,金枪鱼通过在周围搜索来寻找食物。假设两种方法的选择概率均为50%,则两种方法同时进行。具体的数学模型描述如下:
X
i
t
+
1
=
{
X
best
t
+
rand
⋅
(
X
best
t
−
X
i
t
)
+
T
F
⋅
p
2
⋅
(
X
best
t
−
X
i
t
)
,
if rand
<
0.5
T
F
⋅
p
2
⋅
X
i
t
,
if rand
≥
0.5
(9)
\mathbf{X}_{i}^{t+1}=\left\{\begin{array}{ll} \mathbf{X}_{\text {best }}^{t}+\operatorname{rand} \cdot\left(\mathbf{X}_{\text {best }}^{t}-\mathbf{X}_{i}^{t}\right)+T F \cdot p^{2} \cdot\left(\mathbf{X}_{\text {best }}^{t}-\mathbf{X}_{i}^{t}\right), & \text { if rand }<0.5 \\ T F \cdot p^{2} \cdot \mathbf{X}_{i}^{t}, & \text { if rand } \geq 0.5 \end{array}\right. \tag{9}
Xit+1={Xbest t+rand⋅(Xbest t−Xit)+TF⋅p2⋅(Xbest t−Xit),TF⋅p2⋅Xit, if rand <0.5 if rand ≥0.5(9)
p = ( 1 − t t max ) t / t max (10) p=\left(1-\frac{t}{t_{\max }}\right)^{t / t_{\max }} \tag{10} p=(1−tmaxt)t/tmax(10)
其中, T F TF TF是一个值为1或−1的随机数。
算法流程图如下:

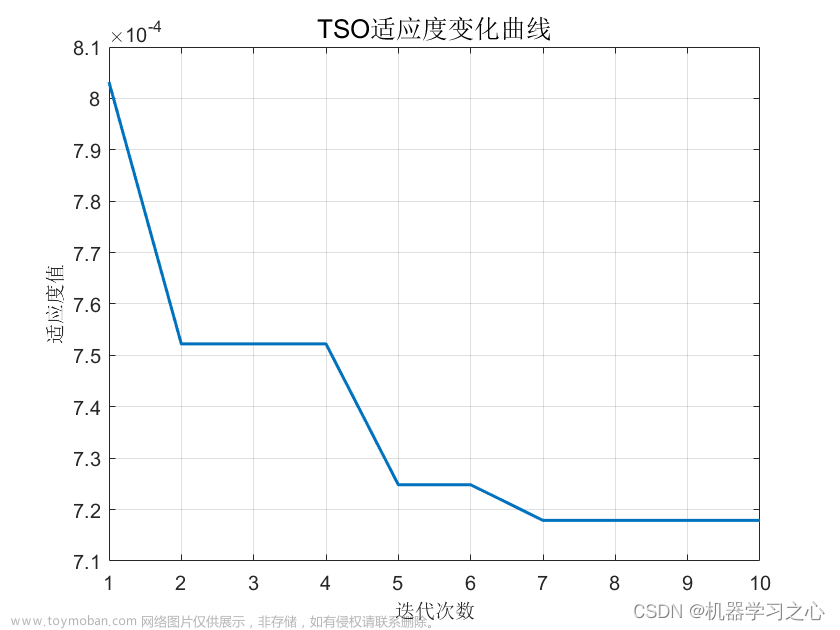
2.实验结果
 文章来源:https://www.toymoban.com/news/detail-425141.html
文章来源:https://www.toymoban.com/news/detail-425141.html
3.参考文献
[1] Lei Xie, Tong Han, Huan Zhou, et al. Tuna Swarm Optimization: A Novel Swarm-Based Metaheuristic Algorithm for Global Optimization[J]. Computational Intelligence and Neuroscience, vol. 2021, Article ID 9210050, 22 pages, 2021.文章来源地址https://www.toymoban.com/news/detail-425141.html
4.Matlab
到了这里,关于智能优化算法:金枪鱼群优化算法-附代码的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!