A*寻路算法-Toy模板网

这篇具有很好参考价值的文章主要介绍了A*寻路算法。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

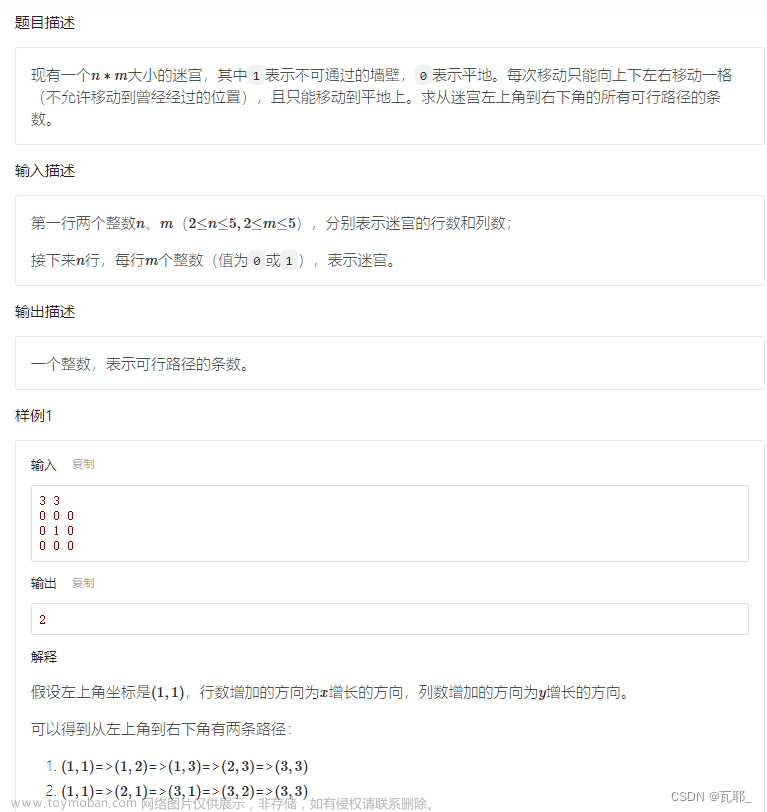
各寻路算法之间的比较

深度优先算法（BFS）在所有方向上平等的探索，是最好写的寻路算法

Dijkstra算法优先考虑低成本的路径，在游戏中可以规定远离敌人、避开森林需要更高的成本，所以当移动成本发生变化的时候我们使用该算法而不是BFS

A*寻路是对Dijkstra算法的修改，针对单个目标时进行了优化，Dijkstra的算法可以找到所有位置的路径;A 查找到一个位置的路径，或多个位置中最近的路径。它优先考虑似乎更接近目标的路径。

下图依次表示他们的搜索区间

A*寻路算法

Dijkstra的算法可以很好地找到最短的路径，但它浪费了时间探索那些没有希望的方向。Greedy Best-First在有希望的方向上探索，但它可能不会找到最短的路径。A* 算法同时使用从起点开始的实际距离和到目标的估计距离。

不同算法情况下不同的搜索范围和最终路线

A*寻路算法

A*寻路算法的过程

对于任意一个格子n，其估价函数如下：

f(n) = g(n) + h(n)

其中 g(n) 指的是从起始格子到格子n的实际代价，而 h(n) 指的是从格子n到终点格子的估计代价。

我们找到周围格子中f(n)值最小的各格子，在计算他周围格子的f(n)
一直找出边界格子中的f(n)最小的格子，直到找到与重点相邻的格子。

A*对启发式方法的使用

启发式算法，即优先搜索最有可能产生最佳路径的格子。

对于h（n）函数，不同的表示方法会导致最终结果的不同，比如如果采用曼哈顿距离（只能水平和垂直移动）和欧几里得距离（直线距离）

h(n)的具体影响为：

在一个极端，如果是0,那么会漫无目的的寻找，A*变成Dijkstra的算法，它保证找到一个最短的路径。
如果始终低于到目标实际距离，则保证 A* 找到最短路径。越低，节点 A* 扩展得越多，速度越慢。
如果正好等于到目标实际距离，则 A* 只会遵循最佳路径，从不扩展其他任何内容，使其非常快。虽然您无法在所有情况下都做到这一点，但在某些特殊情况下可以使其精确。很高兴知道，给定完美的信息，A *将表现完美。
如果大于到目标实际距离，则A *不能保证找到最短的路径，但它可以运行得更快。
在另一个极端，如果非常高，那么主要取决与h(n)，而A*变成了贪心算法

使用具体的移动方式匹配地图：

在允许 4 个方向移动的正方形网格上，使用曼哈顿距离 .
在允许 8 个方向移动的方形网格上，使用对角线距离 .

A*算法的具体实现

地图中允许8D运动，h（n）采用对角线加直线运动。我们就可以根据水平方向的差值与竖直方向的差值中较小的那个值，计算出对角线，然后再平移。

横向纵向的格子的单位消耗为10，对角单位消耗为14。

定义一个OpenList，用于存储和搜索当前最小值的格子。

定义一个CloseList，用于标记已经处理过的格子，以防止重复搜索。

将OpenList中f值最小的点作为当前点，加入邻居点到OpenList

对于邻居点执行以下代码伪代码：

如果邻居点在OpenList中
    计算当前值的G与该邻居点的G值
    如果G值比该邻居点的G值小
        将当前点设置为该邻居点的父节点
        更新该邻居点的GF值
若不在
    计算并设置当前点与该邻居点的G值
    计算并设置当前点与该邻居点的H值
    计算并设置该邻居点的F值
    将当前点设置为该邻居点的父节点

判断终点是否在OpenList中，如果已在OpenList中，则返回该点，其父节点连起来的路径就是A*搜索的路径。如果不在，则重复执行2，3，4，5。直到找到终点，或者OpenList中节点数量为0。

格子的记录值

public class Node
{
    Int2 m_position;//下标
    public Int2 position => m_position;
    public Node parent;//上一个node
    
    //角色到该节点的实际距离
    int m_g;
    public int g {
        get => m_g;
        set {
            m_g = value;
            m_f = m_g + m_h;
        }
    }

    //该节点到目的地的估价距离
    int m_h;
    public int h {
        get => m_h;
        set {
            m_h = value;
            m_f = m_g + m_h;
        }
    }

    int m_f;
    public int f => m_f;

    public Node(Int2 pos, Node parent, int g, int h) {
        m_position = pos;
        this.parent = parent;
        m_g = g;
        m_h = h;
        m_f = m_g + m_h;
    }
}

A*过程

public class AStar {
    static int FACTOR = 10;//水平竖直相邻格子的距离
    static int FACTOR_DIAGONAL = 14;//对角线相邻格子的距离

    bool m_isInit = false;
    public bool isInit => m_isInit;

    UIGridController[,] m_map;//地图数据
    Int2 m_mapSize;
    Int2 m_player, m_destination;//起始点和结束点坐标
    EvaluationFunctionType m_evaluationFunctionType;//估价方式

    Dictionary<Int2, Node> m_openDic = new Dictionary<Int2, Node>();//准备处理的网格
    Dictionary<Int2, Node> m_closeDic = new Dictionary<Int2, Node>();//完成处理的网格

    Node m_destinationNode;

    public void Init(UIGridController[,] map, Int2 mapSize, Int2 player, Int2 destination, EvaluationFunctionType type = EvaluationFunctionType.Diagonal) {
        m_map = map;
        m_mapSize = mapSize;
        m_player = player;
        m_destination = destination;
        m_evaluationFunctionType = type;

        m_openDic.Clear();
        m_closeDic.Clear();

        m_destinationNode = null;

        //将起始点加入open中
        AddNodeInOpenQueue(new Node(m_player, null, 0, 0));
        m_isInit = true;
    }

    //计算寻路
    public IEnumerator Start() {
        while(m_openDic.Count > 0 && m_destinationNode == null) {
            //按照f的值升序排列
            m_openDic = m_openDic.OrderBy(kv => kv.Value.f).ToDictionary(p => p.Key, o => o.Value);
            //提取排序后的第一个节点
            Node node = m_openDic.First().Value;
            //因为使用的不是Queue，因此要从open中手动删除该节点
            m_openDic.Remove(node.position);
            //处理该节点相邻的节点
            OperateNeighborNode(node);
            //处理完后将该节点加入close中
            AddNodeInCloseDic(node);
            yield return null;
        }
        if(m_destinationNode == null)
            Debug.LogError("找不到可用路径");
        else
            ShowPath(m_destinationNode);
    }

    //处理相邻的节点
    void OperateNeighborNode(Node node) {
        for(int i = -1; i < 2; i++) {
            for(int j = -1; j < 2; j++) {
                if(i == 0 && j == 0)
                    continue;
                Int2 pos = new Int2(node.position.x + i, node.position.y + j);
                //超出地图范围
                if(pos.x < 0 || pos.x >= m_mapSize.x || pos.y < 0 || pos.y >= m_mapSize.y)
                    continue;
                //已经处理过的节点
                if(m_closeDic.ContainsKey(pos))
                    continue;
                //障碍物节点
                if(m_map[pos.x, pos.y].state == GridState.Obstacle)
                    continue;
                //将相邻节点加入open中
                if(i == 0 || j == 0)
                    AddNeighborNodeInQueue(node, pos, FACTOR);
                else
                    AddNeighborNodeInQueue(node, pos, FACTOR_DIAGONAL);
            }
        }
    }

    //将节点加入到open中
    void AddNeighborNodeInQueue(Node parentNode, Int2 position, int g) {
        //当前节点的实际距离g等于上个节点的实际距离加上自己到上个节点的实际距离
        int nodeG = parentNode.g + g;
        //如果该位置的节点已经在open中
        if(m_openDic.ContainsKey(position)) {
            //比较实际距离g的值，用更小的值替换
            if(nodeG < m_openDic[position].g) {
                m_openDic[position].g = nodeG;
                m_openDic[position].parent = parentNode;
                ShowOrUpdateAStarHint(m_openDic[position]);
            }
        }
        else {
            //生成新的节点并加入到open中
            Node node = new Node(position, parentNode, nodeG, GetH(position));
            //如果周边有一个是终点，那么说明已经找到了。
            if(position == m_destination)
                m_destinationNode = node;
            else
                AddNodeInOpenQueue(node);
        }
    }

    //加入open中，并更新网格状态
    void AddNodeInOpenQueue(Node node) {
        m_openDic[node.position] = node;
        ShowOrUpdateAStarHint(node);
    }

    void ShowOrUpdateAStarHint(Node node) {
        m_map[node.position.x, node.position.y].ShowOrUpdateAStarHint(node.g, node.h, node.f,
            node.parent == null ? Vector2.zero : new Vector2(node.parent.position.x - node.position.x, node.parent.position.y - node.position.y));
    }

    //加入close中，并更新网格状态
    void AddNodeInCloseDic(Node node) {
        m_closeDic.Add(node.position, node);
        m_map[node.position.x, node.position.y].ChangeInOpenStateToInClose();
    }

    //寻路完成，显示路径
    void ShowPath(Node node) {
        while(node != null) {
            m_map[node.position.x, node.position.y].ChangeToPathState();
            node = node.parent;
        }
    }

    //获取估价距离
    int GetH(Int2 position) {
        if(m_evaluationFunctionType == EvaluationFunctionType.Manhattan)
            return GetManhattanDistance(position);
        else if(m_evaluationFunctionType == EvaluationFunctionType.Diagonal)
            return GetDiagonalDistance(position);
        else
            return Mathf.CeilToInt(GetEuclideanDistance(position));
    }

    //获取对角线距离
    int GetDiagonalDistance(Int2 position) {
        int x = Mathf.Abs(m_destination.x - position.x);
        int y = Mathf.Abs(m_destination.y - position.y);
        int min = Mathf.Min(x, y);
        return min * FACTOR_DIAGONAL + Mathf.Abs(x - y) * FACTOR;
    }

    //获取曼哈顿距离
    int GetManhattanDistance(Int2 position) {
        return Mathf.Abs(m_destination.x - position.x) * FACTOR + Mathf.Abs(m_destination.y - position.y) * FACTOR;
    }



    public void Clear() {
        foreach(var pos in m_openDic.Keys) {
            m_map[pos.x, pos.y].ClearAStarHint();
        }
        m_openDic.Clear();

        foreach(var pos in m_closeDic.Keys) {
            m_map[pos.x, pos.y].ClearAStarHint();
        }
        m_closeDic.Clear();
        m_destinationNode = null;
        m_isInit = false;
    }
}