目录
基本思想
实现
伪代码
实际问题求解
最小生成树:带权连通图的生成树中 边的权值之和最小的生成树。
- 最小生成树不是唯一的。当图中的各边权值互不相等时,最小生成树是唯一的;
- 若无向连通图本身是一棵树时(边数比顶点数少1 ),则最小生成树就是它本身。
- 最小生成树的边数为顶点数减1。
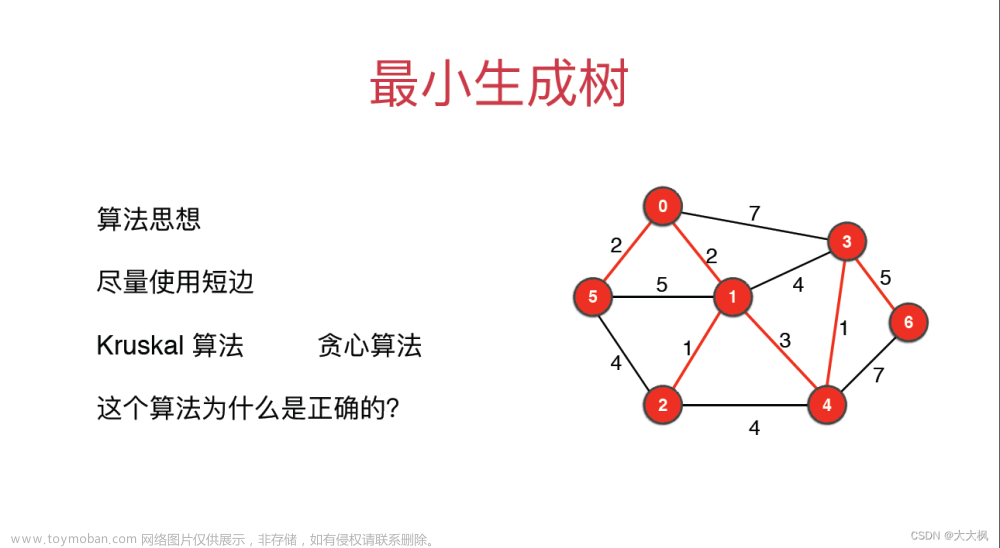
基本思想
(找权值最小的边)
- 初始时为只有n 个顶点而无边的非连通图 T 每个顶点自成一个连通分量,然后按照边的权值由小到大的顺序;
- 不断选取当前未被选取过且权值最小的边,若该边依附的顶点落在 T 中不同的连通分量上,则将此边加入 T , 否则舍弃此边而选择下一条权值最小的边。以此类推,直至T中所有顶点都在一个连通分量上。

- 通常在Kruskal算法中,采用堆来存放边的集合,因此每次选择最小权值的边只需的时间。此外,由于生成树中的所有边可视为一个等价类,因此每次添加新的边的过程类似于求解等价类的过程,由此可以采用并查集的数据结构来描述从而构造广的时间复杂度为。(|E|表示边数)
-
Kruskal算法适合于边稀疏而顶点较多的图。
实现
伪代码
void Kruskal(V,T) {
T=V; //初始化树,仅含顶点
numS=n; //连通分量数
while(numS>l){ //若连通分量数大于1
从E中取出权值最小的边(v,u);
if(v和 u 属于T 中不同的连通分量){
T=TU{ (v,u) };//将此边加入生成树中
numS-; //连通分量数减1
}
}
}实际问题求解
P1546 [USACO3.1]最短网络 Agri-Net
题目背景:Farmer John 被选为他们镇的镇长!他其中一个竞选承诺就是在镇上建立起互联网,并连接到所有的农场。当然,他需要你的帮助。
题目描述:FJ 已经给他的农场安排了一条高速的网络线路,他想把这条线路共享给其他农场。为了用最小的消费,他想铺设最短的光纤去连接所有的农场。
你将得到一份各农场之间连接费用的列表,你必须找出能连接所有农场并所用光纤最短的方案。每两个农场间的距离不会超过。文章来源:https://www.toymoban.com/news/detail-425408.html
(采用基本Kruskal算法求解:Prim算法求解见http://t.csdn.cn/OFNwt)文章来源地址https://www.toymoban.com/news/detail-425408.html
public class MST {
class Edge{
int x,y,wei;
public Edge(int x,int y,int wei){
this.x=x;
this.y=y;
this.wei=wei;
}
}
//并查集
class UFSets{
private int[] vex;
public UFSets(int n){
vex=new int[n];
for (int i = 0; i < n; i++) {
vex[i]=i;
}
}
//x的最高祖宗
public int find (int x){
return vex[x]==x?x:find(vex[x]);
}
//合并
public void union (int x,int y){
int fx=find(x);
int fy=find(y);
if (fx!=fy){
vex[fx]=fy;
}
}
}
public int kruskal(int[][] w){
int n=w.length;
//最小生成树总权值
int result=0;
//顶点集初始化
UFSets vex=new UFSets(n);
List<Edge> list=new ArrayList<>();
for (int i = 0; i < n; i++) {
for (int j = i; j < n; j++) {
if (w[i][j]>0){
list.add(new Edge(i,j,w[i][j]));
}
}
}
list.sort(new Comparator<Edge>() {
@Override
public int compare(Edge o1, Edge o2) {
return o1.wei-o2.wei;
}
});
//选n个边
for (Edge e : list) {
if (n<=0){
break;
}
//边的两个点属于不同连通分量,则加入这条边
if (vex.find(e.x)!=vex.find(e.y)){
vex.union(e.x,e.y);
result+=e.wei;
n--;
}
}
return result;
}
public static void main(String[] args) {
Scanner scan=new Scanner(System.in);
int n=scan.nextInt();
int[][] w=new int[n][n];
for (int i = 0; i < w.length; i++) {
for (int j = 0; j < w.length; j++) {
w[i][j]=scan.nextInt();
}
}
System.out.println(new MST().kruskal(w));
}
}到了这里,关于最小生成树——Kruskal算法的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!