[]{#_Toc405731550 .anchor}
目录
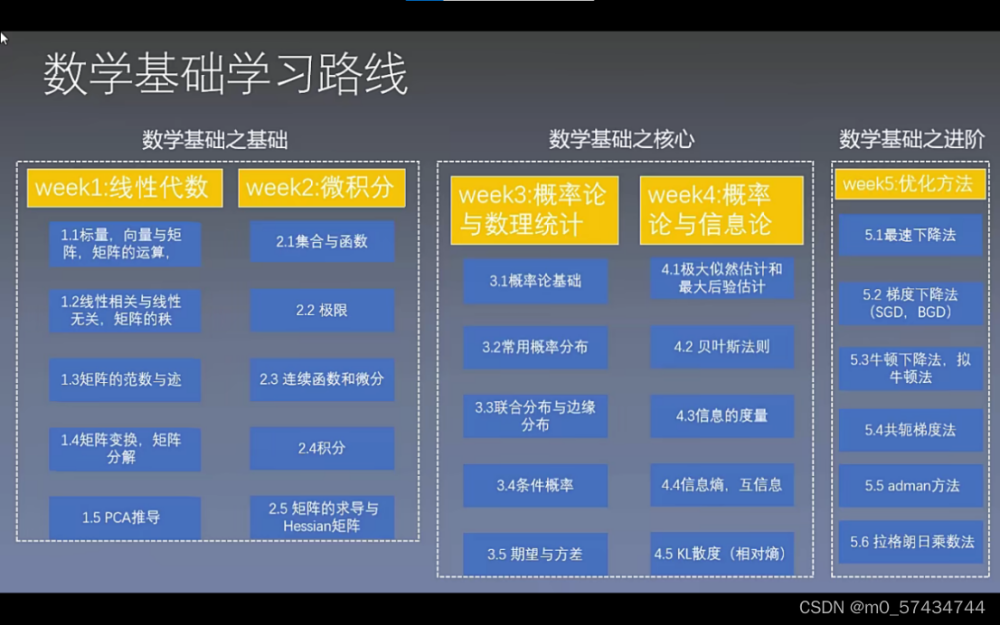
机器学习的数学基础 1
高等数学 1
线性代数 9
概率论和数理统计 19
机器学习的数学基础 {#机器学习的数学基础 .58}
高等数学
1.导数定义:
导数和微分的概念
f
′
(
x
0
)
=
lim
Δ
x
→
0
f
(
x
0
+
Δ
x
)
−
f
(
x
0
)
Δx
f'(x_{0}) = \lim_{\Delta x \rightarrow 0}\,\frac{f(x_{0} + \Delta x) - f(x_{0})}{\text{Δx}}
f′(x0)=limΔx→0Δxf(x0+Δx)−f(x0)
(1)
或者:
f
′
(
x
0
)
=
lim
x
→
x
0
f
(
x
)
−
f
(
x
0
)
x
−
x
0
f'(x_{0}) = \lim_{x \rightarrow x_{0}}\,\frac{f(x) - f(x_{0})}{x - x_{0}}
f′(x0)=limx→x0x−x0f(x)−f(x0)
(2)
2.左右导数导数的几何意义和物理意义
函数 f ( x ) f(x) f(x)在 x 0 x_{0} x0处的左、右导数分别定义为:
左导数: f ′ − ( x 0 ) = lim Δ x → 0 − f ( x 0 + Δ x ) − f ( x 0 ) Δx = lim x → x 0 − f ( x ) − f ( x 0 ) x − x 0 , ( x = x 0 + Δ x ) {f'}_{-}(x_{0}) = \lim_{\Delta x \rightarrow 0^{-}}\,\frac{f(x_{0} + \Delta x) - f(x_{0})}{\text{Δx}} = \lim_{x \rightarrow x_{0}^{-}}\,\frac{f(x) - f(x_{0})}{x - x_{0}},(x = x_{0} + \Delta x) f′−(x0)=limΔx→0−Δxf(x0+Δx)−f(x0)=limx→x0−x−x0f(x)−f(x0),(x=x0+Δx)
右导数: f ′ + ( x 0 ) = lim Δ x → 0 + f ( x 0 + Δ x ) − f ( x 0 ) Δx = lim x → x 0 + f ( x ) − f ( x 0 ) x − x 0 {f'}_{+}(x_{0}) = \lim_{\Delta x \rightarrow 0^{+}}\,\frac{f(x_{0} + \Delta x) - f(x_{0})}{\text{Δx}} = \lim_{x \rightarrow x_{0}^{+}}\,\frac{f(x) - f(x_{0})}{x - x_{0}} f′+(x0)=limΔx→0+Δxf(x0+Δx)−f(x0)=limx→x0+x−x0f(x)−f(x0)
3.函数的可导性与连续性之间的关系
Th1:
函数
f
(
x
)
f(x)
f(x)在
x
0
x_{0}
x0处可微
⇔
f
(
x
)
\Leftrightarrow f(x)
⇔f(x)在
x
0
x_{0}
x0处可导。
**Th2:**若函数在点 x 0 x_{0} x0处可导,则 y = f ( x ) y = f(x) y=f(x)在点 x 0 x_{0} x0处连续,反之则不成立.即函数连续不一定可导。
Th3: f ′ ( x 0 ) f'(x_{0}) f′(x0)存在 ⇔ f ′ − ( x 0 ) = f ′ + ( x 0 ) \Leftrightarrow {f'}_{-}(x_{0}) = {f'}_{+}(x_{0}) ⇔f′−(x0)=f′+(x0)
4.平面曲线的切线和法线
切线方程 : y − y 0 = f ′ ( x 0 ) ( x − x 0 ) y - y_{0} = f'(x_{0})(x - x_{0}) y−y0=f′(x0)(x−x0)
法线方程: y − y 0 = − 1 f ′ ( x 0 ) ( x − x 0 ) , f ′ ( x 0 ) ≠ 0 y - y_{0} = - \frac{1}{f'(x_{0})}(x - x_{0}),f'(x_{0}) \neq 0 y−y0=−f′(x0)1(x−x0),f′(x0)=0
5.四则运算法则
设函数 u = u ( x ) , v = v ( x ) u = u(x),v = v(x) u=u(x),v=v(x)在点 x x x可导,则:
(1) ( u ± v ) ′ = u ′ ± v ′ \left( u \pm v \right)^{'} = u^{'} \pm v^{'} (u±v)′=u′±v′ \text{\ \ \ \ }
(2)
(
uv
)
′
=
uv
′
+
vu
′
(\text{uv})' = \text{uv}' + \text{vu}'
(uv)′=uv′+vu′
d
(
uv
)
=
udv
+
vdu
d(\text{uv}) = \text{udv} + \text{vdu}
d(uv)=udv+vdu
(3)
(
u
v
)
′
=
vu
′
−
uv
′
v
2
(
v
≠
0
)
(\frac{u}{v})' = \frac{\text{vu}' - \text{uv}'}{v^{2}}(v \neq 0)
(vu)′=v2vu′−uv′(v=0)
d
(
u
v
)
=
vdu
−
udv
v
2
d(\frac{u}{v}) = \frac{\text{vdu} - \text{udv}}{v^{2}}
d(vu)=v2vdu−udv
6.基本导数与微分表
(1) y = c y = c y=c(常数) 则: y ′ = 0 y^{'} = 0 y′=0 dy = 0 \text{dy} = 0 dy=0
(2)
y
=
x
α
y = x^{\alpha}
y=xα(
α
\alpha
α为实数) 则:
y
′
=
α
x
α
−
1
y' = \alpha x^{\alpha - 1}
y′=αxα−1
dy
=
α
x
α
−
1
dx
\text{dy} = \alpha x^{\alpha - 1}\text{dx}
dy=αxα−1dx
(3)
y
=
a
x
y = a^{x}
y=ax 则:
y
′
=
a
x
ln
a
y' = a^{x}\ln a
y′=axlna
dy
=
a
x
ln
adx
\text{dy} = a^{x}\ln\text{adx}
dy=axlnadx
特例:
(
e
x
)
′
=
e
x
(e^{x})' = e^{x}
(ex)′=ex
d
(
e
x
)
=
e
x
dx
d(e^{x}) = e^{x}\text{dx}
d(ex)=exdx
(4)
y
′
=
1
x
ln
a
y' = \frac{1}{x\ln a}
y′=xlna1 则:
dy
=
1
x
ln
a
dx
\text{dy} = \frac{1}{x\ln a}\text{dx}
dy=xlna1dx
特例:
y
=
l
n
x
y = lnx
y=lnx
(
l
n
x
)
′
=
1
x
(lnx)' = \frac{1}{x}
(lnx)′=x1
d
(
l
n
x
)
=
1
x
dx
d(lnx) = \frac{1}{x}\text{dx}
d(lnx)=x1dx
(5) y = s i n x y = sinx y=sinx 则: y ′ = c o s x y' = cosx y′=cosx d ( s i n x ) = c o s xdx d(sinx) = cos\text{xdx} d(sinx)=cosxdx
(6) y = c o s x y = cosx y=cosx 则: y ′ = − s i n x y' = - sinx y′=−sinx d ( c o s x ) = − s i n xdx d(cosx) = - sin\text{xdx} d(cosx)=−sinxdx
(7)
y
=
t
a
n
x
y = tanx
y=tanx 则:
y
′
=
1
cos
2
x
=
sec
2
x
y^{'} = \frac{1}{\cos^{2}x} = \sec^{2}x
y′=cos2x1=sec2x
d
(
t
a
n
x
)
=
sec
2
xdx
d(tanx) = \sec^{2}\text{xdx}
d(tanx)=sec2xdx
(8)
y
=
c
o
t
x
y = cotx
y=cotx 则:
y
′
=
−
1
sin
2
x
=
−
csc
2
x
y' = - \frac{1}{\sin^{2}x} = - \csc^{2}x
y′=−sin2x1=−csc2x
d
(
c
o
t
x
)
=
−
csc
2
xdx
d(cotx) = - \csc^{2}\text{xdx}
d(cotx)=−csc2xdx
(9) y = s e c x y = secx y=secx 则: y ′ = s e c x tan x y' = secx\tan x y′=secxtanx d ( s e c x ) = s e c x tan xdx d(secx) = secx\tan\text{xdx} d(secx)=secxtanxdx
(10) y = c s c x y = cscx y=cscx 则: y ′ = − c s c x cot x y' = - cscx\cot x y′=−cscxcotx d ( c s c x ) = − c s c x cot xdx d(cscx) = - cscx\cot\text{xdx} d(cscx)=−cscxcotxdx
(11)
y
=
a
r
c
s
i
n
x
y = arcsinx
y=arcsinx 则:
y
′
=
1
1
−
x
2
y' = \frac{1}{\sqrt{1 - x^{2}}}
y′=1−x21
d
(
a
r
c
s
i
n
x
)
=
1
1
−
x
2
dx
d(arcsinx) = \frac{1}{\sqrt{1 - x^{2}}}\text{dx}
d(arcsinx)=1−x21dx
(12)
y
=
a
r
c
c
o
s
x
y = arccosx
y=arccosx 则:
y
′
=
−
1
1
−
x
2
y' = - \frac{1}{\sqrt{1 - x^{2}}}
y′=−1−x21
d
(
a
r
c
c
o
s
x
)
=
−
1
1
−
x
2
dx
d(arccosx) = - \frac{1}{\sqrt{1 - x^{2}}}\text{dx}
d(arccosx)=−1−x21dx
(13)
y
=
a
r
c
t
a
n
x
y = arctanx
y=arctanx 则:
y
′
=
1
1
+
x
2
y' = \frac{1}{1 + x^{2}}
y′=1+x21
d
(
a
r
c
t
a
n
x
)
=
1
1
+
x
2
dx
d(arctanx) = \frac{1}{1 + x^{2}}\text{dx}
d(arctanx)=1+x21dx
(14)
y
=
a
r
c
c
o
t
x
y = arccotx
y=arccotx 则:
y
′
=
−
1
1
+
x
2
y' = - \frac{1}{1 + x^{2}}
y′=−1+x21
d
(
a
r
c
c
o
t
x
)
=
−
1
1
+
x
2
dx
d(arccotx) = - \frac{1}{1 + x^{2}}\text{dx}
d(arccotx)=−1+x21dx
(15) y = s x y = sx y=sx 则: y ′ = c x y' = cx y′=cx d ( s x ) = c x d x d(sx) = cxdx d(sx)=cxdx
(16) y = c x y = cx y=cx 则: y ′ = s x y' = sx y′=sx d ( c x ) = s x d x d(cx) = sxdx d(cx)=sxdx
7.复合函数,反函数,隐函数以及参数方程所确定的函数的微分法
(1) 反函数的运算法则:
设
y
=
f
(
x
)
y = f(x)
y=f(x)在点
x
x
x的某邻域内单调连续,在点
x
x
x处可导且
f
′
(
x
)
≠
0
f'(x) \neq 0
f′(x)=0,则其反函数在点
x
x
x所对应的
y
y
y处可导,并且有
dy
dx
=
1
dx
dy
\frac{\text{dy}}{\text{dx}} = \frac{1}{\frac{\text{dx}}{\text{dy}}}
dxdy=dydx1
(2)
复合函数的运算法则:若
μ
=
φ
(
x
)
\mu = \varphi(x)
μ=φ(x)在点
x
x
x可导,而
y
=
f
(
μ
)
y = f(\mu)
y=f(μ)在对应点
μ
\mu
μ(
μ
=
φ
(
x
)
\mu = \varphi(x)
μ=φ(x))可导,则复合函数
y
=
f
(
φ
(
x
)
)
y = f(\varphi(x))
y=f(φ(x))在点
x
x
x可导,且
y
′
=
f
′
(
μ
)
⋅
φ
′
(
x
)
y' = f'(\mu) \cdot \varphi'(x)
y′=f′(μ)⋅φ′(x)
(3) 隐函数导数 dy dx \frac{\text{dy}}{\text{dx}} dxdy的求法一般有三种方法:
1)方程两边对
x
x
x求导,要记住
y
y
y是
x
x
x的函数,则
y
y
y的函数是
x
x
x的复合函数.例如
1
y
\frac{1}{y}
y1,
y
2
y^{2}
y2,
lny
\text{lny}
lny,
e
y
e^{y}
ey等均是
x
x
x的复合函数.
对
x
x
x求导应按复合函数连锁法则做。
2)公式法.由
F
(
x
,
y
)
=
0
F(x,y) = 0
F(x,y)=0知
dy
dx
=
−
F
′
x
(
x
,
y
)
F
′
y
(
x
,
y
)
\frac{\text{dy}}{\text{dx}} = - \frac{{F'}_{x}(x,y)}{{F'}_{y}(x,y)}
dxdy=−F′y(x,y)F′x(x,y),其中,
F
′
x
(
x
,
y
)
{F'}_{x}(x,y)
F′x(x,y),
F
′
y
(
x
,
y
)
{F'}_{y}(x,y)
F′y(x,y)分别表示
F
(
x
,
y
)
F(x,y)
F(x,y)对
x
x
x和
y
y
y的偏导数。
3)利用微分形式不变性
8.常用高阶导数公式
(1)KaTeX parse error: Got group of unknown type: 'internal'
(2)KaTeX parse error: Got group of unknown type: 'internal'
(3)KaTeX parse error: Got group of unknown type: 'internal'
(4)KaTeX parse error: Got group of unknown type: 'internal'
(5)KaTeX parse error: Got group of unknown type: 'internal'
(6)莱布尼兹公式:若
u
(
x
)
,
v
(
x
)
u(x)\,,v(x)
u(x),v(x)均
n
n
n阶可导,则:
(
uv
)
(
n
)
=
∑
i
=
0
n
c
n
i
u
(
i
)
v
(
n
−
i
)
{(\text{uv})}^{(n)} = \sum_{i = 0}^{n}{c_{n}^{i}u^{(i)}v^{(n - i)}}
(uv)(n)=∑i=0ncniu(i)v(n−i),其中
u
(
0
)
=
u
u^{(0)} = u
u(0)=u,
v
(
0
)
=
v
v^{(0)} = v
v(0)=v
9.微分中值定理,泰勒公式
Th1:(费马定理)
若函数 f ( x ) f(x) f(x)满足条件:
(1)函数
f
(
x
)
f(x)
f(x)在
x
0
x_{0}
x0的某邻域内有定义,并且在此邻域内恒有
f
(
x
)
≤
f
(
x
0
)
f(x) \leq f(x_{0})
f(x)≤f(x0)或
f
(
x
)
≥
f
(
x
0
)
f(x) \geq f(x_{0})
f(x)≥f(x0),
(2) f ( x ) f(x) f(x)在 x 0 x_{0} x0处可导,则有 f ′ ( x 0 ) = 0 f'(x_{0}) = 0 f′(x0)=0
Th2:(罗尔定理)
设函数 f ( x ) f(x) f(x)满足条件:
(1)在闭区间
[
a
,
b
]
\lbrack a,b\rbrack
[a,b]上连续;
(2)在
(
a
,
b
)
(a,b)
(a,b)内可导;(3)
f
(
a
)
=
f
(
b
)
f\left( a \right) = f\left( b \right)
f(a)=f(b)
则在 ( a , b ) (a,b) (a,b)内 ∃ \exists ∃一个 ξ \xi ξ,使 f ′ ( ξ ) = 0 f'(\xi) = 0 f′(ξ)=0
Th3: (拉格朗日中值定理)
设函数 f ( x ) f(x) f(x)满足条件:
(1)在 [ a , b ] \lbrack a,b\rbrack [a,b]上连续;(2)在 ( a , b ) (a,b) (a,b)内可导;
则在 ( a , b ) (a,b) (a,b)内存在一个 ξ \xi ξ,使 f ( b ) − f ( a ) b − a = f ′ ( ξ ) \frac{f(b) - f(a)}{b - a} = f'(\xi) b−af(b)−f(a)=f′(ξ)
Th4: (柯西中值定理)
设函数 f ( x ) f(x) f(x), g ( x ) g(x) g(x)满足条件:
(1) 在
[
a
,
b
]
\lbrack a,b\rbrack
[a,b]上连续;(2)
在
(
a
,
b
)
(a,b)
(a,b)内可导且
f
′
(
x
)
f'(x)
f′(x),
g
′
(
x
)
g'(x)
g′(x)均存在,且
g
′
(
x
)
≠
0
g'(x) \neq 0
g′(x)=0
则在
(
a
,
b
)
(a,b)
(a,b)内存在一个
ξ
\xi
ξ,使
f
(
b
)
−
f
(
a
)
g
(
b
)
−
g
(
a
)
=
f
′
(
ξ
)
g
′
(
ξ
)
\frac{f(b) - f(a)}{g(b) - g(a)} = \frac{f'(\xi)}{g'(\xi)}
g(b)−g(a)f(b)−f(a)=g′(ξ)f′(ξ)
10.洛必达法则
法则Ⅰ( 0 0 \frac{\mathbf{0}}{\mathbf{0}} 00型不定式极限)
设函数
f
(
x
)
,
g
(
x
)
f\left( x \right),g\left( x \right)
f(x),g(x)满足条件:
lim
x
→
x
0
f
(
x
)
=
0
,
lim
x
→
x
0
g
(
x
)
=
0
\lim_{x \rightarrow x_{0}}\, f\left( x \right) = 0,\lim_{x \rightarrow x_{0}}\, g\left( x \right) = 0
limx→x0f(x)=0,limx→x0g(x)=0;
f
(
x
)
,
g
(
x
)
f\left( x \right),g\left( x \right)
f(x),g(x)在
x
0
x_{0}
x0的邻域内可导
(在
x
0
x_{0}
x0处可除外)且
g
′
(
x
)
≠
0
g'\left( x \right) \neq 0
g′(x)=0;
lim x → x 0 f ′ ( x ) g ′ ( x ) \lim_{x \rightarrow x_{0}}\,\frac{f'\left( x \right)}{g'\left( x \right)} limx→x0g′(x)f′(x)存在(或 ∞ \infty ∞)。
则:
lim
x
→
x
0
f
(
x
)
g
(
x
)
=
lim
x
→
x
0
f
′
(
x
)
g
′
(
x
)
\lim_{x \rightarrow x_{0}}\,\frac{f\left( x \right)}{g\left( x \right)} = \lim_{x \rightarrow x_{0}}\,\frac{f'\left( x \right)}{g'\left( x \right)}
limx→x0g(x)f(x)=limx→x0g′(x)f′(x)
法则
I
′
\mathbf{I'}
I′
(
0
0
\frac{\mathbf{0}}{\mathbf{0}}
00型不定式极限)
设函数
f
(
x
)
,
g
(
x
)
f\left( x \right),g\left( x \right)
f(x),g(x)满足条件:
lim
x
→
∞
f
(
x
)
=
0
,
lim
x
→
∞
g
(
x
)
=
0
\lim_{x \rightarrow \infty}\, f\left( x \right) = 0,\lim_{x \rightarrow \infty}\, g\left( x \right) = 0
limx→∞f(x)=0,limx→∞g(x)=0;存在一个
X
>
0
X > 0
X>0,当
∣
x
∣
>
X
\left| x \right| > X
∣x∣>X时,
f
(
x
)
,
g
(
x
)
f\left( x \right),g\left( x \right)
f(x),g(x)可导,且
g
′
(
x
)
≠
0
g'\left( x \right) \neq 0
g′(x)=0;
lim
x
→
x
0
f
′
(
x
)
g
′
(
x
)
\lim_{x \rightarrow x_{0}}\,\frac{f'\left( x \right)}{g'\left( x \right)}
limx→x0g′(x)f′(x)存在(或
∞
\infty
∞)。
则:
lim
x
→
x
0
f
(
x
)
g
(
x
)
=
lim
x
→
x
0
f
′
(
x
)
g
′
(
x
)
.
\lim_{x \rightarrow x_{0}}\,\frac{f\left( x \right)}{g\left( x \right)} = \lim_{x \rightarrow x_{0}}\,\frac{f'\left( x \right)}{g'\left( x \right)}.
limx→x0g(x)f(x)=limx→x0g′(x)f′(x).
法则Ⅱ( ∞ ∞ \frac{\mathbf{\infty}}{\mathbf{\infty}} ∞∞**型不定式极限) **
设函数
f
(
x
)
,
g
(
x
)
f\left( x \right),g\left( x \right)
f(x),g(x)满足条件:
lim
x
→
x
0
f
(
x
)
=
∞
,
lim
x
→
x
0
g
(
x
)
=
∞
\lim_{x \rightarrow x_{0}}\, f\left( x \right) = \infty,\lim_{x \rightarrow x_{0}}\, g\left( x \right) = \infty
limx→x0f(x)=∞,limx→x0g(x)=∞;
f
(
x
)
,
g
(
x
)
f\left( x \right),g\left( x \right)
f(x),g(x)在
x
0
x_{0}
x0 的邻域内可
导(在
x
0
x_{0}
x0处可除外)且
g
′
(
x
)
≠
0
g'\left( x \right) \neq 0
g′(x)=0;
lim
x
→
x
0
f
′
(
x
)
g
′
(
x
)
\lim_{x \rightarrow x_{0}}\,\frac{f'\left( x \right)}{g'\left( x \right)}
limx→x0g′(x)f′(x)存在(或
∞
\infty
∞)。
则:
lim
x
→
x
0
f
(
x
)
g
(
x
)
=
lim
x
→
x
0
f
′
(
x
)
g
′
(
x
)
.
\lim_{x \rightarrow x_{0}}\,\frac{f\left( x \right)}{g\left( x \right)} = \lim_{x \rightarrow x_{0}}\,\frac{f'\left( x \right)}{g'\left( x \right)}.
limx→x0g(x)f(x)=limx→x0g′(x)f′(x).
同理法则 I I ′ II' II′( ∞ ∞ \frac{\infty}{\infty} ∞∞型不定式极限)仿法则 I ′ I' I′可写出
11.泰勒公式
设函数 f ( x ) f(x) f(x)在点 x 0 x_{0} x0处的某邻域内具有 n + 1 n + 1 n+1阶导数,则对该邻域内异于 x 0 x_{0} x0的任意点 x x x,在 x 0 x_{0} x0与 x x x之间至少存在一个 ξ \xi ξ,使得:
f
(
x
)
=
f
(
x
0
)
+
f
′
(
x
0
)
(
x
−
x
0
)
+
1
2
!
f
′
′
(
x
0
)
(
x
−
x
0
)
2
+
⋯
f(x) = f(x_{0}) + f'(x_{0})(x - x_{0}) + \frac{1}{2!}f''(x_{0}){(x - x_{0})}^{2} + \cdots
f(x)=f(x0)+f′(x0)(x−x0)+2!1f′′(x0)(x−x0)2+⋯
+
f
(
n
)
(
x
0
)
n
!
(
x
−
x
0
)
n
+
R
n
(
x
)
+ \frac{f^{(n)}(x_{0})}{n!}{(x - x_{0})}^{n} + R_{n}(x)
+n!f(n)(x0)(x−x0)n+Rn(x)
其中
R
n
(
x
)
=
f
(
n
+
1
)
(
ξ
)
(
n
+
1
)
!
(
x
−
x
0
)
n
+
1
R_{n}(x) = \frac{f^{(n + 1)}(\xi)}{(n + 1)!}{(x - x_{0})}^{n + 1}
Rn(x)=(n+1)!f(n+1)(ξ)(x−x0)n+1称为
f
(
x
)
f(x)
f(x)在点
x
0
x_{0}
x0处的
n
n
n阶泰勒余项。
令 x 0 = 0 x_{0} = 0 x0=0,则 n n n阶泰勒公式:
f ( x ) = f ( 0 ) + f ′ ( 0 ) x + 1 2 ! f ′ ′ ( 0 ) x 2 + ⋯ + f ( n ) ( 0 ) n ! x n + R n ( x ) f(x) = f(0) + f'(0)x + \frac{1}{2!}f''(0)x^{2} + \cdots + \frac{f^{(n)}(0)}{n!}x^{n} + R_{n}(x) f(x)=f(0)+f′(0)x+2!1f′′(0)x2+⋯+n!f(n)(0)xn+Rn(x)……
(1) 其中
R
n
(
x
)
=
f
(
n
+
1
)
(
ξ
)
(
n
+
1
)
!
x
n
+
1
R_{n}(x) = \frac{f^{(n + 1)}(\xi)}{(n + 1)!}x^{n + 1}
Rn(x)=(n+1)!f(n+1)(ξ)xn+1,
ξ
\xi
ξ在0与
x
x
x之间。(1)式称为麦克劳林公式
常用五种函数在 x 0 = 0 x_{0} = 0 x0=0处的泰勒公式 :
e
x
=
1
+
x
+
1
2
!
x
2
+
⋯
+
1
n
!
x
n
+
x
n
+
1
(
n
+
1
)
!
e
ξ
e^{x} = 1 + x + \frac{1}{2!}x^{2} + \cdots + \frac{1}{n!}x^{n} + \frac{x^{n + 1}}{(n + 1)!}e^{\xi}
ex=1+x+2!1x2+⋯+n!1xn+(n+1)!xn+1eξ
或
=
1
+
x
+
1
2
!
x
2
+
⋯
+
1
n
!
x
n
+
o
(
x
n
)
= 1 + x + \frac{1}{2!}x^{2} + \cdots + \frac{1}{n!}x^{n} + o(x^{n})
=1+x+2!1x2+⋯+n!1xn+o(xn)
sin x = x − 1 3 ! x 3 + ⋯ + x n n ! sin nπ 2 + x n + 1 ( n + 1 ) ! sin ( ξ + n + 1 2 π ) \sin x = x - \frac{1}{3!}x^{3} + \cdots + \frac{x^{n}}{n!}\sin\frac{\text{nπ}}{2} + \frac{x^{n + 1}}{\left( n + 1 \right)!}\sin\left( \xi + \frac{n + 1}{2}\pi \right) sinx=x−3!1x3+⋯+n!xnsin2nπ+(n+1)!xn+1sin(ξ+2n+1π)
或
=
x
−
1
3
!
x
3
+
⋯
+
x
n
n
!
sin
nπ
2
+
o
(
x
n
)
= x - \frac{1}{3!}x^{3} + \cdots + \frac{x^{n}}{n!}\sin\frac{\text{nπ}}{2} + o\left( x^{n} \right)
=x−3!1x3+⋯+n!xnsin2nπ+o(xn)
cos x = 1 − 1 2 ! x 2 + ⋯ + x n n ! cos nπ 2 + x n + 1 ( n + 1 ) ! c o s ( ξ + n + 1 2 π ) \cos x = 1 - \frac{1}{2!}x^{2} + \cdots + \frac{x^{n}}{n!}\cos\frac{\text{nπ}}{2} + \frac{x^{n + 1}}{(n + 1)!}cos(\xi + \frac{n + 1}{2}\pi) cosx=1−2!1x2+⋯+n!xncos2nπ+(n+1)!xn+1cos(ξ+2n+1π)
或
=
1
−
1
2
!
x
2
+
⋯
+
x
n
n
!
cos
nπ
2
+
o
(
x
n
)
= 1 - \frac{1}{2!}x^{2} + \cdots + \frac{x^{n}}{n!}\cos\frac{\text{nπ}}{2} + o(x^{n})
=1−2!1x2+⋯+n!xncos2nπ+o(xn)
l n ( 1 + x ) = x − 1 2 x 2 + 1 3 x 3 − ⋯ + ( − 1 ) n − 1 x n n + ( − 1 ) n x n + 1 ( n + 1 ) ( 1 + ξ ) n + 1 ln(1 + x) = x - \frac{1}{2}x^{2} + \frac{1}{3}x^{3} - \cdots + {( - 1)}^{n - 1}\frac{x^{n}}{n} + \frac{{( - 1)}^{n}x^{n + 1}}{(n + 1){(1 + \xi)}^{n + 1}} ln(1+x)=x−21x2+31x3−⋯+(−1)n−1nxn+(n+1)(1+ξ)n+1(−1)nxn+1
或
=
x
−
1
2
x
2
+
1
3
x
3
−
⋯
+
(
−
1
)
n
−
1
x
n
n
+
o
(
x
n
)
= x - \frac{1}{2}x^{2} + \frac{1}{3}x^{3} - \cdots + {( - 1)}^{n - 1}\frac{x^{n}}{n} + o(x^{n})
=x−21x2+31x3−⋯+(−1)n−1nxn+o(xn)
(
1
+
x
)
m
=
1
+
mx
+
m
(
m
−
1
)
2
!
x
2
+
⋯
+
m
(
m
−
1
)
⋯
(
m
−
n
+
1
)
n
!
x
n
{(1 + x)}^{m} = 1 + \text{mx} + \frac{m(m - 1)}{2!}x^{2} + \cdots + \frac{m(m - 1)\cdots(m - n + 1)}{n!}x^{n}
(1+x)m=1+mx+2!m(m−1)x2+⋯+n!m(m−1)⋯(m−n+1)xn
+
m
(
m
−
1
)
⋯
(
m
−
n
+
1
)
(
n
+
1
)
!
x
n
+
1
(
1
+
ξ
)
m
−
n
−
1
+ \frac{m(m - 1)\cdots(m - n + 1)}{(n + 1)!}x^{n + 1}{(1 + \xi)}^{m - n - 1}
+(n+1)!m(m−1)⋯(m−n+1)xn+1(1+ξ)m−n−1
或
(
1
+
x
)
m
=
1
+
mx
+
m
(
m
−
1
)
2
!
x
2
+
⋯
+
m
(
m
−
1
)
⋯
(
m
−
n
+
1
)
n
!
x
n
+
o
(
x
n
)
{(1 + x)}^{m} = 1 + \text{mx} + \frac{m(m - 1)}{2!}x^{2} + \cdots + \frac{m(m - 1)\cdots(m - n + 1)}{n!}x^{n} + o(x^{n})
(1+x)m=1+mx+2!m(m−1)x2+⋯+n!m(m−1)⋯(m−n+1)xn+o(xn)
12.函数单调性的判断
Th1:
设函数
f
(
x
)
f(x)
f(x)在
(
a
,
b
)
(a,b)
(a,b)区间内可导,如果对
∀
x
∈
(
a
,
b
)
\forall x \in (a,b)
∀x∈(a,b),都有KaTeX parse error: Got group of unknown type: 'internal'(或KaTeX parse error: Got group of unknown type: 'internal'),则函数
f
(
x
)
f(x)
f(x)在
(
a
,
b
)
(a,b)
(a,b)内是单调增加的(或单调减少)。
Th2:
(取极值的必要条件)设函数
f
(
x
)
f(x)
f(x)在
x
0
x_{0}
x0处可导,且在
x
0
x_{0}
x0处取极值,则KaTeX parse error: Got group of unknown type: 'internal'.
Th3:
(取极值的第一充分条件)设函数
f
(
x
)
f(x)
f(x)在
x
0
x_{0}
x0的某一邻域内可微,且KaTeX parse error: Got group of unknown type: 'internal'(或
f
(
x
)
f(x)
f(x)在
x
0
x_{0}
x0处连续,但KaTeX parse error: Got group of unknown type: 'internal'不存在.)。
(1)若当 x x x经过 x 0 x_{0} x0时,KaTeX parse error: Got group of unknown type: 'internal'由“+”变“-”,则 f ( x 0 ) f(x_{0}) f(x0)为极大值;
(2)若当 x x x经过 x 0 x_{0} x0时,KaTeX parse error: Got group of unknown type: 'internal'由“-”变“+”,则 f ( x 0 ) f(x_{0}) f(x0)为极小值;
(3)若KaTeX parse error: Got group of unknown type: 'internal'经过 x = x 0 x = x_{0} x=x0的两侧不变号,则 f ( x 0 ) f(x_{0}) f(x0)不是极值。
Th4:
(取极值的第二充分条件)设
f
(
x
)
f(x)
f(x)在点
x
0
x_{0}
x0处有
f
′
′
(
x
)
≠
0
f''(x) \neq 0
f′′(x)=0,且KaTeX parse error: Got group of unknown type: 'internal',则:
当KaTeX parse error: Got group of unknown type: 'internal'时,
f
(
x
0
)
f(x_{0})
f(x0)为极大值;
当KaTeX parse error: Got group of unknown type: 'internal'时,
f
(
x
0
)
f(x_{0})
f(x0)为极小值.
注:如果KaTeX parse error: Got group of unknown type: 'internal',此方法失效。
13.渐近线的求法
(1)水平渐近线
若
lim
x
→
+
∞
f
(
x
)
=
b
\lim_{x \rightarrow + \infty}\, f(x) = b
limx→+∞f(x)=b,或
lim
x
→
−
∞
f
(
x
)
=
b
\lim_{x \rightarrow - \infty}\, f(x) = b
limx→−∞f(x)=b,则
y
=
b
y = b
y=b
称为函数
y
=
f
(
x
)
y = f(x)
y=f(x)的水平渐近线。
(2)铅直渐近线
若
lim
x
→
x
0
−
f
(
x
)
=
∞
\lim_{x \rightarrow x_{0}^{-}}\, f(x) = \infty
limx→x0−f(x)=∞,或
lim
x
→
x
0
+
f
(
x
)
=
∞
\lim_{x \rightarrow x_{0}^{+}}\, f(x) = \infty
limx→x0+f(x)=∞,则
x
=
x
0
x = x_{0}
x=x0
称为
y
=
f
(
x
)
y = f(x)
y=f(x)的铅直渐近线。
(3)斜渐近线
若
a
=
lim
x
→
∞
f
(
x
)
x
,
b
=
lim
x
→
∞
[
f
(
x
)
−
ax
]
a = \lim_{x \rightarrow \infty}\,\frac{f(x)}{x},\quad b = \lim_{x \rightarrow \infty}\,\lbrack f(x) - \text{ax}\rbrack
a=limx→∞xf(x),b=limx→∞[f(x)−ax],则
y
=
ax
+
b
y = \text{ax} + b
y=ax+b称为
y
=
f
(
x
)
y = f(x)
y=f(x)的斜渐近线。
14.函数凹凸性的判断
Th1: (凹凸性的判别定理)若在I上
f
′
′
(
x
)
<
0
f''(x) < 0
f′′(x)<0(或
f
′
′
(
x
)
>
0
f''(x) > 0
f′′(x)>0),
则
f
(
x
)
f(x)
f(x)在I上是凸的(或凹的)。
Th2:
(拐点的判别定理1)若在
x
0
x_{0}
x0处
f
′
′
(
x
)
=
0
f''(x) = 0
f′′(x)=0,(或
f
′
′
(
x
)
f''(x)
f′′(x)不存在),当
x
x
x变动经过
x
0
x_{0}
x0时,
f
′
′
(
x
)
f''(x)
f′′(x)变号,则
(
x
0
,
f
(
x
0
)
)
(x_{0},f(x_{0}))
(x0,f(x0))为拐点。
Th3:
(拐点的判别定理2)设
f
(
x
)
f(x)
f(x)在
x
0
x_{0}
x0点的某邻域内有三阶导数,且
f
′
′
(
x
)
=
0
f''(x) = 0
f′′(x)=0,
f
′
′
′
(
x
)
≠
0
f'''(x) \neq 0
f′′′(x)=0,则
(
x
0
,
f
(
x
0
)
)
(x_{0},f(x_{0}))
(x0,f(x0))为拐点。
15.弧微分
dS = 1 + y ′ 2 dx \text{dS} = \sqrt{1 + y'^{2}}\text{dx} dS=1+y′2dx
16.曲率
曲线
y
=
f
(
x
)
y = f(x)
y=f(x)在点
(
x
,
y
)
(x,y)
(x,y)处的曲率
k
=
∣
y
′
′
∣
(
1
+
y
′
2
)
3
2
.
k = \frac{\left| y'' \right|}{{(1 + y'^{2})}^{\frac{3}{2}}}.
k=(1+y′2)23∣y′′∣.
对于参数方程:
{ x = φ ( t ) y = ψ ( t ) , k = ∣ φ ′ ( t ) ψ ′ ′ ( t ) − φ ′ ′ ( t ) ψ ′ ( t ) ∣ [ φ ′ 2 ( t ) + ψ ′ 2 ( t ) ] 3 2 \left\{ \begin{matrix} & x = \varphi(t) \\ & y = \psi(t) \\ \end{matrix} \right.\ ,k = \frac{\left| \varphi'(t)\psi''(t) - \varphi''(t)\psi'(t) \right|}{{\lbrack\varphi'^{2}(t) + \psi'^{2}(t)\rbrack}^{\frac{3}{2}}} {x=φ(t)y=ψ(t) ,k=[φ′2(t)+ψ′2(t)]23∣φ′(t)ψ′′(t)−φ′′(t)ψ′(t)∣
17.曲率半径
曲线在点 M M M处的曲率 k ( k ≠ 0 ) k(k \neq 0) k(k=0)与曲线在点 M M M处的曲率半径 ρ \rho ρ有如下关系: ρ = 1 k \rho = \frac{1}{k} ρ=k1文章来源:https://www.toymoban.com/news/detail-425642.html
[]{#header-n246 .anchor}文章来源地址https://www.toymoban.com/news/detail-425642.html
到了这里,关于机器学习的数学基础(上)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!