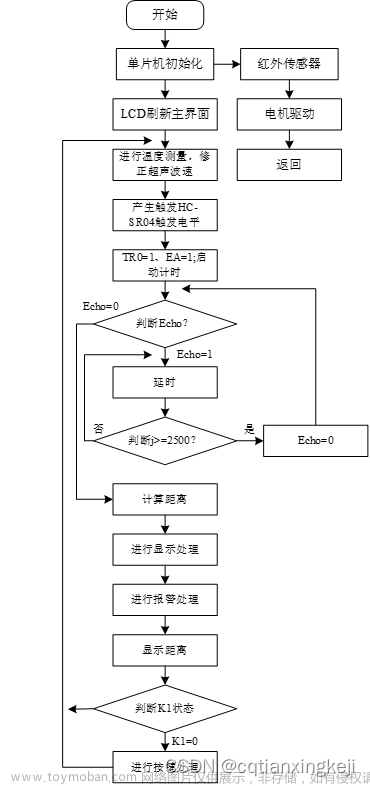
目录
一,广义预测控制
1,概念
2,推导公式
1,E,F丢番图方程求解
2,G,H丢番图方程求解
3,跟踪轨迹
4,求控制律u(t)
二,matlab程序仿真结果
1,matlab程序
2,参数设置
3,仿真结果1
4,仿真结果2
一,广义预测控制
1,概念
广义预测控制,简单来说就是利用历史值去预测系统下一时刻的输出值。
2,推导公式
重点在求解丢番图方程E,F,G
预测模型:

1,E,F丢番图方程求解
预测步长:j
 的矩阵表示如下:
的矩阵表示如下:

j步预测时的丢番图方程:

j+1步预测时的丢番图方程:

式(1-4)减(1-1):

上式左边从0到j-1次的所以幂次项均为零, 和
和 前j项系数相等,可知:
前j项系数相等,可知:

把(1-6)代入式(1-5)中,并展开E,F

令上式左右两边同次幂相等,得递推公式:

递推初值由j=1时的丢番图方程解出。
2,G,H丢番图方程求解 :
:
 的矩阵形式:
的矩阵形式:

其中:
控制时域长度:
最大预测长度:  (
( )
)

同次幂系数相等,得递推公式:

在matlab程序中matrixg_whole矩阵用来缓存计算g和h的数值,随后从matrixg_whole中取出的g_part2即为丢番图方程G矩阵。
3,跟踪轨迹
4,求控制律u(t)
二,matlab程序仿真结果
1,matlab程序:
clear all
clc
close all
%---------------------------------------------------------%
%---GPC算法(水泥 分解炉温度控制)---%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% part 1 参数 %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%仿真时间或者步长(实控的时候 不需要了)
simulationiter1 =100;
simulationiter2 =200;
simulationiter3 = 300;
% 实际系统
a_real=[ 1 0.5];%A(q-1) of process 0.2
b_real=[ 0.5 ];%B(q-1) of process
k_real=1;%time delay of process
%实际系统包含噪声
for i=1:simulationiter3
u(1,i)=0;%init U
noise(1,i)=0*randn()/10;%init random noise
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for i=2:simulationiter3
y_real(1,i)=noise(1,i);%init real y
end%init sum of noise
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%模型参数
% a_model=[1 0.5 0.2 ];%A(q-1) of model
% b_model=[1 0.5 ];%B(q-1) of model
% k_model=1;%time delay of model
a_model = a_real;
b_model = b_real;
k_model = k_real;
na=length(a_model)-1;
nb=length(b_model)-1;
%GPC配置参数%(实控的时候 需要)
GPC_p=6;%predict horizon
GPC_m=6;%control horizon
GPC_lambda=10;%control weight
GPC_alfa=0;%soften parameter 柔化因子
GPC_beta=0;%step scale 阶梯因子 可不用
DMC_sp1 = 5; %设定值
DMC_sp2 = 10; %设定值
DMC_sp3 = 15; %设定值
for i=1:simulationiter1
y_set(1,i)=DMC_sp1;
end%init setpoint of y
for i=(simulationiter1+1):simulationiter2
y_set(1,i)=DMC_sp2;
end%init setpoint of y
for i=(simulationiter2+1):simulationiter3
y_set(1,i)=DMC_sp3;
end%init setpoint of y
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% for i=1:350
% u(1,i)=1;%init U
% noise(1,i)=normrnd(0,0.0);%init random noise
% y_real(1,i)=0;%init real y
% end
% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% for i=1:350
% y_set(1,i)=10;
% end%init setpoint of y
% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% noise_sum(1,1)=noise(1,1);
% for i=2:300
% noise_sum(1,i)=noise_sum(1,i-1)+noise(1,i);
% end%init sum of noise
% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% part 2 init polynomials %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
matrix_e=zeros(k_model+GPC_p-1,1); % E 丢番图方程 (6,1) 生成零矩阵
matrix_f=zeros(na+1,k_model+GPC_p-1); %F 丢番图方程 (2.6)
matrixg_whole=zeros(k_model+GPC_p-1,nb+k_model+GPC_p-1); % G= E*B 丢番图方程
%(6,6)
%计算F 丢番图方程
matrix_f(1,1)=1-a_model(1,2);
for i=1:1:na-1
matrix_f(i+1,1)=a_model(1,i+1)-a_model(1,i+2);
end
matrix_f(na+1,1)=a_model(1,na+1);
%计算E 丢番图方程
matrix_e(1,1)=1;
for j=2:1:k_model+GPC_p-1
matrix_e(j,1)=matrix_f(1,j-1);
matrix_f(1,j)=matrix_f(2,j-1)-matrix_e(j,1)*(a_model(1,2)-1);
for i=1:1:na-1
matrix_f(i+1,j)=matrix_f(i+2,j-1)-matrix_e(j,1)*(a_model(1,i+2)-a_model(1,i+1));
end
matrix_f(na+1,j)=matrix_e(j,1)*a_model(1,na+1);
end%init e,f
%计算G= E*B 丢番图方程
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for i=1:nb+1
matrixg_whole(1,i)=b_model(1,i);
end
for j=2:k_model+GPC_p-1
for i=1:nb+j-1+1
if i<=j-1
matrixg_whole(j,i)=matrixg_whole(j-1,i);
elseif i<=nb+j-1
matrixg_whole(j,i)=matrixg_whole(j-1,i)+matrix_e(j,1)*b_model(1,i-j+1);
elseif i==nb+j
matrixg_whole(j,i)=matrix_e(j,1)*b_model(1,nb+1);
end
end
end%inint g
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for i=1:GPC_p
g_single(1,i)=matrixg_whole(k_model+GPC_p-1,i);
end
for j=1:GPC_p
for i=1:j
g_part(j,i)=g_single(1,j-i+1);
end
end
for j=1:GPC_p
for i=1:GPC_m
g_part2(j,i)=g_part(j,i);
end
end%init g_part for teh use of control of different forms
% 离线计算D矩阵
temp = inv((g_part2)'*(g_part2)+GPC_lambda*eye(GPC_m))*(g_part2)';%inv求逆矩阵
matrix_d = temp(1,:); %取temp第一行
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% part 3 normoal control %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for t=3:simulationiter3
y_real(1,t)=noise(1,t);
% for i=1:1 y_real(1,t)=b_real(1,i)*u(1,t-k_real-i+1)-a_real(1,i+1)*y_real(1,t-i)
% end
for i=1:nb+1
y_real(1,t)=y_real(1,t)+b_real(1,i)*u(1,t-k_real-i+1);
end
for i=1:na
y_real(1,t)=y_real(1,t)-a_real(1,i+1)*y_real(1,t-i);
end%sampleing
y_show = y_real(1,t)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for i=0:GPC_p-1
y1(i+1,1)=0;
for l=1:na+1
y1(i+1,1)=y1(i+1,1)+matrix_f(l,i+k_model)*y_real(1,t-l+1);
end
for l=i+2:nb+k_model+i
y1(i+1,1)=y1(i+1,1)+matrixg_whole(k_model+i,l)*(u(1,t+i+1-l)-u(1,t+i-l));
end
end%init y1
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
w_start=0;
if k_model==1
w_start=y_real(1,t);
else
for l=1:na+1
w_start= w_start+matrix_f(l,k_model-1)*y_real(1,t-l+1);
end
for l=1:nb+k_model-1
w_start= w_start+matrixg_whole(k_model-1,l)*(u(1,t-l)-u(1,t-l-1));
end%init w_start
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
w(1,1)=GPC_alfa*w_start+(1-GPC_alfa)*y_set(1,t);
for i=1:GPC_p-1
w(i+1,1)=GPC_alfa*w(i,1)+(1-GPC_alfa)*y_set(1,t);
end%init w
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
u_delta = matrix_d *(w-y1)
u(1,t)=u(1,t-1)+u_delta;%get u if you choose normal gpc
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% part 4 plot the result %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
subplot(2,1,1),plot(y_set,'r');hold on;plot(y_real,'b');legend('设定值','输出值');hold on;axis([0,simulationiter3-10,-inf,inf])
subplot(2,1,2),plot(u,'g');legend('控制律');hold on;axis([0,simulationiter3-10,-inf,inf])2,参数设置:
3,仿真结果1:

4,仿真结果2:
最大预测长度:2
控制时域长度:1
 文章来源:https://www.toymoban.com/news/detail-425986.html
文章来源:https://www.toymoban.com/news/detail-425986.html
由仿真结果可知:预测长度j越长,预测输出值越准确,响应越快,但阶数越高,对计算要求越高。文章来源地址https://www.toymoban.com/news/detail-425986.html
到了这里,关于广义预测控制(GPC,含公式推导和仿真截图)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!