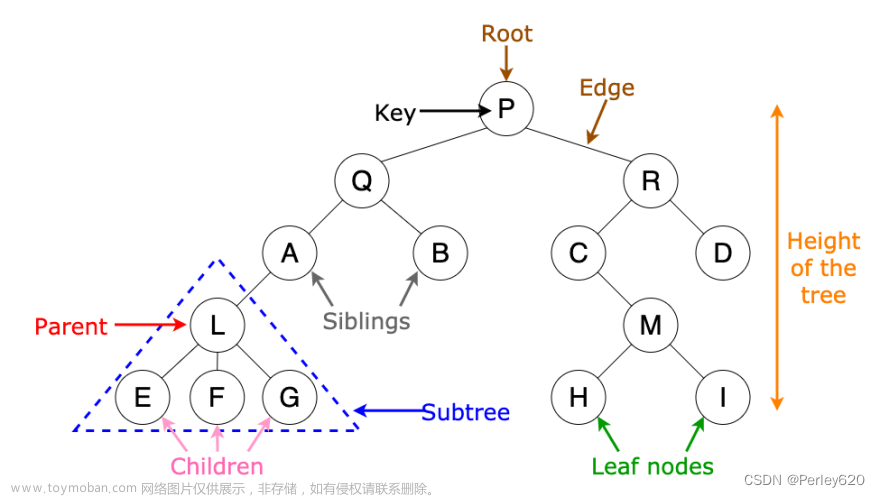
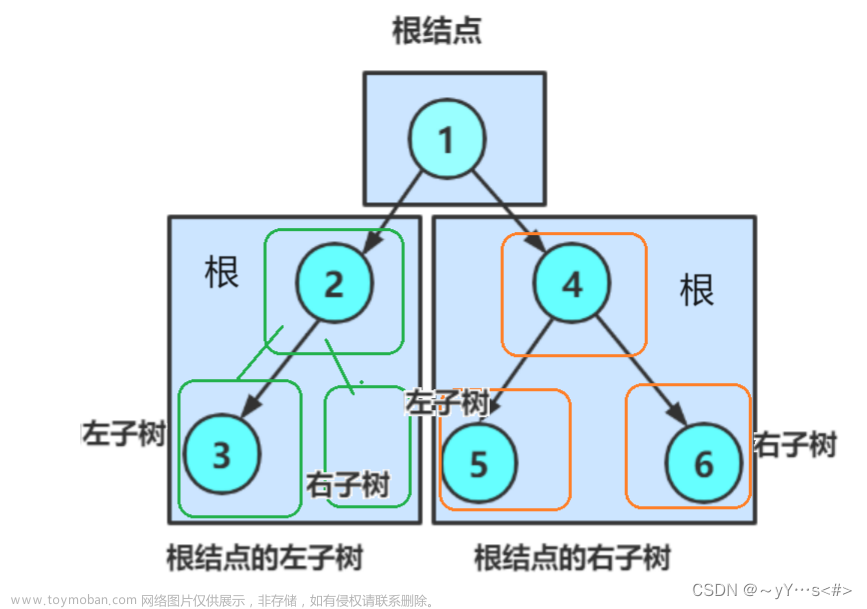
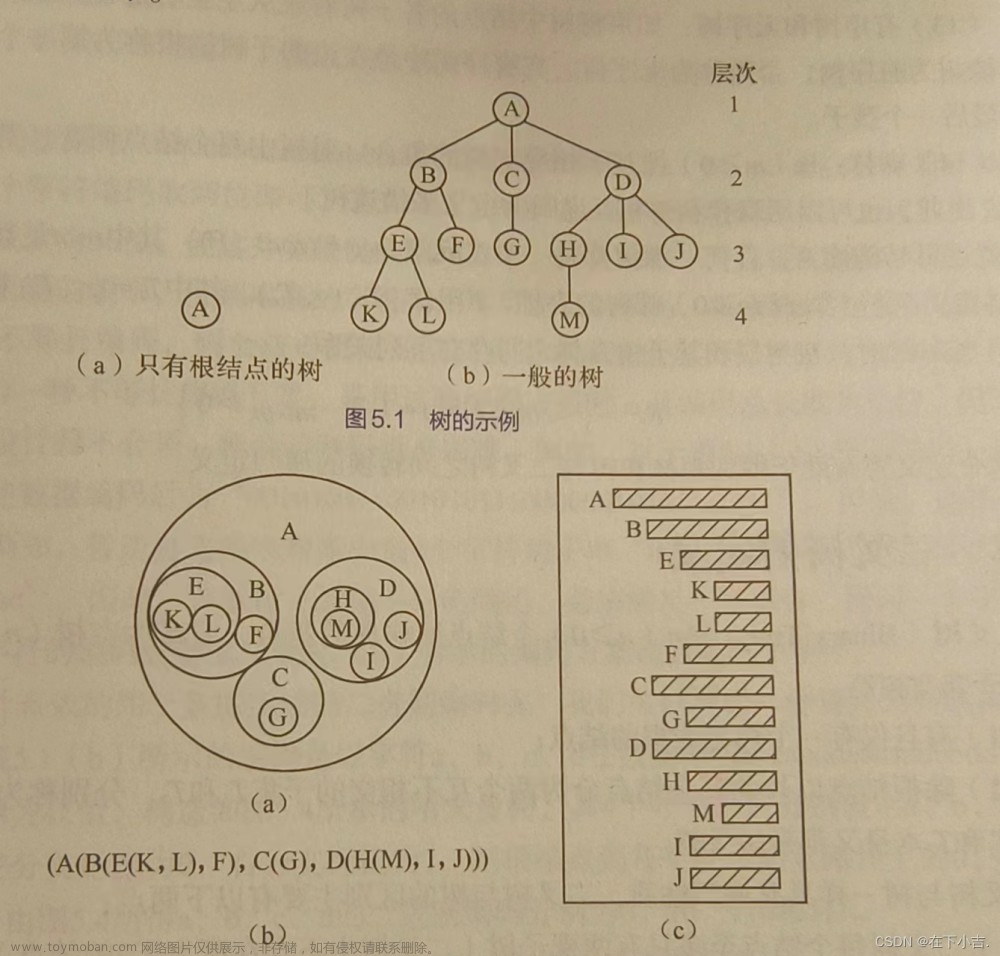
二叉树遍历是二叉树的一种重要操作 必须要掌握
二叉树的遍历可以用递归和非递归两种做法来实现
递归做法
前序遍历
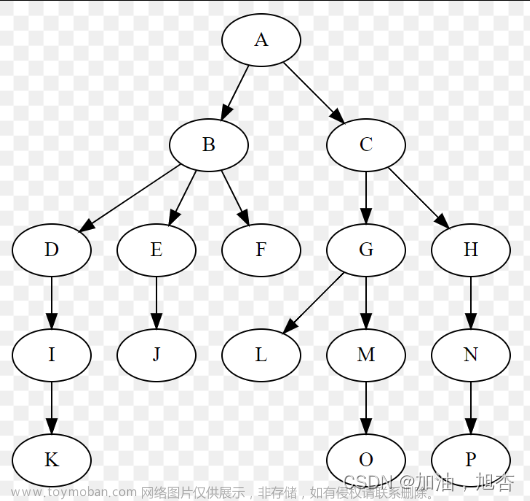
前序遍历的遍历方式是先根节点 在左节点 在右节点
述这棵树前序遍历的结果是:A B D E C F G
递归的思想就是把问题拆分成一个个小问题来解决
public void preOrder(treeNode root) {
if (root == null) return;
System.out.print(root.val + " ");
preOrder(root.left);
preOrder(root.right);
//前序遍历 先打印根节点 在打印左节点 在打印右节点
//将大问题拆分成小问题 递归解决
}
treeNode是一个内部类 具体实现
public static class treeNode {
treeNode left;
//左节点
treeNode right;
//右节点
int val;
//值
public treeNode(int val) {
this.val = val;
}
}
中序遍历
中序遍历的顺序是先左 在根 在右
**递归实现的代码都十分相似 **
public void inOrder(treeNode root) {
if (root == null) return;
inOrder(root.left);
System.out.print(root.val + " ");
inOrder(root.right);
//和前序遍历相比 只是递归的顺序改变了
//和遍历的顺序一样
//先左 在根 在右
}
后序遍历
后序遍历的顺序是先左 在右 在根
public void postOrder(treeNode root) {
if (root == null) return;
inOrder(root.left);
inOrder(root.right);
System.out.print(root.val + " ");
//只是顺序发生了改变
}
非递归
前序遍历
我们不采用递归的方式 但是要模拟递归的思路
非递归实现 我们要借用栈这个数据结构
例如这颗树 我们用它举例
模拟递归 我们第一步肯定是先遍历左树 直到遍历到叶子节点
因为我们是前序遍历 所以每向下遍历一次就记录下来这个节点的值(可以是打印 也可以放在其他集合中)然后把这个节点放在栈中

此时我们的cur指针指向了D节点的左子节点位置 此时发现cur现在为空 说明我们已经到达左树的最底部此时我们要看D节点有没有右子节点 因为我们的顺序是(根左右)
但是我们的cur已经指向了D节点的左子树,而且二叉树是单向的 我们怎么能找到D节点呢?
此时栈就起到了作用 因为我们每打印一次就把这个节点压入栈中 此时栈顶元素是D节点 我们可以弹出栈顶元素D 然后把弹出来的元素赋值给cur 在使cur指向D的右树 即
cur = stack.pop();
cur = cur.right;
然后在执行上述的操作遍历左树
根据上面的思想我们可以写出大体逻辑
public void preOrderNor(TreeNode root) {
if(root == null) return;
Stack<TreeNode> stack = new Stack<>();
//创建一个栈来存放元素
TreeNode cur = root;
//定义指针
//这个循环内就是我们刚才的思路
while (cur != null) {
stack.push(cur);
System.out.print(cur.val + " ");
cur = cur.left;
}//这个循环就是一直遍历左数直到左子树被遍历完
TreeNode top = stack.pop();
cur = top.right;
//弹出栈顶元素 cur赋值栈的右子树
}
但是我们可以看到 我们还没有分析出来最外层循环的出口 即什么时候这棵二叉树就完成了遍历?
首先我们要思考一个问题 当cur等于D的右子节点的时候 cur此时需不需要入栈? 答案是肯定需要的 那么 我们入栈的代码应该怎么写呢?
因为我们入栈后 还需要继续遍历左子树直到遍历完全部的左节点 所以这里肯定是一个循环 我们需要在这个循环的外部在嵌套一层循环 那么我们循环的条件就可以写成cur!=null 因为只有!=null时 内层的循环才可以执行 也就是才可以入栈
public void preOrderNor(TreeNode root) {
if(root == null) return;
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root;
while (cur != null) {
while (cur != null) {
stack.push(cur);
System.out.print(cur.val + " ");
cur = cur.left;
}
//cur == null
TreeNode top = stack.pop();
cur = top.right;
}
}
**这段代码还有一个问题 我们外层的循环条件是cur!=null 但是我们在cur获取到D的右子节点时 此时cur又为空了 此时循环条件不满足 循环就结束了 但是我们还没有遍历完这棵二叉树 我们还有什么依据来继续循环呢? **
此时就要用到我们的栈 此时栈中还有元素 说明二叉树还没有遍历完 所以循环条件还要加栈不为空才可以
public void preOrderNor(TreeNode root) {
if(root == null) return;
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root;
while (cur != null || !stack.empty()) {
while (cur != null) {
stack.push(cur);
System.out.print(cur.val + " ");
cur = cur.left;
}
//cur == null
TreeNode top = stack.pop();
cur = top.right;
}
}
我们加了这个条件之后 此时进入循环 cur = top.right 此时栈顶元素是B节点 cur此时指向B节点的右子节点 此时整棵树就可以串起来 遍历结束了
此时我们的二叉树的前序非递归遍历就结束了
中序遍历
中序遍历的思路和前序遍历基本一致 只需要改变打印的位置即可
前序遍历我们因为要先打印根节点 所以在找左子树的最后一个节点的位置时 每次循环都打印 这样就可以先打印出来根节点
中序遍历需要先打印左节点 在打印根节点 所以需要们在最后到了底部的时候再去打印节点即可 其他代码不需要改变
public void preOrderNor(TreeNode root) {
if(root == null) return;
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root;
while (cur != null || !stack.empty()) {
while (cur != null) {
stack.push(cur);
cur = cur.left;
}
//cur == null
TreeNode top = stack.pop();
System.out.print(cur.val + " ");
cur = top.right;
}
}
后序遍历
后续遍历的情况比上面两种情况就更复杂
在上面的代码的主体框架下 要对更多情况进行考虑
首先不能再遍历左子树的时候就进行打印操作 不管是到树的底部打印还是每遍历一次就打印一次 因为后序遍历是先左 后右 在根节点
我们再走到左子树的最底部的左节点时 也就是下图的情况
cur指向D节点的左子节点 此时我们还要判断他有没有右子节点 因为右子节点的打印优先级高于根节点 如果右节点也为空 此时在打印D
且我们还需要注意的一点是 前序和中序遍历时都只需要判断左树是否为空 所以压入栈的元素只需要出一次栈即可完成目的
但是后序遍历我们不仅要判断左树是否为空 还需要判断右树是否为空 如果在判断左树时就把栈顶元素弹出 在判断右树是否为空是 就没有元素判断 所以在判断左树是否为空时 只需要peek元素 在判断完右树的元素时 在弹出元素
代码大致如下
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> ret = new ArrayList<>();
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root;
while(cur != null || !stack.empty()){
while(cur != null){
stack.push(cur);
cur = cur.left;
}
TreeNode top = stack.peek();
if(top.right == null){
ret.add(top.val);
stack.pop();
}else{
cur = top.right;
}
}
return ret;
}
}
//这里没有打印元素 而是将元素放进一个集合中 和打印思路相同
此时代码还有一点点小问题
根据上面的思路写出代码 我们根据代码遍历一次
当cur = D 时 此时cur不为空 cur = D的左节点 此时cur为空 peek出栈顶元素D 检查D的右树是否为空 发现是空 此时将D的值放入一个集合 把D弹出栈
遍历到这步还没有问题 当我们在进入循环cur还是= D 又进行了刚才 的操作 我们发现在这里出现了死循环 只能在D这个节点处遍历
根本问题就是 我们已经打印过D了 所以D不需要进入判断 所以判断条件不仅是top.
right == null 在这个节点打印过的时候 也应该进入else文章来源:https://www.toymoban.com/news/detail-426082.html
代码如下文章来源地址https://www.toymoban.com/news/detail-426082.html
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> ret = new ArrayList<>();
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root;
TreeNode prev = null;
while(cur != null || !stack.empty()){
while(cur != null){
stack.push(cur);
cur = cur.left;
}
TreeNode top = stack.peek();
if(top.right == null || top.right == prev){
prev = top;
ret.add(top.val);
stack.pop();
}else{
cur = top.right;
}
}
return ret;
}
}
到了这里,关于【Java数据结构】二叉树的前中后序遍历(递归和非递归)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!