多因素方差分析-Toy模板网

这篇具有很好参考价值的文章主要介绍了多因素方差分析。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

理论依据

【基本思想】

1.多因素方差分析的基本思想

方差分析中当涉及两个或两个以上的分类型自变量时，则需要进行多因素方差分析。进行多因素方差分析时，要首先确定因变量和若干个自变量，其次分析数值型因变量的方差，最后分别比较因变量总离差平方和各部分所占比例，进而推断自变量以及自变量的交互作用是否给因变量带来了显著影响。

多因素方差分析将因变量观测值的总变差分解为三个组成部分：自变量独立作用的影响，自变量交互作用的影响和随机因素的影响。以双因素方差分析为例，即SST=SSA+SSB+SSAB+SSE。式中,SST为因变量的总变差:SSA和SSB分别为自变量A和B独立作用引起的变差；SSAB为自变量A和B两两交互作用引起的变差；SSE为随机因素引起的变差。通常称SSA+SSB为主效应，SSAB为交互效应，SSE为剩余变差。

2.多因素方差分析的理论假设

(1)各因素条件下的样本是随机的。

(2)各因素条件下的样本是相互独立的。

(3)各因素条件下的样本来自正态总体，且样本方差具有方差齐性。

3.多因素方差分析的基本步骤

(1)提出原假设。多因素方差分析的原假设是：各自变量不同水平下的因变量总体的均值无显著差异，自变量各效应和交互作用效应同时为0。

(2)选择检验统计量。多因素方差分析中采用的检验统计量为F统计量。

(3)计算检验统计量的值及相应的P值。

(4)给定显著性水平，并做出决策。给定显著性水平，依次与各个检验统计量的P值进行比较。如果P值小于显著性水平，则应拒绝原假设；如果P值大于或等于显著性水平，则没有理由拒绝原假设。

【实验目的】

1.准确理解多因素方差分析的方法原理。

2.熟练掌握多因素方差分析的SPSS操作。

3.能够运用多因素方差分析方法解决身边的实际问题。

实验内容

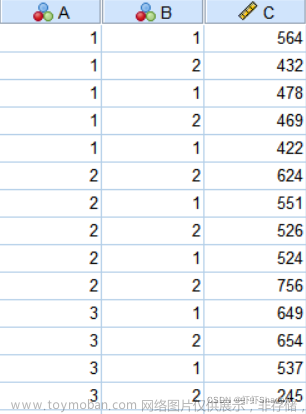
2006年全国五省的一项调查显示，企业的担保方式和信用程度对企业获得的贷款金额具有显著影响，此次调查所获得的部分数据，如数据集data11-1所示，此数据集包含担保方式，信用等级，贷款金额，其中担保方式和信用等级为定类变量。变量担保方式有五个取值。1=实物抵押担保，2=质押担保，3=信用担保，4=保证担保，5=业主个人担保。变量信用等级有两个取值：1=好，2=差。试分析本次调查中，主要担保方式和信用等级两个变量对变量贷款金额的影响是否显著，如果显著，再分析各个因素的不同水平对其影响是否显著。

操作步骤

实验中以担保方式和信用等级为自变量，贷款金额为因变量。其中的原假设为：不同担保方式没有对贷款金额产生显著影响；不同信用等级没有对贷款金额产生显著影响；担保方式和信用等级没有对贷款金额产生显著的交互影响。

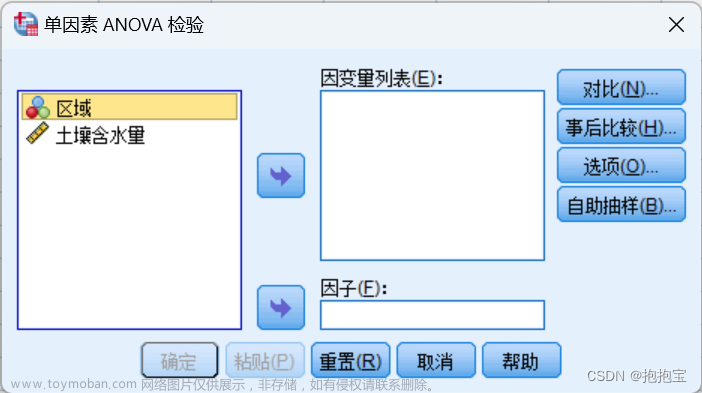
1）选择菜单:【Analyze】→【General Linear Model】→【Univariate】,弹出图3-1所示的对话框。

图3-1：选择菜单步骤

2）选择贷款金额[x3]到“Dependent Variable”框中,选择担保方式[x1]和信等级[x2]到“Fixed Factor(s)”框中。

图3-2：“Univariate”对话框

3）点击“Model”按钮,弹出如图3-3所示的对话框。

4）在“Specify Model”框下选择“Full factorial”选项。“Full factorial”为全模型选项，这是系统默认的选项。全模型分析中包括所有自变量的主效应和因素与因素之间的交互效应。自定义模型(Custom)是针对全模型而言的。如果研究中发现自变量的某阶交互作用没有给因变量带来显著影响，则可尝试建立自定义模型。对于自定义模型，其参数估计的方法、检验统计量与全模型相似。本实验中选用全模型。单击“Continue”按钮返回主对话框。

图3-3：“Model”对话框

5）点击“Options”按钮,弹出如图3-4所示的对话框。选择“Display”框下的“Homogeneity tests”选项进行方差齐性检验。点击“Continue”,返回主对话框。

图3-4：“Options”对话框

6）在主对话框中点击“Post Hoc”按钮，弹出如图3-5所示的对话框。在此对话框中选择x1和x2进入“Post Hoc Tests for”框内;选择“Equal VariancesAssumed”框下的“LSD”选项。

图3-5：“Post Hoc”对话框

7）点击【Continue】→【OK】,系统输出分析结果如下文所示。

结果分析

表3-1中给出了方差同质性检验结果。基于平均值来看，F统计量的值为0.245，P值为0.986，所以认为各组的方差相等，即满足方差齐性这一条件；基于中位数来看，因为P值为0.989 > 0.05，所以认为各组的方差相等，即满足方差齐性这一条件；基于中位数和调整后的 df来看，因为P值为0.989 > 0.05，所以认为各组的方差相等，即满足方差齐性这一条件；基于截尾平均值来看，因为P值为0.986 > 0.05，所以认为各组的方差相等，即满足方差齐性这一条件。

表3-1：方差同质性检验输出结果

Levene's Test of Equality of Error Variancesa,b
		Levene Statistic	df1	df2	Sig.
贷款金额	Based on Mean	.245	9	70	.986
	Based on Median	.229	9	70	.989
	Based on Median and with adjusted df	.229	9	69.236	.989
	Based on trimmed mean	.245	9	70	.986
Tests the null hypothesis that the error variance of the dependent variable is equal across groups.
a. Dependent variable: 贷款金额
b. Design: Intercept + x1 + x2 + x1 * x2

贷款金额值=观测变量均值（截距）+担保方式引起的变动+信用等级引起的变动+担保方式与信用等级交互作用引起的变动+抽样误差。

表3-2为单变量双因素方差分析表，担保方式x1作用的F统计量的值是11.634，P值为0.000。信用水平x2作用的F统计量的值是488.686,P值为0. 000。由担保方式x1和信用水平x2交互作用的F统计量的值是0.010，P值为1.000。

因为担保方式、信用等级的显著性为0.000 < 0.05 ，所以可以认为担保方式、信用等级对销售额的影响是显著的，又因为担保方式与信用等级交叉的显著性为1.000 > 0.05 ，所以可以认为促销方式与售后服务的交互效应是不显著的。

表3-2：单变量双因素方差分析表

Tests of Between-Subjects Effects
Dependent Variable: 贷款金额
Source	Type III Sum of Squares	df	Mean Square	F	Sig.
Corrected Model	4560586.362a	9	506731.818	59.474	.000
Intercept	20929557.013	1	20929557.013	2456.440	.000
x1	396513.675	4	99128.419	11.634	.000
x2	4163737.513	1	4163737.513	488.686	.000
x1 * x2	335.175	4	83.794	.010	1.000
Error	596419.625	70	8520.280
Total	26086563.000	80
Corrected Total	5157005.987	79
a. R Squared = .884 (Adjusted R Squared = .869)

由于本数据中的方差齐性检验结果是具有方差齐性的，所以，应就LSD的输出结果进行分析。比较相应的两组均值的P值与显著性水平的大小。在0.05的显著性水平下，如果P值 ≥ 0.05，则两组均值不存在显著性差异；如果P值 < 0.05，则两组均值存在显著性差异。

下表中给出了担保方式对贷款金额影响的多重比较的结果，从中可以看出，质押担保与实物抵押担保、质押担保与信用担保、保证担保与信用担保、保证担保与业主个人担保的显著性P值 > 0.05，说明这几组之间的差异不显著，而其他各组之间之间的差异显著。

表3-3：多重比较输出结果

Multiple Comparisons
Dependent Variable: 贷款金额
LSD
(I) 担保方式	(J) 担保方式	Mean Difference (I-J)	Std. Error	Sig.	95% Confidence Interval
(I) 担保方式	(J) 担保方式	Mean Difference (I-J)	Std. Error	Sig.	Lower Bound	Upper Bound
实物抵押担保	质押担保	49.31	32.635	.135	-15.78	114.40
	信用担保	100.25*	32.635	.003	35.16	165.34
	保证担保	151.44*	32.635	.000	86.35	216.53
	业主个人担保	197.81*	32.635	.000	132.72	262.90
质押担保	实物抵押担保	-49.31	32.635	.135	-114.40	15.78
	信用担保	50.94	32.635	.123	-14.15	116.03
	保证担保	102.12*	32.635	.003	37.04	167.21
	业主个人担保	148.50*	32.635	.000	83.41	213.59
信用担保	实物抵押担保	-100.25*	32.635	.003	-165.34	-35.16
	质押担保	-50.94	32.635	.123	-116.03	14.15
	保证担保	51.19	32.635	.121	-13.90	116.28
	业主个人担保	97.56*	32.635	.004	32.47	162.65
保证担保	实物抵押担保	-151.44*	32.635	.000	-216.53	-86.35
	质押担保	-102.12*	32.635	.003	-167.21	-37.04
	信用担保	-51.19	32.635	.121	-116.28	13.90
	业主个人担保	46.38	32.635	.160	-18.71	111.46
业主个人担保	实物抵押担保	-197.81*	32.635	.000	-262.90	-132.72
	质押担保	-148.50*	32.635	.000	-213.59	-83.41
	信用担保	-97.56*	32.635	.004	-162.65	-32.47
	保证担保	-46.38	32.635	.160	-111.46	18.71
Based on observed means. The error term is Mean Square(Error) = 8520.280.
*. The mean difference is significant at the .05 level.文章来源地址https://www.toymoban.com/news/detail-426505.html