KMP算法【C++实现】-Toy模板网

这篇具有很好参考价值的文章主要介绍了KMP算法【C++实现】。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

BF算法

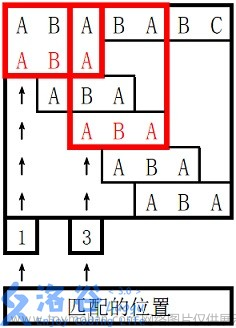
字符串匹配，我们一般思路是被对比的串作为主串，对主串的的每一个字符串作为子串的开头，与要匹配的字符串进行匹配，匹配不成功则子串开头+1，要匹配的字符串回溯到1，进行匹配，直到匹配成功或者主串全部遍历完成，这就是BF算法。

分析时间复杂度，假设主串长度为n，匹配字符串长度为m，当第一次就匹配上的时候，执行1次，复杂度为O(1)，最后一次才匹配到并且每次匹配都是最后一位才判断出不符合，复杂度为O((n-m+1)*m),平均复杂度太高了，效率非常低。

基于此，我们找到了一个新的匹配模式，即KMP算法。

KMP算法概念

KMP算法的基本思路是主串不回溯，子串部分回溯，通过对主串进行至多一次遍历即可判定字符串是否有匹配的值。

现在我们假定给出一个主串arr：

a b a b d a b a b c

一个子串brr：

a b a b c

很明显在第一次匹配时，子串和主串的前四个字符匹配成功，即a b a b，到第五个字符c，和主串第五个d不匹配，按照朴素匹配算法，我们要将主串回溯到第二个位置b，子串回溯到第一个位置a，重新进行匹配，复杂度很高。

观察后我们发现，主串第三四个字符其实是和子串第一二个字符是重合的，那么我们如果能找出一种方法，让字符串在匹配的时候直接略过重合的部分【也就是子串1 2 位置和主串3 4 位置】向后比较,那么时间复杂度会大大降低。

一个简单的例子就是上面假定给出的主串和子串，按照我们预计的这种算法，第一次匹配时第五个字符不匹配，前四个是相同的，而三四个字符等于子串一二个字符，所以第二次匹配时子串跳到第三个字符，主串跳到第五个字符进行比较，比较失败，第三次匹配子串回到第一个位置，主串跳到第六个位置，五个字符全部相同，匹配完成。

这趟匹配中，使用BF算法下我们要匹配五次，比较5+1+3+1+1+5次，而KMP算法下我们仅需要匹配三次，比较5+1+5次，当子串足够长的时候，KMP算法的优越性就显而易见了。

对KMP算法的解释

通俗的来说，KMP算法就是通过寻找子串中前后最大相同子串【也就是相同前后缀】来减少比较次数。

别急，我们举一个小子串的例子来帮助大家理解。

a b a b

它的最长相同前后缀就是a b。

理解了这个概念基本就可以掌握kmp算法了。回到我么们最上方蓝色字体的子串主串，在第二次匹配的时候我们是通过子串跳到3，主串跳到5来减少比较次数的，思考为什么可以这样做。

其实就是主串第三四个字符，a b，与子串中前两个字符是相同的，所以我们跳过了这个我们已知的这部分匹配。

一个简单的初中数学，arr[2]+arr[3] == brr[2]+brr[3] , brr[2]+brr[3] == brr[0]+brr[1],所以arr[2]+arr[3] == brr[0]+brr[1],对吧？那么我们向arr[1] arr[2] 和 brr[1] brr[2]之间添加一个长度为n的相同的无规则字符串，这依然不影响我们上边的结论，也就是主串最后匹配的两个字符等于子串的前两个字符，所以我们可以跳过中间的一串，并提前将子串前两个和主串后两个重合。

KMP算法【C++实现】

这就是匹配过程，相比BF算法，节省了两次匹配的时间，当长度变长，减少的匹配次数会更多

那么KMP算法到现在就很清晰了，就是找到了子串所有子集的最长前后缀嘛，也就是说KMP算法的本质就是寻找子串的最长前后缀。

比如如果一个子串除去了最后一个字符【也就是这个子串的最大真子集】的最长前后缀是2，且这个子串正好比较到最后一个才发现不匹配，我们就可以直接跳过子串中的前两个，从子串第三个开始和主串匹配失败的那个开始作比较，因为最大真子集子串倒数两个字符等于子串前两个字符，而最大真子集子串最后两个字符和主串对应位置的字符匹配成功了嘛【可以去看蓝色字体的主串子串帮助理解】

只有当最后一个字符匹配失败才能用这个方法未免应用面太狭隘了，进一步思考可以想到，当倒数第二个字符匹配失败的时候，我们可以去找去除最后两个字符的子串子集的最大前后缀，倒数第三个字符匹配失败就去找去除最后三个字符的子串子集的最大前后缀......直到第一个第一个字符匹配失败，就可以子串不动，主串+1去匹配。我们可以用一个next数组来储存每一个子串子集的最长前后缀。

next数组的意义和求法

实际上next数组中存储的数据就是这个子串中长度为下标+1的子串子集的最大前后缀长度。

老样子，我们上个例子来帮助理解 a b a b c

对于这个子串，长度为一的子串子集就是a,它只有一个字符，所以最长前后缀没有意义，next[0]=0；

长度为二的子串子集是a b，他最后一个字符和第一个字符不同，next[1]=0;

长度为三的子串子集是a b a，它最后一个字符和第一个字符相同，next[2]=1;

长度为四的子串子集是a b a b,它倒数两个字符和前两个字符相同，next[3]=2;

长度为五的子串子集是a b a b c,它前后没有字符串相同，next[4]=0;

所以该子串的next数组就是0 0 1 2 0

这个数组内容其实除了表示最长相同前后缀，还表示匹配失败时应该跳回到子串的第几个位置进行比较，比如当第五个字符匹配失败时，我们找到长度为四的子串子集的最大相同前后缀，也就是next[3]，它=2，所以在下一次匹配，我们可以直接把子串跳过子串[0]和子串[1]，从子串[2]开始比较【也就是第三个字符】。

对于next数组的求解，我们可以进一步优化一下，不用每次都把子串子集所有前后缀都比较一遍，实际上，观察上边的next数组我们可以发现next数组的值最多只比前一个数值多一，这也很好理解，向前一个字符串的后边增加一个字符，它只在最后添加的字符等于之前字符串第最长相同前缀+1 个字符时，它的最长前后缀长度才会+1，否则直接归零，所以我们只要看前一个next的值，再判断一次，就可以求出该next值。

话不多说，上代码：求解next数组，返回数组地址

int* renext(string one)
{
    int* nextarr = new int[one.length()+2];
    nextarr[0] = 0;
    for (int i = 1; i < one.length(); i++)
    {
        if (nextarr[i - 1] == 0)//如果前一个next为0，则这个只可能是0或1
        {
            if (one[i] == one[0])
                nextarr[i] = 1;
            else
                nextarr[i] = 0;
        }
        else//不然就是上一个next的数值+1或0
        {
            if (one[i] == one[nextarr[i-1]])
                nextarr[i] = nextarr[i - 1] + 1;
            else
                nextarr[i] = 0;
        }
    }
    return nextarr;
}

KMP算法函数代码：

int KMPsf(string all, string one)
{
    int cs1 = 0;//匹配成功个数
    int* nextarr = renext(one);
    int x = 0;
    while (x < all.length() && cs1 != one.length())//当没有对主串all全部遍历并且没有成功匹配时
    {
        if (all[x] == one[cs1])
            cs1++;
        else
            cs1 = nextarr[cs1];
        x++;
    }
    if (cs1 == one.length())//cs1即是匹配成功的字符数量，当与子串长度一致时就匹配成功
        cout << "yes" << endl;
    else
        cout << "no" << endl;
    return 0;
}

完整代码：

#include<iostream>
#include<string>
using namespace std;
//KMP算法
int* renext(string one)
{
    int* nextarr = new int[one.length()+2];
    nextarr[0] = 0;
    for (int i = 1; i < one.length(); i++)
    {
        if (nextarr[i - 1] == 0)
        {
            if (one[i] == one[0])
                nextarr[i] = 1;
            else
                nextarr[i] = 0;
        }
        else
        {
            if (one[i] == one[nextarr[i-1]])
                nextarr[i] = nextarr[i - 1] + 1;
            else
                nextarr[i] = 0;
        }
    }
    return nextarr;
}
int KMPsf(string all, string one)
{
    int cs1 = 0;//匹配成功个数
    int* nextarr = renext(one);
    int x = 0;
    while (x < all.length() && cs1 != one.length())//当没有对主串all全部遍历并且没有成功匹配时
    {
        if (all[x] == one[cs1])
            cs1++;
        else
            cs1 = nextarr[cs1];
        x++;
    }
    if (cs1 == one.length())//cs1即是匹配成功的字符数量，当与子串长度一致时就匹配成功
        cout << "yes" << endl;
    else
        cout << "no" << endl;
    return 0;
}
int main()
{
    string all;
    string one;
    cin >> all >> one;
    KMPsf(all, one);
    return 0;
}

为了减少一个匹配算法的时间复杂度，我们居然还要再写第二个匹配算法算出一个数组，这不能不说有一种奇妙的幽默在里面。但分析一下，我们假设主串长度为n，子串长度为m，求mext数组的时间复杂度仅仅只有O(m)，因为后边匹配中主串不回溯，最多匹配n次，我们就按最坏匹配n次算，KMP算法的时间复杂度仅仅是O(m+n)，可以看出时间复杂度降低的幅度是非常大的，而空间上仅仅增加了一个next数组，这实在是太实惠了。文章来源地址https://www.toymoban.com/news/detail-426671.html

到了这里，关于KMP算法【C++实现】的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！