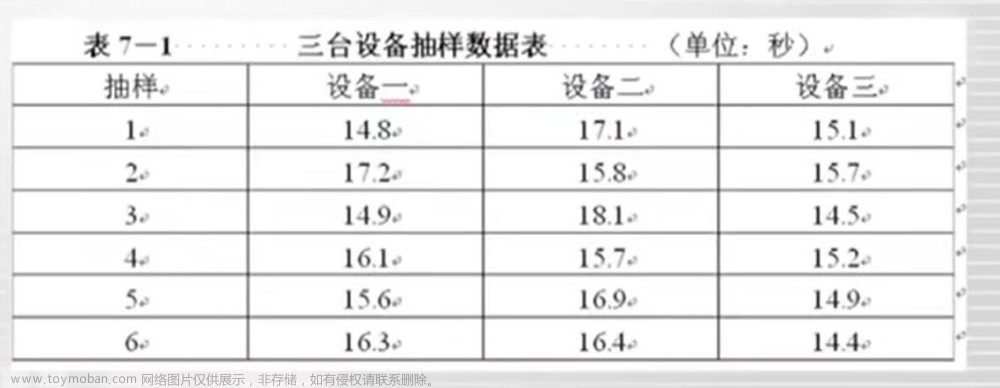
一、考点归纳
二、练习题1写出下列随机试验的样本空间：
（1）记录某班一次统计学测验的平均分数；
（2）某人在公路上骑自行车，观察该骑车人在遇到第一个红灯停下来以前遇到绿灯的次数；
（3）生产产品直到有10件正品为止，记录生产产品的总件数。
解：（1）平均分数是范围在0～100之间的一个连续变量，所以平均分数的样本空间Ω＝[0，100]。
（2）遇到的绿灯次数是从0开始的任意自然数，所以样本空间Ω＝N。
（3）之前生产的产品中可能无次品也可能有任意多个次品，所以样本空间Ω＝{10，11，12，13，…}。
2某人花2元钱买彩票，他抽中100元奖的概率是0.1%，抽中10元奖的概率是1%，抽中1元奖的概率是20%，假设各种奖不能同时抽中，试求：
（1）此人收益的概率分布。
（2）此人收益的期望值。
解：（1）设X为此人的收益，抽中100元奖时的收益为100－2＝98（元），抽中10元奖时的收益为10－2＝8（元），抽中1元奖时赔1元，抽中0元奖时赔2元，则此人收益的概率分布为：
P（X＝98）＝0.001
P（X＝8）＝0.01
P（X＝－1）＝0.2
P（X＝－2）＝1－P（X＝98）－P（X＝8）－P（X＝－1）＝0.789
（2）E（X）＝98×0.001＋8×0.01＋（－1）×0.2＋（－2）×0.789＝1.6
3设随机变量X的概率密度为：
f（x）＝3x2/θ3，0＜x＜θ
（1）已知P（X＞1）＝7/8，求θ的值。
（2）求X的期望值与方差。
解：（1）由P（X＞1）＝7/8可得：P（X≤1）＝1－P（X＞1）＝1/8，即
解得：θ＝2。所以，随机变量X的概率密度为：f（x）＝3x2/8，0＜x＜2。
（2）由X的概率密度可得期望值为：
又
因此
4一张考卷上有5道题目，同时每道题列出4个备选答案，其中有一个答案是正确的。某学生凭猜测能答对至少4道题的概率是多少？
解：设X为答对题的数目。由题意知，答对一道题的概率为1/4。那么X～B（5，1/4），于是答对至少4道题的概率为：
5设随机变量X服从参数为λ的泊松分布，且已知P{X＝1}＝P{X＝2}，求P{X＝4}。解：由泊松分布的公式有：
P（X＝1）＝λe－λ
P（X＝2）＝λ2e－λ/（2！）
由P{X＝1}＝P{X＝2}，解得：λ＝2。
因此P（X＝4）＝24×e－2÷4！＝2/（3e2）。
6设X～N（3，4），试求：（1）P{|X|＞2}；（2）P{X＞3}。
解：（1）
（2）由于N（3，4）关于均值3对称，所以P{X＞3}＝1/2。
7一工厂生产的电子管寿命X（以小时计算）服从期望值μ＝160的正态分布，若要求P{120＜X＜200}≥0.08，允许标准差σ最大为多少？
解：由
可得：Φ（40/σ）≥0.54，查表得：40/σ≥0.1004，故σ≤398.41。即允许标准差σ最大为398.41。8一本书排版后一校时出现错误处数X服从正态分布N（200，400），求：
（1）出现错误处数不超过230的概率。
（2）出现错误处数在190～210之间的概率。
解：（1）出现错误处数不超过230的概率为：
（2）出现错误处数在190～210之间的概率为：文章来源：https://www.toymoban.com/news/detail-426777.html
文章来源地址https://www.toymoban.com/news/detail-426777.html
到了这里，关于《统计学》第八版贾俊平第五章概率与概率分布的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
