初级算法-回溯算法

主要记录算法和数据结构学习笔记，新的一年更上一层楼！

• 回溯算法是递归的副产品，是一种搜索的方式。本质是穷举，可加剪枝操作
• 可抽象为树形结构，集合大小构成树的宽度，递归的深度，都构成树的深度

1.组合：N个数里面按一定规则找出k个数的集合
2.分割：一个字符串按一定规则有几种切割方式
3.子集：一个N个数的集合里有多少符合条件的子集
4.排列问题：N个数按一定规则全排列，有几种排列方式
5.棋盘问题：N皇后，解数独


回溯算法模版框架：

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

一、组合

1.题目：给定两个整数 n 和 k，返回 1 … n 中所有可能的 k 个数的组合。

示例: 输入: n = 4, k = 2 输出: [ [2,4], [3,4], [2,3], [1,2], [1,3], [1,4], ]

2.解题思路：

//组合（优化）
var combine = function(n, k) {
    const res = [], path = [];
    backtracking(n, k, 1);
    return res;
    function backtracking (n, k, i){
        const len = path.length;
        if(len === k) {
            res.push(Array.from(path));
            return;
        }
        for(let a = i; a <= n + len - k + 1; a++) {
            path.push(a);
            backtracking(n, k, a + 1);
            path.pop();
        }
    }
};
//84ms
//45MB

二、电话号码的字母组合

1.题目：给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

示例:

输入：“23”
输出：[“ad”, “ae”, “af”, “bd”, “be”, “bf”, “cd”, “ce”, “cf”].
说明：尽管上面的答案是按字典序排列的，但是你可以任意选择答案输出的顺序。

2.解题思路：

var letterCombinations = function(digits) {
    const k = digits.length;
    const map = ["","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"];
    if(!k) return [];
    if(k === 1) return map[digits].split("");

    const res = [], path = [];
    backtracking(digits, k, 0);
    return res;

    function backtracking(n, k, a) {
        if(path.length === k) {
            res.push(path.join(""));
            return;
        }
        for(const v of map[n[a]]) {
            path.push(v);
            backtracking(n, k, a + 1);
            path.pop();
        }
    }
};
//64ms
//41.1MB

三、组合总和

1.题目：给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的数字可以无限制重复被选取。

说明：

所有数字（包括 target）都是正整数。
解集不能包含重复的组合。
示例 1：

输入：candidates = [2,3,6,7], target = 7,
所求解集为： [ [7], [2,2,3] ]
示例 2：

输入：candidates = [2,3,5], target = 8,
所求解集为： [ [2,2,2,2], [2,3,3], [3,5] ]

2.解题思路：

var combinationSum = function(candidates, target) {
    const res = [], path = [];
    candidates.sort((a,b)=>a-b); // 排序
    backtracking(0, 0);
    return res;
    function backtracking(j, sum) {
        if (sum === target) {
            res.push(Array.from(path));
            return;
        }
        for(let i = j; i < candidates.length; i++ ) {
            const n = candidates[i];
            if(n > target - sum) break;
            path.push(n);
            sum += n;
            backtracking(i, sum);
            path.pop();
            sum -= n;
        }
    }
};
//76ms
//44.6M

四、组合Ⅱ

1.题目：给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次。

说明： 所有数字（包括目标数）都是正整数。解集不能包含重复的组合。

示例 1:
输入: candidates = [10,1,2,7,6,1,5], target = 8,
所求解集为:
[
[1, 7],
[1, 2, 5],
[2, 6],
[1, 1, 6]
]
示例 2:
输入: candidates = [2,5,2,1,2], target = 5,
所求解集为:
[
[1,2,2],
[5]
]

2.解题思路：

/**
 * @param {number[]} candidates
 * @param {number} target
 * @return {number[][]}
 */
var combinationSum2 = function(candidates, target) {
    const res = [], path = [], len = candidates.length;
    candidates.sort((a,b)=>a-b);
    backtracking(0, 0);
    return res;
    function backtracking(sum, i) {
        if (sum === target) {
            res.push(Array.from(path));
            return;
        }
        for(let j = i; j < len; j++) {
            const n = candidates[j];
            if(j > i && candidates[j] === candidates[j-1]){
              //若当前元素和前一个元素相等
              //则本次循环结束，防止出现重复组合
              continue;
            }
            //如果当前元素值大于目标值-总和的值
            //由于数组已排序，那么该元素之后的元素必定不满足条件
            //直接终止当前层的递归
            if(n > target - sum) break;
            path.push(n);
            sum += n;
            backtracking(sum, j + 1);
            path.pop();
            sum -= n;
        }
    }
};

// 使用used去重（树层去重）
var combinationSum2 = function(candidates, target) {
    let res = [];
    let path = [];
    let total = 0;
    const len = candidates.length;
    candidates.sort((a, b) => a - b);
    let used = new Array(len).fill(false);
    const backtracking = (startIndex) => {
        if (total === target) {
            res.push([...path]);
            return;
        }
        for(let i = startIndex; i < len && total < target; i++) {
            const cur = candidates[i];
            if (cur > target - total || (i > 0 && cur === candidates[i - 1] && !used[i - 1])) continue;
            path.push(cur);
            total += cur;
            used[i] = true;
            backtracking(i + 1);
            path.pop();
            total -= cur;
            used[i] = false;
        }
    }
    backtracking(0);
    return res;
};

五、组合Ⅲ

1.题目
找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数，并且每种组合中不存在重复的数字。

说明：

所有数字都是正整数。
解集不能包含重复的组合。
示例 1: 输入: k = 3, n = 7 输出: [[1,2,4]]

示例 2: 输入: k = 3, n = 9 输出: [[1,2,6], [1,3,5], [2,3,4]]

2.**解题思路**：

```javascript
/**
 * @param {number} k
 * @param {number} n
 * @return {number[][]}
 */
var combinationSum3 = function(k, n) {
    let res = [];
    let path = [];
    let sum = 0;
    const dfs = (path,index) => {
        // 剪枝操作
        if (sum > n){
            return
        }
        if (path.length == k) {
            if(sum == n){
                res.push([...path]);
                return
            }
        }
        for (let i = index; i <= 9 - (k-path.length) + 1;i++) {
            path.push(i);
            sum = sum + i;
            index += 1;
            dfs(path,index);
            sum -= i
            path.pop()
        }
    }
    dfs(path,1);
    return res
};
// 56ms
// 41.4MB

六、分割回文串

1.题目：
给定一个字符串 s，将 s 分割成一些子串，使每个子串都是回文串。

返回 s 所有可能的分割方案。

示例: 输入: “aab” 输出: [ [“aa”,“b”], [“a”,“a”,“b”] ]
2.解题思路：

/**
 * @param {string} s
 * @return {string[][]}
 */
const isPalindrome = (s, l, r) => {
    for (let i = l, j = r; i < j; i++, j--) {
        if(s[i] !== s[j]) return false;
    }
    return true;
}

var partition = function(s) {
    const res = [], path = [], len = s.length;
    backtracking(0);
    return res;
    function backtracking(startIndex) {
        if(startIndex >= len) {
            res.push(Array.from(path));
            return;
        }
        for(let i = startIndex; i < len; i++) {
            if(!isPalindrome(s, startIndex, i)) continue;
            path.push(s.slice(startIndex, i + 1));
            backtracking(i + 1);
            path.pop();
        }
    }
};
// 224ms
// 60.4MB

七、复原IP地址

1.题目：
给定一个只包含数字的字符串，复原它并返回所有可能的 IP 地址格式。

有效的 IP 地址 正好由四个整数（每个整数位于 0 到 255 之间组成，且不能含有前导 0），整数之间用 ‘.’ 分隔。

例如：“0.1.2.201” 和 “192.168.1.1” 是 有效的 IP 地址，但是 “0.011.255.245”、“192.168.1.312” 和 “192.168@1.1” 是 无效的 IP 地址。

示例 1：
输入：s = “25525511135”
输出：[“255.255.11.135”,“255.255.111.35”]

示例 2：
输入：s = “0000”
输出：[“0.0.0.0”]

示例 3：
输入：s = “1111”
输出：[“1.1.1.1”]

示例 4：
输入：s = “010010”
输出：[“0.10.0.10”,“0.100.1.0”]

示例 5：
输入：s = “101023”
输出：[“1.0.10.23”,“1.0.102.3”,“10.1.0.23”,“10.10.2.3”,“101.0.2.3”]

提示：
0 <= s.length <= 3000
s 仅由数字组成

/**
 * @param {string} s
 * @return {string[]}
 */
var restoreIpAddresses = function(s) {
    const res = [], path = [];
    backtracking(0)
    return res;
    function backtracking(i) {
        const len = path.length;
        if(len > 4) return;
        if(len === 4 && i === s.length) {
            res.push(path.join("."));
            return;
        }
        for(let j = i; j < s.length; j++) {
            const str = s.slice(i, j + 1);
            if(str.length > 3 || +str > 255) break;
            if(str.length > 1 && str[0] === "0") break;
            path.push(str);
            backtracking(j + 1);
            path.pop()
        }
    }
};

八、子集问题

1.题目：
给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

示例: 输入: nums = [1,2,3] 输出: [ [3], [1], [2], [1,2,3], [1,3], [2,3], [1,2], [] ]

var subsets = function(nums) {
    let result = []
    let path = []
    function backtracking(startIndex) {
        result.push([...path])
        for(let i = startIndex; i < nums.length; i++) {
            path.push(nums[i])
            backtracking(i + 1)
            path.pop()
        }
    }
    backtracking(0)
    return result
};

九、子集Ⅱ

1.题目：
给定一个可能包含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

示例:
输入: [1,2,2]
输出: [ [2], [1], [1,2,2], [2,2], [1,2], [] ]

var subsetsWithDup = function(nums) {
    let result = []
    let path = []
    let sortNums = nums.sort((a, b) => {
        return a - b
    })
    function backtracing(startIndex, sortNums) {
        result.push([...path])
        if(startIndex > nums.length - 1) {
            return
        }
        for(let i = startIndex; i < nums.length; i++) {
            if(i > startIndex && nums[i] === nums[i - 1]) {
                continue
            }
            path.push(nums[i])
            backtracing(i + 1, sortNums)
            path.pop()
        }
    }
    backtracing(0, sortNums)
    return result
};
// 64ms
// 43MB

十、递增子序列

1.题目：
给定一个整型数组, 你的任务是找到所有该数组的递增子序列，递增子序列的长度至少是2。

示例:
输入: [4, 6, 7, 7]
输出: [[4, 6], [4, 7], [4, 6, 7], [4, 6, 7, 7], [6, 7], [6, 7, 7], [7,7], [4,7,7]]

说明:
给定数组的长度不会超过15。
数组中的整数范围是 [-100,100]。
给定数组中可能包含重复数字，相等的数字应该被视为递增的一种情况。

var findSubsequences = function(nums) {
    let result = []
    let path = []
    function backtracing(startIndex) {
        if(path.length > 1) {
            result.push(path.slice())
        }
        let uset = []
        for(let i = startIndex; i < nums.length; i++) {
            if((path.length > 0 && nums[i] < path[path.length - 1]) || uset[nums[i] + 100]) {
                continue
            }
            uset[nums[i] + 100] = true
            path.push(nums[i])
            backtracing(i + 1)
            path.pop()
        }
    }
    backtracing(0)
    return result
};
// 136ms
// 57.3MB

十一、重新安排行程

1.题目：
给定一个机票的字符串二维数组 [from, to]，子数组中的两个成员分别表示飞机出发和降落的机场地点，对该行程进行重新规划排序。所有这些机票都属于一个从 JFK（肯尼迪国际机场）出发的先生，所以该行程必须从 JFK 开始。

提示：
如果存在多种有效的行程，请你按字符自然排序返回最小的行程组合。例如，行程 [“JFK”, “LGA”] 与 [“JFK”, “LGB”] 相比就更小，排序更靠前
所有的机场都用三个大写字母表示（机场代码）。
假定所有机票至少存在一种合理的行程。
所有的机票必须都用一次 且 只能用一次。

示例 1：
输入：[[“MUC”, “LHR”], [“JFK”, “MUC”], [“SFO”, “SJC”], [“LHR”, “SFO”]]
输出：[“JFK”, “MUC”, “LHR”, “SFO”, “SJC”]

示例 2：
输入：[[“JFK”,“SFO”],[“JFK”,“ATL”],[“SFO”,“ATL”],[“ATL”,“JFK”],[“ATL”,“SFO”]]
输出：[“JFK”,“ATL”,“JFK”,“SFO”,“ATL”,“SFO”]
解释：另一种有效的行程是 [“JFK”,“SFO”,“ATL”,“JFK”,“ATL”,“SFO”]。但是它自然排序更大更靠后

var findItinerary = function(tickets) {
    let result = ['JFK']
    let map = {}

    for (const tickt of tickets) {
        const [from, to] = tickt
        if (!map[from]) {
            map[from] = []
        }
        map[from].push(to)
    }

    for (const city in map) {
        // 对到达城市列表排序
        map[city].sort()
    }
    function backtracing() {
        if (result.length === tickets.length + 1) {
            return true
        }
        if (!map[result[result.length - 1]] || !map[result[result.length - 1]].length) {
            return false
        }
        for(let i = 0 ; i <  map[result[result.length - 1]].length; i++) {
            let city = map[result[result.length - 1]][i]
            // 删除已走过航线，防止死循环
            map[result[result.length - 1]].splice(i, 1)
            result.push(city)
            if (backtracing()) {
                return true
            }
            result.pop()
            map[result[result.length - 1]].splice(i, 0, city)
        }
    }
    backtracing()
    return result
};
// 84ms
// 47.5MB

十二、全排列

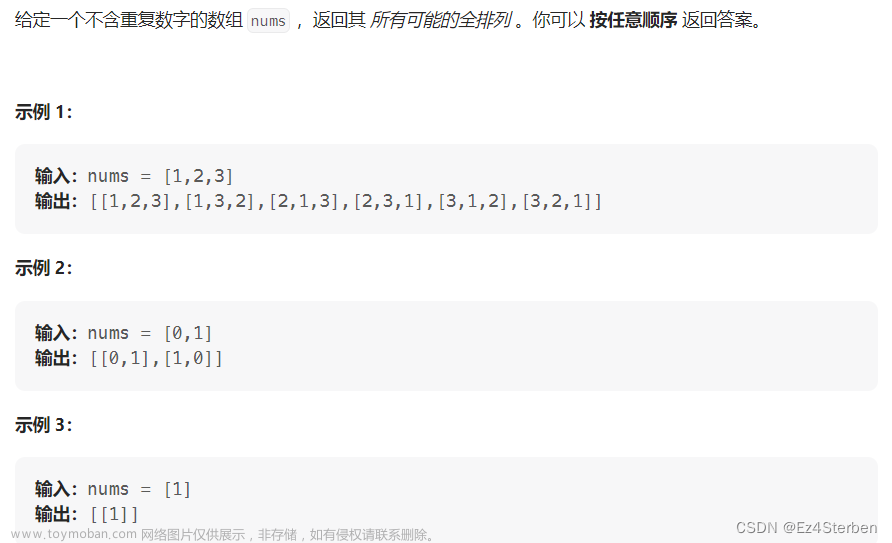
1.题目：
给定一个 没有重复 数字的序列，返回其所有可能的全排列。

示例:

输入: [1,2,3]
输出: [ [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1] ]

/**
 * @param {number[]} nums
 * @return {number[][]}
 */
var permute = function(nums) {
    const res = [], path = [];
    backtracking(nums, nums.length, []);
    return res;
    
    function backtracking(n, k, used) {
        if(path.length === k) {
            res.push(Array.from(path));
            return;
        }
        for (let i = 0; i < k; i++ ) {
            if(used[i]) continue;
            path.push(n[i]);
            used[i] = true; // 同支
            backtracking(n, k, used);
            path.pop();
            used[i] = false;
        }
    }
};
// 80ms
// 44.7MB

十三、全排列Ⅱ

1.题目：
给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

示例 1：
输入：nums = [1,1,2]
输出： [[1,1,2], [1,2,1], [2,1,1]]

示例 2：
输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

提示：
1 <= nums.length <= 8
-10 <= nums[i] <= 10

var permuteUnique = function (nums) {
    nums.sort((a, b) => {
        return a - b
    })
    let result = []
    let path = []

    function backtracing( used) {
        if (path.length === nums.length) {
            result.push([...path])
            return
        }
        for (let i = 0; i < nums.length; i++) {
            if (i > 0 && nums[i] === nums[i - 1] && !used[i - 1]) {
                continue
            }
            if (!used[i]) {
                used[i] = true
                path.push(nums[i])
                backtracing(used)
                path.pop()
                used[i] = false
            }


        }
    }
    backtracing([])
    return result
};
// 72ms
// 43.8MB

十四、N皇后

1.题目：
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。

示例 1：

var solveNQueens = function(n) {
    function isValid(row, col, chessBoard, n) {

        for(let i = 0; i < row; i++) {
            if(chessBoard[i][col] === 'Q') {
                return false
            }
        }

        for(let i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
            if(chessBoard[i][j] === 'Q') {
                return false
            }
        }

        for(let i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
            if(chessBoard[i][j] === 'Q') {
                return false
            }
        }
        return true
    }

    function transformChessBoard(chessBoard) {
        let chessBoardBack = []
        chessBoard.forEach(row => {
            let rowStr = ''
            row.forEach(value => {
                rowStr += value
            })
            chessBoardBack.push(rowStr)
        })

        return chessBoardBack
    }

    let result = []
    function backtracing(row,chessBoard) {
        if(row === n) {
            result.push(transformChessBoard(chessBoard))
            return
        }
        for(let col = 0; col < n; col++) {
            if(isValid(row, col, chessBoard, n)) {
                chessBoard[row][col] = 'Q'
                backtracing(row + 1,chessBoard)
                chessBoard[row][col] = '.'
            }
        }
    }
    let chessBoard = new Array(n).fill([]).map(() => new Array(n).fill('.'))
    backtracing(0,chessBoard)
    return result
    
};
// 88ms
// 44.3MB

十五、解数独

1.题目：
编写一个程序，通过填充空格来解决数独问题。

一个数独的解法需遵循如下规则： 数字 1-9 在每一行只能出现一次。 数字 1-9 在每一列只能出现一次。 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。 空白格用 ‘.’ 表示。

提示：
给定的数独序列只包含数字 1-9 和字符 ‘.’ 。
你可以假设给定的数独只有唯一解。
给定数独永远是 9x9 形式的。

var solveSudoku = function(board) {
    function isValid(row, col, val, board) {
        let len = board.length
        // 行不能重复
        for(let i = 0; i < len; i++) {
            if(board[row][i] === val) {
                return false
            }
        }
        // 列不能重复
        for(let i = 0; i < len; i++) {
            if(board[i][col] === val) {
                return false
            }
        }
        let startRow = Math.floor(row / 3) * 3
        let startCol = Math.floor(col / 3) * 3

        for(let i = startRow; i < startRow + 3; i++) {
            for(let j = startCol; j < startCol + 3; j++) {
                if(board[i][j] === val) {
                    return false
                }
            }
        }

        return true
    }

    function backTracking(board) {
        for(let i = 0; i < board.length; i++) {
            for(let j = 0; j < board[0].length; j++) {
                if(board[i][j] !== '.') continue
                for(let val = 1; val <= 9; val++) {
                    if(isValid(i, j, `${val}`, board)) {
                        board[i][j] = `${val}`
                        if (backTracking()) {
                            return true
                        }

                        board[i][j] = `.`
                    }
                }
                return false
            }
        }
        return true
    }
    backTracking(board)
    return board

};
// 104ms
// 42MB

十六、回溯算法去重问题的另一种写法

1.题目：文章来源地址https://www.toymoban.com/news/detail-426787.html

到了这里，关于初级算法-回溯算法的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！