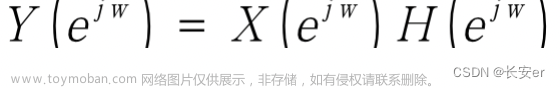信号处理的目的是从噪声中提取信号,得到不受干扰影响的真正信号。采用的处理系统称为滤波器。
实时信号处理中,希望滤波器的参数可以根据系统或环境的变化进行更新,称为自适应滤波器。

滤波器的分类:
线性滤波器、非线性滤波器;
FIR滤波器、IIR滤波器;
时域滤波器、频域滤波器、空域滤波器;
最优滤波:
所谓最优是在某种标准下系统性能达到最佳。
相对性:在某种准则下的最优系统,在另外一种准则下就不一定是最优的。
等价性:在某些特定条件下,几种最优准则也可能是等价的。
最优线性滤波器的设计准则:
滤波器输出信噪比在某一特定时刻达到最大,称为匹配滤波器;
滤波器输出的信号波形与发送信号波形之间的均方误差最小,称为维纳滤波器。
匹配滤波器:

滤波器输出噪声的平均功率为

在抽样时刻t0,线性滤波器输出信号的瞬时功率与噪声平均功率之比为

施瓦兹(Schwartz)不等式

式中,X(w)和Y(w)都是实变量ω的复函数。当且仅当
X(w)=KY*(w)
时式中等式才能成立。





即匹配滤波器的单位冲激响应为
h(t)=s(t0-t)
上式表明,匹配滤波器的单位冲激响应h(t)是输入信号s(t)的镜像函数,t0为输出最大信噪比时刻。


上式条件说明,对于一个物理可实现的匹配滤波器,其输入信号s(t)必须在它输出最大信噪比的时刻t0之前结束,也就是说,若输入信号在T时刻结束,则对物理可实现的匹配滤波器,其输出最大信噪比时刻t0必须在输入信号结束之后,即t0≥T。对于接收机来说,t0是时间延迟,通常总是希望时间延迟尽可能小,因此一般情况可取t0=T。

上式表明,匹配滤波器的输出波形是输入信号s(t)的自相关函数。因此,匹配滤波器可以看成是一个计算输入信号自相关函数的相关器,其在t0时刻得到最大输出信噪比。







匹配滤波器输出信号无论是在时域还是在频域,其波形都是杂乱无章,因此判断输入信号只有噪声,没有有用的信号。



匹配滤波器输出信号的幅度小于设置的门限,因此判断接收信号没有我们所关心的目标。

参考视频:文章来源:https://www.toymoban.com/news/detail-426801.html
https://www.bilibili.com/video/BV1wS4y1D7ng?p=7&vd_source=77c874a500ef21df351103560dada737文章来源地址https://www.toymoban.com/news/detail-426801.html
到了这里,关于现代信号处理——自适应滤波器(匹配滤波器)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!