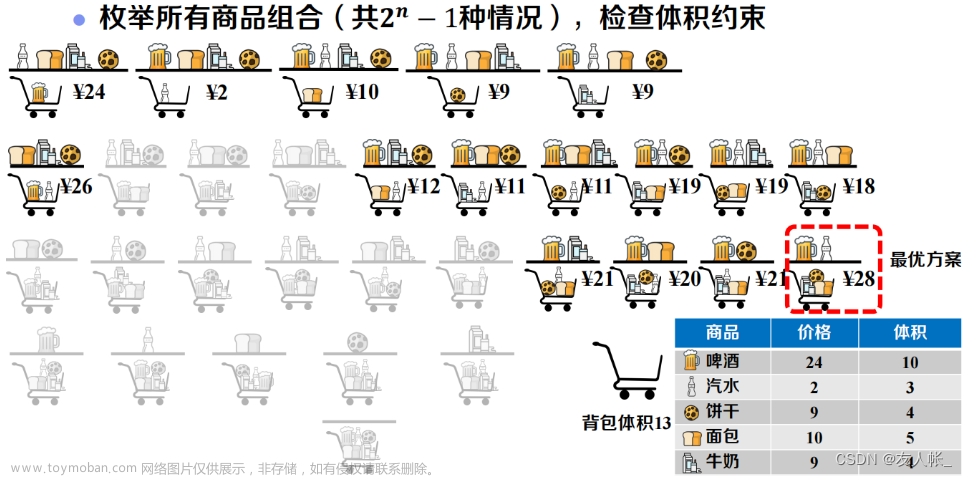
java实现0-1背包问题方案(动态规划-贪心算法-回溯-分支定界)-Toy模板网

这篇具有很好参考价值的文章主要介绍了java实现0-1背包问题方案(动态规划-贪心算法-回溯-分支定界)。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

java实现0-1背包问题方案(动态规划-贪心算法-回溯-分支定界)

算法实现说明

动态规划算法时间复杂度较低，能够求解较大规模的问题，但空间复杂度较高，不适用于数据量较大的问题。
贪心算法时间复杂度较低，能够求解较大规模的问题，但不能保证求得的解是最优解。
回溯算法能够求解较小规模的问题，但时间复杂度较高，不适用于数据量较大的问题。
分支定界算法能够求解较小规模的问题，但时间复杂度较高，不适用于数据量较大的问题。

0-1背包问题说明

0-1背包问题是一个经典的组合优化问题，其问题描述如下：

有一个容量为 $C$ 的背包，和 $n$ 个物品，每个物品有重量 $w_i$ 和价值 $v_i$ ，现在需要从这 $n$ 个物品中选择一些物品放入背包中，使得这些物品的总重量不超过 $C$ ，且这些物品的总价值最大。

0-1背包问题是一个 NP 完全问题，因此不存在多项式时间复杂度的算法能够求解该问题。但是，我们可以使用多种算法来求解该问题，包括动态规划、贪心、回溯、分支定界算法等。

动态规划算法

动态规划算法是求解0-1背包问题的一种常用算法，其时间复杂度较低，能够求解较大规模的问题。动态规划算法的基本思想是将原问题分解为若干个子问题，先求解子问题，再由子问题的解得到原问题的解。

动态规划算法求解0-1背包问题的时间复杂度为 $O (n * c)$ ，空间复杂度为 $O (n * c)$ ，其中 $n$ 表示物品的数量， $c$ 表示背包的容量。

 /**
     * 动态规划求解0-1背包问题
     * @param w 物品重量
     * @param v 物品价值
     * @param c 背包容量
     * @return 背包能装下的最大价值
     * 时间复杂度：O(n*c)
     * 空间复杂度：O(n*c)
     * 优点：时间复杂度较低，能够求解较大规模的问题
     * 缺点：空间复杂度较高，不适用于数据量较大的问题
     */
    public static int knapsack(int[] w, int[] v, int c) {
        int n = w.length;
        int[][] dp = new int[n + 1][c + 1];
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= c; j++) {
                if (j < w[i - 1]) {
                    // 背包容量不足，不能装入第i个物品
                    dp[i][j] = dp[i - 1][j];
                } else {
                    // 能装入第i个物品
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - w[i - 1]] + v[i - 1]);
                }
            }
        }
        // 返回背包能装下的最大价值
        return dp[n][c];
    }

贪心算法

贪心算法是求解0-1背包问题的一种常用算法，其时间复杂度较低，能够求解较大规模的问题。贪心算法的基本思想是每次选择当前最优的解，直到得到最终的解。

贪心算法求解0-1背包问题的时间复杂度为 $O (n * l o g (n))$ ，空间复杂度为 $O (n)$ 。

   /**
     * 贪心算法求解0-1背包问题
     * @param w 物品重量
     * @param v 物品价值
     * @param c 背包容量
     * @return 背包能装下的最大价值
     * 时间复杂度：O(n*log(n))
     * 空间复杂度：O(n)
     * 优点：时间复杂度较低，能够求解较大规模的问题
     * 缺点：不能保证求得的是最优解，只能得到一个近似解
     */
    public static int greedyKnapsack(int[] w, int[] v, int c) {
        int n = w.length;
        int[] index = new int[n];
        for (int i = 0; i < n; i++) {
            index[i] = i;
        }
        int[] temp = new int[n];
        for (int i = 0; i < n; i++) {
            temp[i] = v[i] * w[i];
        }
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                if (temp[i] < temp[j]) {
                    int t = temp[i];
                    temp[i] = temp[j];
                    temp[j] = t;
                    t = index[i];
                    index[i] = index[j];
                    index[j] = t;
                }
            }
        }
        int maxValue = 0;
        for (int i = 0; i < n; i++) {
            if (w[index[i]] <= c) {
                maxValue += v[index[i]];
                c -= w[index[i]];
            } else {
                maxValue += (int) ((double) v[index[i]] / w[index[i]] * c);
                break;
            }
        }
        return maxValue;
    }

回溯算法

回溯算法是求解0-1背包问题的一种常用算法，其能够求解较小规模的问题。回溯算法的基本思想是搜索所有可能的解，找到最优解。

回溯算法求解0-1背包问题的时间复杂度为 $O(2^n)$ ，空间复杂度为 $O (n)$ 。

   /**
     * 回溯算法求解0-1背包问题
     * @param w 物品重量
     * @param v 物品价值
     * @param c 背包容量
     * @return 背包能装下的最大价值
     * 时间复杂度：O(2^n)
     * 空间复杂度：O(n)
     * 优点：能够求解较小规模的问题
     * 缺点：时间复杂度较高，不适用于数据量较大的问题
     */
    public static int backtrackKnapsack(int[] w, int[] v, int c) {
        int n = w.length;
        int maxValue = 0;
        for (int i = 0; i < (1 << n); i++) {
            int currentWeight = 0;
            int currentValue = 0;
            for (int j = 0; j < n; j++) {
                if ((i & (1 << j)) != 0) {
                    currentWeight += w[j];
                    currentValue += v[j];
                }
            }
            if (currentWeight <= c && currentValue > maxValue) {
                maxValue = currentValue;
            }
        }
        return maxValue;
    }

分支定界算法

分支定界算法是求解0-1背包问题的一种常用算法，其能够求解较小规模的问题。分支定界算法的基本思想是搜索所有可能的解，但是在搜索过程中，通过一些限制条件，剪枝掉一些不可能成为最优解的分支，从而减少搜索的时间。

分支定界算法求解0-1背包问题的时间复杂度为 $O(2^n)$ ，空间复杂度为 $O (n)$ 。文章来源地址https://www.toymoban.com/news/detail-427145.html

   /**
     * 分支定界算法求解0-1背包问题
     * @param w 物品重量
     * @param v 物品价值
     * @param c 背包容量
     * @return 背包能装下的最大价值
     * 时间复杂度：O(2^n)
     * 空间复杂度：O(n)
     * 优点：能够求解较小规模的问题
     * 缺点：时间复杂度较高，不适用于数据量较大的问题
     */
    public static int branchBoundKnapsack(int[] w, int[] v, int c) {
        int n = w.length;
        int[] index = new int[n];
        for (int i = 0; i < n; i++) {
            index[i] = i;
        }
        int[] temp = new int[n];
        for (int i = 0; i < n; i++) {
            temp[i] = v[i] * w[i];
        }
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                if (temp[i] < temp[j]) {
                    int t = temp[i];
                    temp[i] = temp[j];
                    temp[j] = t;
                    t = index[i];
                    index[i] = index[j];
                    index[j] = t;
                }
            }
        }
        int maxValue = 0;
        int currentValue = 0;
        int currentWeight = 0;
        int i = 0;
        while (i >= 0) {
            if (i == n) {
                if (currentValue > maxValue) {
                    maxValue = currentValue;
                }
                i--;
            } else if (currentWeight + w[index[i]] <= c) {
                currentWeight += w[index[i]];
                currentValue += v[index[i]];
                i++;
            } else {
                i--;
            }
            if (i >= n || i < 0 || index[i] >= n || currentWeight + w[index[i]] > c || currentValue + (c - currentWeight) * (double) v[index[i]] / w[index[i]] <= maxValue) {
                i--;
            }
        }
        return maxValue;
    }

算法汇总代码



/**
 * 代码实现:
 * 动态规划算法时间复杂度较低，能够求解较大规模的问题，但空间复杂度较高，不适用于数据量较大的问题。
 * 贪心算法时间复杂度较低，能够求解较大规模的问题，但不能保证求得的解是最优解。
 * 回溯算法能够求解较小规模的问题，但时间复杂度较高，不适用于数据量较大的问题。
 * 分支定界算法能够求解较小规模的问题，但时间复杂度较高，不适用于数据量较大的问题。
 */
import java.util.Arrays;

public class KnapsackTest {
    public static void main(String[] args) {
        // 物品重量
        int[] w = {2, 4, 6, 8, 9, 2, 4, 6, 8, 9, 2, 4, 6, 8, 9, 2, 4, 6, 8, 9};
        // 物品价值
        int[] v = {1, 3, 5, 7, 9, 1, 3, 5, 7, 9, 1, 3, 5, 7, 9, 1, 3, 5, 7, 9};
        // 背包容量1
        int c1 = 10;
        // 背包容量2
        int c2 = 100;
        long startTime1 = System.nanoTime();
        int[] result1 = {knapsack(w, v, c1)};
        long endTime1 = System.nanoTime();
        long duration1 = (endTime1 - startTime1);
        long startTime2 = System.nanoTime();
        int[] result2 = {knapsack(w, v, c2)};
        long endTime2 = System.nanoTime();
        long duration2 = (endTime2 - startTime2);
        System.out.println("当背包容量为10时，动态规划算法的结果为：" + result1[0] + "，执行时间为：" + duration1 + "纳秒");
        System.out.println("当背包容量为10时，贪心算法的结果为：" + greedyKnapsack(w, v, c1) + "，执行时间为：" + (System.nanoTime() - endTime1) + "纳秒");
        System.out.println("当背包容量为10时，回溯算法的结果为：" + backtrackKnapsack(w, v, c1) + "，执行时间为：" + (System.nanoTime() - endTime1) + "纳秒");
        System.out.println("当背包容量为10时，分支定界算法的结果为：" + branchBoundKnapsack(w, v, c1) + "，执行时间为：" + (System.nanoTime() - endTime1) + "纳秒");
        System.out.println("当背包容量为100时，动态规划算法的结果为：" + result2[0] + "，执行时间为：" + duration2 + "纳秒");
        System.out.println("当背包容量为100时，贪心算法的结果为：" + greedyKnapsack(w, v, c2) + "，执行时间为：" + (System.nanoTime() - endTime2) + "纳秒");
        System.out.println("当背包容量为100时，回溯算法的结果为：" + backtrackKnapsack(w, v, c2) + "，执行时间为：" + (System.nanoTime() - endTime2) + "纳秒");
        System.out.println("当背包容量为100时，分支定界算法的结果为：" + branchBoundKnapsack(w, v, c2) + "，执行时间为：" + (System.nanoTime() - endTime2) + "纳秒");
    }

    /**
     * 动态规划求解0-1背包问题
     * @param w 物品重量
     * @param v 物品价值
     * @param c 背包容量
     * @return 背包能装下的最大价值
     * 时间复杂度：O(n*c)
     * 空间复杂度：O(n*c)
     * 优点：时间复杂度较低，能够求解较大规模的问题
     * 缺点：空间复杂度较高，不适用于数据量较大的问题
     */
    public static int knapsack(int[] w, int[] v, int c) {
        int n = w.length;
        int[][] dp = new int[n + 1][c + 1];
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= c; j++) {
                if (j < w[i - 1]) {
                    // 背包容量不足，不能装入第i个物品
                    dp[i][j] = dp[i - 1][j];
                } else {
                    // 能装入第i个物品
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - w[i - 1]] + v[i - 1]);
                }
            }
        }
        // 返回背包能装下的最大价值
        return dp[n][c];
    }

    /**
     * 贪心算法求解0-1背包问题
     * @param w 物品重量
     * @param v 物品价值
     * @param c 背包容量
     * @return 背包能装下的最大价值
     * 时间复杂度：O(n*log(n))
     * 空间复杂度：O(n)
     * 优点：时间复杂度较低，能够求解较大规模的问题
     * 缺点：不能保证求得的是最优解，只能得到一个近似解
     */
    public static int greedyKnapsack(int[] w, int[] v, int c) {
        int n = w.length;
        int[] index = new int[n];
        for (int i = 0; i < n; i++) {
            index[i] = i;
        }
        int[] temp = new int[n];
        for (int i = 0; i < n; i++) {
            temp[i] = v[i] * w[i];
        }
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                if (temp[i] < temp[j]) {
                    int t = temp[i];
                    temp[i] = temp[j];
                    temp[j] = t;
                    t = index[i];
                    index[i] = index[j];
                    index[j] = t;
                }
            }
        }
        int maxValue = 0;
        for (int i = 0; i < n; i++) {
            if (w[index[i]] <= c) {
                maxValue += v[index[i]];
                c -= w[index[i]];
            } else {
                maxValue += (int) ((double) v[index[i]] / w[index[i]] * c);
                break;
            }
        }
        return maxValue;
    }

    /**
     * 回溯算法求解0-1背包问题
     * @param w 物品重量
     * @param v 物品价值
     * @param c 背包容量
     * @return 背包能装下的最大价值
     * 时间复杂度：O(2^n)
     * 空间复杂度：O(n)
     * 优点：能够求解较小规模的问题
     * 缺点：时间复杂度较高，不适用于数据量较大的问题
     */
    public static int backtrackKnapsack(int[] w, int[] v, int c) {
        int n = w.length;
        int maxValue = 0;
        for (int i = 0; i < (1 << n); i++) {
            int currentWeight = 0;
            int currentValue = 0;
            for (int j = 0; j < n; j++) {
                if ((i & (1 << j)) != 0) {
                    currentWeight += w[j];
                    currentValue += v[j];
                }
            }
            if (currentWeight <= c && currentValue > maxValue) {
                maxValue = currentValue;
            }
        }
        return maxValue;
    }

    /**
     * 分支定界算法求解0-1背包问题
     * @param w 物品重量
     * @param v 物品价值
     * @param c 背包容量
     * @return 背包能装下的最大价值
     * 时间复杂度：O(2^n)
     * 空间复杂度：O(n)
     * 优点：能够求解较小规模的问题
     * 缺点：时间复杂度较高，不适用于数据量较大的问题
     */
    public static int branchBoundKnapsack(int[] w, int[] v, int c) {
        int n = w.length;
        int[] index = new int[n];
        for (int i = 0; i < n; i++) {
            index[i] = i;
        }
        int[] temp = new int[n];
        for (int i = 0; i < n; i++) {
            temp[i] = v[i] * w[i];
        }
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                if (temp[i] < temp[j]) {
                    int t = temp[i];
                    temp[i] = temp[j];
                    temp[j] = t;
                    t = index[i];
                    index[i] = index[j];
                    index[j] = t;
                }
            }
        }
        int maxValue = 0;
        int currentValue = 0;
        int currentWeight = 0;
        int i = 0;
        while (i >= 0) {
            if (i == n) {
                if (currentValue > maxValue) {
                    maxValue = currentValue;
                }
                i--;
            } else if (currentWeight + w[index[i]] <= c) {
                currentWeight += w[index[i]];
                currentValue += v[index[i]];
                i++;
            } else {
                i--;
            }
            if (i >= n || i < 0 || index[i] >= n || currentWeight + w[index[i]] > c || currentValue + (c - currentWeight) * (double) v[index[i]] / w[index[i]] <= maxValue) {
                i--;
            }
        }
        return maxValue;
    }
}